sparse.coo_matrix()

coo_matrix.tocsr（copy = False ）

将此矩阵转换为压缩稀疏行格式，重复的条目将汇总在一起。

举例：

from numpy import array
from scipy.sparse import coo_matrix
row  = array([0, 0, 1, 3, 1, 0, 0])
col  = array([0, 2, 1, 3, 1, 0, 0])
data = array([1, 1, 1, 1, 1, 1, 1])
A = coo_matrix((data, (row, col)), shape=(4, 4)).tocsr()
A.toarray()

　

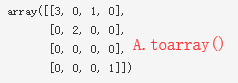
　　数组r中的元素和它对应下标的c列表中的元素组成了非零数字在稀疏矩阵中的坐标，r和c的第一个元素都是0，说明矩阵坐标(0,0)位置有非零数字，这个数字是几呢？这就要看data数组了。由于data的数值都是1，(0,0)出现两次，那么(0,0)位置的数值就是1+1=2。这里我们用r,c,data三个数组配合coo_matrix构造了一个稀疏矩阵。稀疏矩阵在计算机中的coo形式存储就是这个的逆过程。

　　在做特征工程的过程中，对于那些取值是多个类别的变量，经常要用到One-Hot编码，其结果就是得到稀疏矩阵X。现在要在数据集X的基础上加上一些做过一个列变量变换的数据集features,features不是稀疏矩阵，要合并X和feature就需要进行如下操作：

if sparse.issparse(X):     #判断X是否稀疏
	features = sparse.lil_matrix(features)    将features数据集用lil_matrix()稀疏化
	X = sparse.hstack((X, features), 'csr')   横向合并X和稀疏后的features,并存储为csr格式

　　

参考文献：

【1】Scipy_Sparse介绍