【算法】浅学 LCA

参考资料

浅析最近公共祖先（LCA）

最近公共祖先 - OI Wiki

【白话系列】倍增算法

一、概念

最近公共祖先称为 LCA （Lowest Common Ancestor）

它指的是在一颗树中，离两个节点最近的公共祖先

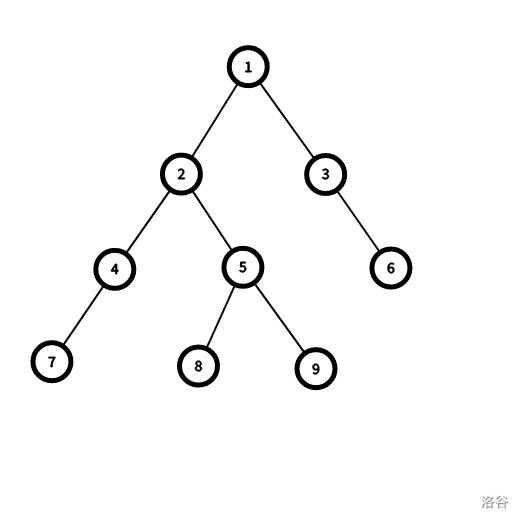
如下图，

节点 7 和节点 5 的最近公共祖先是 2

节点 8 和节点 3 的最近公共祖先是 1

节点 4 和节点 2 的最近公共祖先是 2

那么求 LCA 有哪些方法呢？

二、实现

• 暴力

我们不难想到一种很暴力的想法

如上图，现在我们要求 7 和 5 的 LCA

令 x = 7 , y = 5

首先我们先让 x 和 y 两个节点在同一层，如果深度不一的话，浅的那个节点很有可能就会超过他们的 LCA

x 变为它的父节点,通俗点说就是跳到它父节点的位置

现在 x 和 y 深度相等了，就一起跳到它们各自的父节点，直到 x 和 y 跳到了同一个节点。而这个节点就是它们的 LCA

很显然，时间爆掉了，我们需要一点优化

• 倍增

上面的想法一格一格地跳太慢了，那么可不可以让它们一次跳一大块呢？

这里我们就可以运用倍增思想，不了解倍增思想的可以先看看参考资料那

先定义几个数组

\(fa_{[i][j]}\) 表示 i 节点的第 \(2^j\) 个祖先

\(deep_{[i]}\) 表示 i 节点的深度

首先还是一样的，将 x 和 y 跳到同一深度，这里也要用倍增法

每次考虑跳 \(2^n\) 次，但是不能超过 LCA 的深度

也就是每次跳的时候，判定一下如果跳了 \(2^n\) 后，两个节点的父亲会不会相同，如果相同，就表示跳到 LCA 或者跳过头了

最后输出跳完之后 x 和 y 的父节点即可

预处理 fa 数组时，我们可以运用一个显而易见的结论，i 的 \(2^j\) 个祖先 = i 的 \(2^{j-1}\) 个祖先的 \(2^{j-1}\) 个祖先

表示出来就是这样的：

\[fa[i][j]=fa[fa[i][j-1]][j-1];
\]

为什么呢？

首先不难得出，\(2^{j-1}=2^j\div2\) (初中的幂运算）

这在树上可以表现为将 i 上面的 \(2^j\) 层平均分成了两份，跳了一半，再跳一半，当然就可以跳到层的最顶端了

三、代码

• 暴力

• 倍增

#include<bits/stdc++.h>
using namespace std;

const int N=5e5+5;
int n,m,s;
int tot,head[N<<1];
int ln,fa[N][35],deep[N];

struct node{
	int nex,to;
}edge[N<<1];

void add(int x,int y){
	edge[++tot].to=y;
	edge[tot].nex=head[x];
	head[x]=tot;
}

void dfs(int x,int fx){
	fa[x][0]=fx;
	deep[x]=deep[fx]+1;
	for(int i=1;i<=ln;i++){
		fa[x][i]=fa[fa[x][i-1]][i-1];
	}
	for(int i=head[x];i;i=edge[i].nex){
		if(edge[i].to==fx) continue;
		dfs(edge[i].to,x);
	}
}

int lca(int x,int y){
	if(deep[x]>deep[y]) swap(x,y);
	for(int i=ln;i>=0;i--){
		if((deep[y]-deep[x])>>i&1!=0) y=fa[y][i];
	}
	if(x==y) return x;
	for(int i=ln;i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			x=fa[x][i];y=fa[y][i];
		}
	}
	return fa[x][0];
}

int main(){
	ios::sync_with_stdio(false);
	cin>>n>>m>>s;
	ln=log2(n);
	for(int i=1;i<=n-1;i++){
		int x,y;
		cin>>x>>y;
		add(x,y);add(y,x);
	}
	dfs(s,0);
	for(int i=1;i<=m;i++){
		int x,y;
		cin>>x>>y;
		cout<<lca(x,y)<<"\n";
	}
	return 0;
}

四、时间复杂度

• 暴力

操作	时间复杂度
预处理	O(n)
查询	O(n)
随机树查询	O(log n)

• 倍增

操作	时间复杂度
预处理	O(n log n)
查询	O(log n)

五、例题

• 斐波那契

problem

Solve

看到题面，一眼 LCA

但这颗树和普通的树不一样，关键在于它编码之间的父子关系，所以我们不妨先观察一下这颗树：

看一下父子节点之间的差值（以 1 和它的孩子们为例）

孩子	差值
2	1
3	2
4	3
6	5
9	8

如果还是没能看出规律的话，不妨在最前面加一个 1，数列就变成了 1 1 2 3 5 8，这就是斐波那契数列

于是我们可以通过这个关系来找到子节点的父亲，与 LCA 的算法思想一样，假设现在要求 x 和 y 两个节点的 LCA

如果 x = y，就意味着它们已经找到了最近公告祖先，直接跳出循环

否则找到 x，y中编号更大的一个，跳到它的父节点

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N=3e5+50;
const int M=60;
int fli[N];

inline int lca(int x,int y){
	while(x!=y){
		if(x<y) swap(x,y);
		int l=0,r=M+1;
		while(l+1<r){
			int mid=(l+r)>>1;
			if(fli[mid]<x) l=mid;
			else r=mid;
		}
		x-=fli[l];
	}
	return x;
}

signed main(){
	ios::sync_with_stdio(false);
	int t;
	cin>>t;
	fli[1]=fli[2]=1;
	for(int i=3;i<=M;i++) fli[i]=fli[i-1]+fli[i-2];
	while(t--){
		int x,y;
		cin>>x>>y;
		cout<<lca(x,y)<<"\n";
	}
	return 0;
}

• 紧急集合

Problem

Solve

三个节点的最近公共祖先问题，可能会想到两两求最近公共祖先的想法，但其实这样路径并不会最小，比如下面这图，要求的三个点分别为5 7 8：

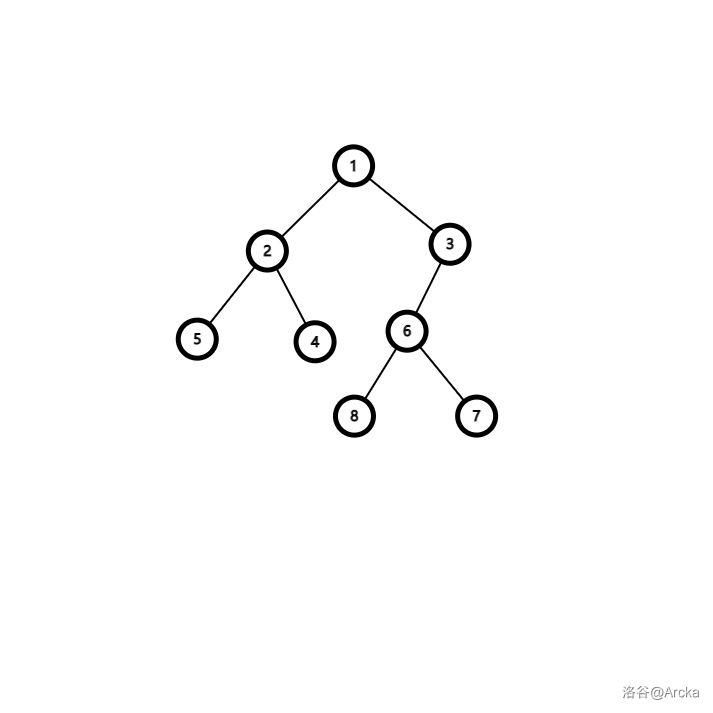
按照之前的思路，它们应该在 1 集合，此时的花费是 8。但如果在 6 集合的话，花费只有 6，明显更优

我们分别对三个点取 LCA，此时：

节点 A	节点 B	LCA
5	8	1
5	7	1
7	8	6

此时有两个 LCA 重合，而更优的是取不重合的那个节点，我们就可以就此写出代码了

Code

#include<bits/stdc++.h>
using namespace std;

const int N=5e5+5;
int n,ln;
int tot,head[N<<1];
int deep[N],fa[N][35];
int ansi,money;

struct node{
	int to,nxt;
}edge[N<<1];

void add(int x,int y){
	edge[++tot].to=y;
	edge[tot].nxt=head[x];
	head[x]=tot;
}

void dfs(int x,int fx){
	deep[x]=deep[fx]+1;
	fa[x][0]=fx;
	for(int i=1;i<=ln;i++) fa[x][i]=fa[fa[x][i-1]][i-1];
	for(int i=head[x];i;i=edge[i].nxt){
		int son=edge[i].to;
		if(son==fx) continue;
		dfs(son,x);
	}
}

int lca(int x,int y){
	if(deep[x]<deep[y]) swap(x,y);
	for(int i=ln;i>=0;i--){
		if(((deep[x]-deep[y])>>i&1)!=0){
			x=fa[x][i];
		//	money+=(1>>i);
		}
	}
	if(x==y) return x;
	for(int i=ln;i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			x=fa[x][i];y=fa[y][i];
		//	money+=(1<<i);
		}
	}
//	money++;
	return fa[x][0];
}

int main(){
	ios::sync_with_stdio(false);
	int t;
	cin>>n>>t;
	ln=log2(n);
	for(int i=1;i<n;i++){
		int x,y;
		cin>>x>>y;
		add(x,y);add(y,x);
	}
	dfs(1,0);
	while(t--){
		//money=0;
		int x,y,z,a,b,c;
		cin>>x>>y>>z;
	//	cout<<lca(lca(x,y),lca(y,z))<<" "<<money<<"\n";
		a=lca(x,y),b=lca(y,z),c=lca(x,z);
		if(a==b) ansi=c;
		else if(b==c) ansi=a;
		else ansi=b;
		money=deep[x]+deep[y]+deep[z]-deep[a]-deep[b]-deep[c];
		cout<<ansi<<" "<<money<<"\n";
	}
	return 0;
}