记一道经典树上Nim游戏

这道题首先是 Hanriver 提出来的，但是大家都不会做，今天看到了一道一模一样的题目 AT2667

题目大意是，每个人删掉一个不是整棵树的原树的子树，给定一个树问游戏状态。

首先，这是需要用到多个游戏与多个状态的定理得到的。但是很明显在此处直接使用定理会产生 \(\mathcal O(2^n)\) 的复杂度，那么应该怎么思考呢？

既然能做，那么有一些状态肯定是不必要进行的，也就是说需要计入 \(\text{mex}\) 的未必是所有的状态。回忆一下，计算 \(\text{SG}\) 值有两种方法:

1. 子状态的 \(\text{mex}\)
2. 子游戏的异或和
3. 一般是归纳证明的对于简单状态结论，或是递推式

如何考虑这道问题呢？当状态过多无法转移时，我们就想要把原来的状态分成若干个子游戏。果然，我们可以拆掉原来的树，像这样：

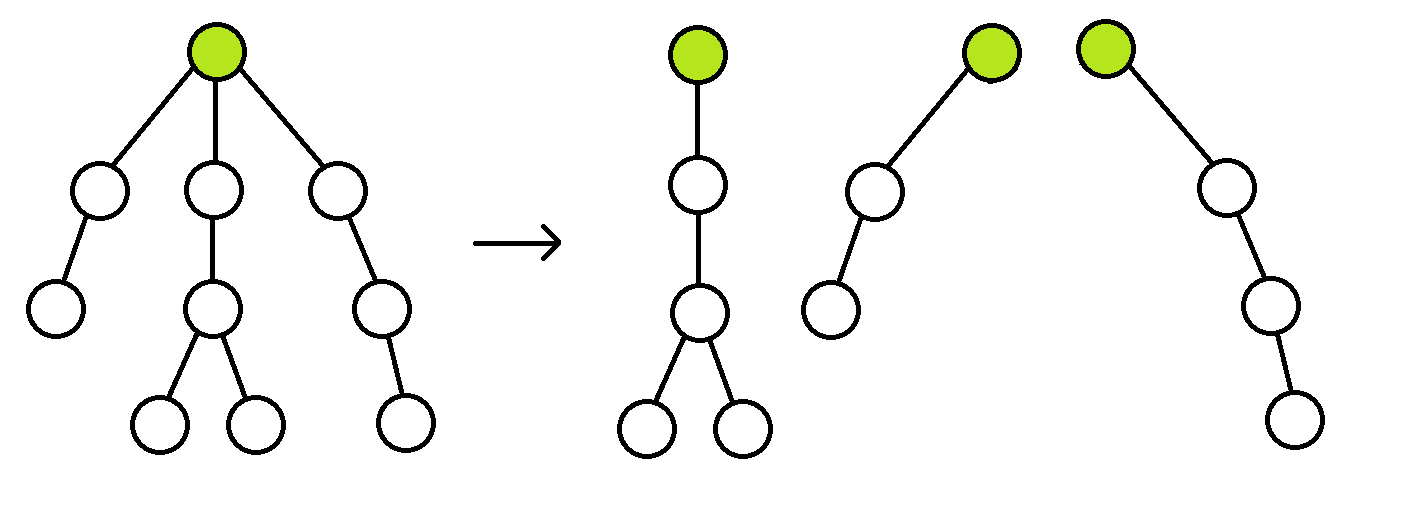
因为不能删根节点，所以这样是可行的。接下来要解决根节点只有一个儿子的情况。

这时候通过观察得到，以根节点的子节点为根的子树，这个点的 \(\text{SG}\) 值加一即为父节点的。

具体证明见 qzhwlzy对博弈论的解读。