3.6 模拟赛T3 题解

题意：

你有一个长度为 \(2\times n+1\) 的随机排列。现在每次操作从排列中间选一个数出来放入一个集合 \(S\) 中（从排列中将其删掉），并且如果不是最后一次操作（即不是序列只剩一个数），我们再在排列中任选一个数并删除它。那么最后 \(S\) 中一定会有 \(n + 1\) 个数，现在我们想知道这个集合中连续值域最长长度是多少。

思路：

首先可以明确一点的是，因为这是排列，所以每一个数都具备唯一性。那么现在我们想要关注最终这个 \(S\) ，有可能变成什么一种形式。重复推一组样例，并且模拟最终不同的 \(S\)。比如：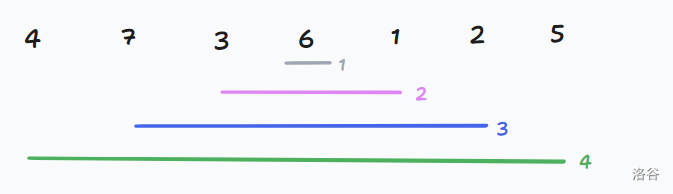

然后你就发现我们第一次只能选数字 \(6\)，然后第二次可以选数字数字 \(1,3\)，第三次按照规律......

分析之后发现只要在当前步数对应的区间中不曾被选择那么就可以选择。然后你还可以发现每个数都会有一个类似于可选机会的信息，比如最中间的我可以有最多次的机会选择，两侧的其次......（受不了了，讲这玩意太抽象了）。

形式化的定义就是：对于每一个数 \(a_i\)，定义 \(pre_{a_i}=\max(2\times n+1-i+1,i)\)。

然后考虑如何判断一段连续值域是否合法，不妨记 \(t_k\) 表示考虑的这一段区间内可选机会小于等于 \(k\) 的元素个数，你发现如果满足：

\[t_k = \sum_{i=l}^r[p_i\leq r] > k
\]

则这个区间无解（这一坨实在是直接用文字描述了，所以请读者结合上述样例理解）。把上述不等式移项得：

\[t_k - k>0
\]

你发现这个玩意看着很舒服，形式整洁，所以定义：

\[f(k)=t_k-k
\]

定义域就是 \([1,n + 1]\)。

如果我们希望这个区间合法，也就等价于希望：

\[\forall_{k\in[1,n+1]}\ f(k)\leq 0
\]

我们如果真的把所有 \(k\) 都这么算出来，复杂度肯定是接受不了的，但是发现上述条件还等价于：

\[\forall_{k\in[1,n+1]}\ f(k)_{\max}\leq0
\]

所以我们只需要维护最大值。这个可以用线段树解决（因为是区间修改加区间查询，树状数组写起来反而更麻烦。）。考虑如何找答案，其实可以双指针，每一次移动指针的判断结合线段树是 \(O(\log n)\)的又因为双指针是 \(O(n)\) 的，所以最后的复杂度是 \(O(n\log n)\)

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
inline int read(){
	char c=getchar();bool f=0;int x=0;
	while(c > '9' || c < '0') f|=c=='-',c=getchar();
	while(c >= '0'&&c <= '9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
	if(f) x=-x;return x;
}
const int N = 4e5 + 10;
struct Segment_tree {
	int lazy,mx;
}t[N << 1];
int n,a[N],pre[N];

void pushup(int rt)
{
	t[rt].mx = std::max(t[rt << 1].mx,t[rt << 1 | 1].mx);
}

void push_down(int rt)
{
	if(t[rt].lazy)
	{
		t[rt << 1].lazy += t[rt].lazy;
		t[rt << 1 | 1].lazy += t[rt].lazy;
		t[rt << 1].mx += t[rt].lazy;
		t[rt << 1 | 1].mx += t[rt].lazy;
		t[rt].lazy = 0;
	}
}

void build(int rt,int l,int r)
{
	t[rt].lazy = 0;
	if(l == r)
	{
		t[rt].mx = -l;
		return ;
	}
	int mid = (l + r) >> 1;
	build(rt << 1,l,mid);
	build(rt << 1 | 1,mid + 1,r);
	pushup(rt);
}

void update(int rt,int l,int r,int L,int R,int x)
{
	if(L <= l && r <= R)
	{
		t[rt].lazy += x;
		t[rt].mx += x;
		return ;
	}
	int mid = (l + r) >> 1;
	push_down(rt);
	if(L <= mid) update(rt << 1,l,mid,L,R,x);
	if(R > mid) update(rt << 1 | 1,mid + 1,r,L,R,x);
	pushup(rt);
}

int main()
{
	n = read();
	for(int i = 1;i <= 2 * n + 1;++i)
	{
		a[i] = read();
		pre[a[i]] = std::min(i,2 * n + 1 - i + 1);
	}

	build(1,1,n + 1);
	int ans = 0;
	int r = 0,l = 1;
	while(l <= 2 * n + 1 && r <= 2 * n + 1)
	{
		while(r <= 2 * n)
		{
			update(1,1,n + 1,pre[++r],n + 1,1);
			if(t[1].mx > 0)
			{
				update(1,1,n + 1,pre[r--],n + 1,-1);
				break;
			}
		}
		ans = std::max(ans,r - l + 1);
		update(1,1,n + 1,pre[l++],n + 1,-1);
	}
	std::cout << ans;
	return 0;
}