HDU 5073 Galaxy（Anshan 2014）（数学推导，贪婪）

Galaxy

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)

Total Submission(s): 556    Accepted Submission(s): 127

Special Judge

Problem Description

Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.






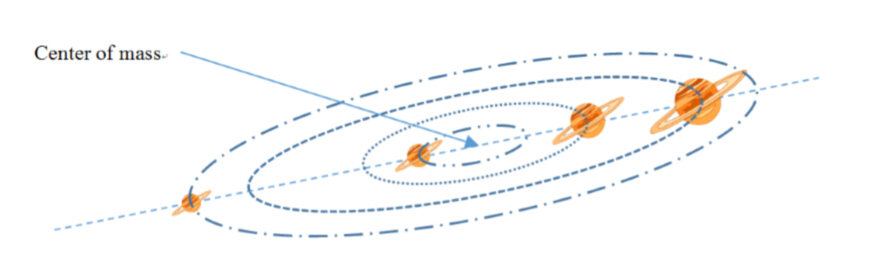
To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.



Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.



The moment of inertia I of a set of n stars can be calculated with the formula






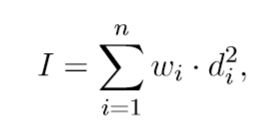
where w_i is the weight of star i, d_i is the distance form star i to the mass of center.



As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial
pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.



Now, you are supposed to calculate the minimum moment of inertia after transportation.

 

Input

The first line contains an integer T (T ≤ 10), denoting the number of the test cases.



For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) and k(0 ≤ k ≤ n), as mentioned above. The next line contains n integers representing the positions of the stars. The absolute values of positions will be no more than 50000.

 

Output

For each test case, output one real number in one line representing the minimum moment of inertia. Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.

 

Sample Input

2
3 2
-1 0 1
4 2
-2 -1 1 2

 

Sample Output

0
0.5

 

Source

field=problem&key=2014+Asia+AnShan+Regional+Contest&source=1&searchmode=source" style="color:rgb(26,92,200); text-decoration:none">2014 Asia AnShan Regional Contest

 

题目大意：数轴上有n个点。每一个点重量1 ，能够移动当中k个点到不论什么位置， 使得题中式子的值最小

解题思路：选择保留区间长度为N - K的连续的数， 然后其余的K个数都移动到这N-K个数的中心。

那个式子事实上表示的是方差。选择的点越密集，方差越小，所以选择连续的N-K个。

其余的假设放到其它地方。肯定没有放到N-K的质心更优。

但这样每次枚举长度为N-K的区间。再计算对应的方差。复杂度为O（NK），会超时。所以通过数学推导变形，避免反复计算。详细例如以下：

第i个到第i+n-k-1个的

方差 = (Xi - X)^2 + (Xi+1 - X)^2 + ... + (Xi+n-k-1 - X)^2                              （当中X表示Xi,Xi+1, ... , Xi+n-k-1的平均值）

= Xi^2 + Xi+1^2 + ... + Xi+n-k-1^2 - 2X(Xi + Xi+1 + ... Xi+n-k-1)        （令sum2=Xi^2 + Xi+1^2 + ... + Xi+n-k-1^2，sum1=Xi+Xi+1+ ... +Xi+n-k-1）

= sum2 - sum1^2 / (n - k)

所以，排序后维护两种前缀，O（n）扫描。取方差的最小值就可以。

參考代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;

const int MAXN = 50010;
const double INF = 1e20;
int n, k, nCase;
double p[MAXN], sum1[MAXN], sum2[MAXN], ans;

void init() {
    ans = INF;
    sum1[0] = sum2[0] = 0.0;
}

void input() {
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i++) {
        scanf("%lf", &p[i]);
    }
}

void solve() {
    if (n == k) {
        printf("%.10lf\n", 0);
        return;
    }
    sort(p+1, p+n+1);
    for (int i = 1; i <= n; i++) {
        sum1[i] = sum1[i-1] + p[i];
        sum2[i] = sum2[i-1] + p[i]*p[i];
    }
    for (int i = 1; i <= k+1; i++) {
        double s1 = sum1[i+n-k-1] - sum1[i-1];
        double s2 = sum2[i+n-k-1] - sum2[i-1];
        double tmp = s2 - s1*s1 / (n-k);
        if (tmp < ans) ans = tmp;
    }

    printf("%.10lf\n", ans);
}

int main() {
    scanf("%d", &nCase);
    while (nCase--) {
        init();
        input();
        solve();
    }
    return 0;
}

版权声明：本文博客原创文章，博客，未经同意，不得转载。