LeetCode Golang 4. 寻找两个有序数组的中位数

4. 寻找两个有序数组的中位数

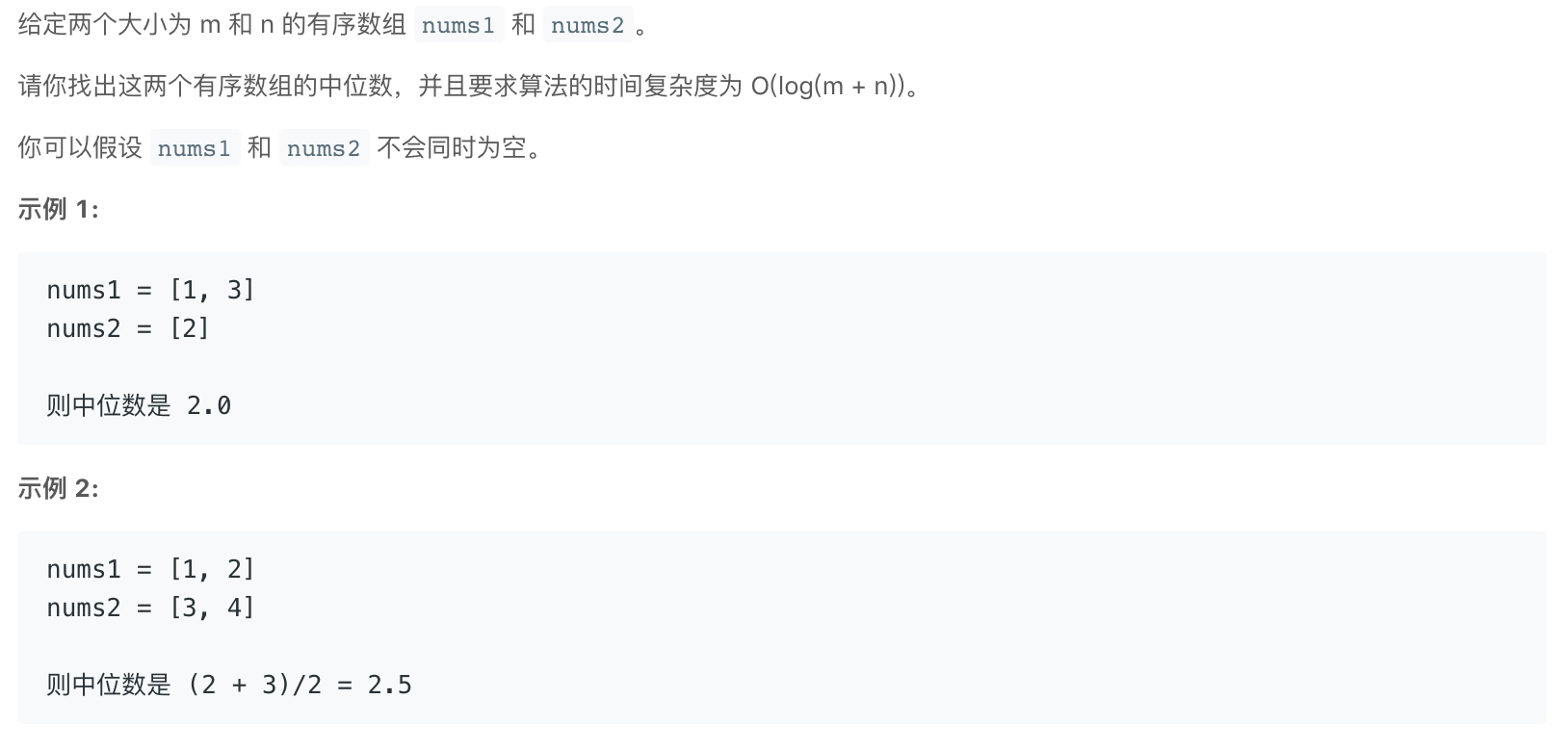
很明显我偷了懒， 没有给出正确的算法，因为官方的解法需要时间仔细看一下。。。

func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {

	// 追加 -> 排序 -> 求中值
	nums1 = append(nums1, nums2...)
	if len(nums1) == 0 {
		return 0.0
	}
	// 排序
	sort.Ints(nums1)
	//fmt.Println(nums1)

	// 求中值,偶数个求中间均值， 奇数个取中间
	if len(nums1)%2 == 0{
		return float64(nums1[len(nums1)/2]+nums1[len(nums1)/2-1])/2
	} else {
		return float64(nums1[len(nums1)/2])
	}

}

　　

这里有 LeetCode 上大神给出的符合要求的解答：

执行时间 28ms， 大神解答：

// O(log(m + n))算法，假设第k个元素是中位数，则在nums1和nums2的混合集合中找到第k个元素
// 在nums1和nums2中各拿出k/2个元素，比较各自中最大的一个，这样每比较一次就会找到k/2个比k小的元素
// 此时在剩下的集合中查找第k/2个元素，以此类推，当k为0时就找到了中位数（但是k不会为0，只会是1，所以当k为1时比较两个序列中首元素小的那个）
// 当某个序列中所有元素都比第k个元素小时，就返回另一个队列中的第k个元素
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
	len := len(nums2) + len(nums1)
	k := len / 2
	if len % 2 == 0 {
		return (helper(nums1, 0, nums2, 0, k + 1) + helper(nums1, 0, nums2, 0, k)) / 2.0
	} else {
		return helper(nums1, 0, nums2, 0, k + 1)
	}
}

/*
* 依据上面的算法查找中位数
* n,m分别记录nums1和nums2在哪个位置之前的数据已被筛选
*/
func helper(nums1 []int, n int, nums2 []int, m int, k int) float64{
	if n >= len(nums1){
		return float64(nums2[m + k - 1])
	} else if m >= len(nums2) {
		return float64(nums1[n + k - 1])
	}
	if k == 1{
		a := math.Min(float64(nums1[n]), float64(nums2[m]))
		return a
	}

	p1 := n + k/2 - 1
	p2 := m + k - k/2 - 1
	var mid1, mid2 int
	if p1 >= len(nums1) {
		mid2 = nums2[p2]
		mid1 = mid2 + 1
	} else if p2 >= len(nums2) {
		mid1 = nums1[p1]
		mid2 = mid1 + 1
	} else {
		mid1 = nums1[p1]
		mid2 = nums2[p2]
	}

	if mid1 < mid2 {
		k = k - (p1 + 1 - n)
		if k == 0{
			return float64(mid2)
		}
		return helper(nums1, p1+1, nums2, m, k)
	} else {
		k = k - (p2 + 1 - m)
		if k == 0{
			return float64(mid1)
		}
		return helper(nums1, n, nums2, p2+1, k)
	}
}

　　 LeetCode 深似海。。。