还记得高中的向量吗？leetcode 335. Self Crossing（判断线段相交）

传统解法

题目来自 leetcode 335. Self Crossing。

题意非常简单，有一个点，一开始位于 (0, 0) 位置，然后有规律地往上，左，下，右方向移动一定的距离，判断是否会相交（self crossing）。

一个很容易想到的方案就是求出所有线段，然后用 O(n^2) 的时间复杂度两两判断线段是否相交，而线段相交的判断，可以列个二元一次方程求解（交点）。这个解法非常容易想到，但是实际操作起来比较复杂，接下去介绍利用向量的解法。

向量解法

简单回顾下向量，具体的自行谷歌。向量就是一条有向线段，这里要用到的是向量的 叉乘。（还有个类似的概念叫做 点积）

叉乘公式：

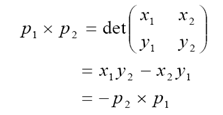
而因为 p1 X p2 = | a | * | b | * sin α，后者又是平行四边形的面积公式，所以可以用叉乘来求解平行四边形的面积（同理可以求解三角形的面积）。PS：如果给出三个点坐标，求解三角形面积的话，最好用叉乘来做，这样更精确，而不是海伦公式。

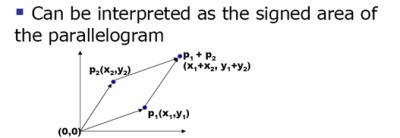
向量叉乘还能判断 p0p1 和 p0p2 两个向量， 对于 p0 点而言，p0p1 是位于 p0p2 顺时针方向，还是逆时针方向。

我们回到判断线段相交，两线段相交有如下两种可能。

对于第一种情况，我们可以判断 p1, p2 两点分别位于线段 p3p4 两边，同时满足 p3, p4 两点分别位于线段 p1p2 两边。如何判断？以判断 p1，p2 是否位于线段 p3p4 两边为例，求解叉乘 p3p1 X p3p4，以及 p3p2 X p3p4，如果符合条件，两值必是一正一负。对于第二种情况，因为共线，所以叉乘结果为 0，但是叉乘结果为 0 只能保证共线，并不能保证相交，所以还需要进行如下的判断。

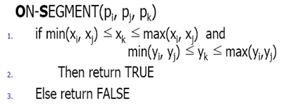
这样解法就呼之欲出了，贡献个判断线段相交的模板：

/**
 * @param {object} a
 * @param {object} b
 * @return {boolean}
 * a, b 表示两条线段。
 * (a.x1, a.y1), (a.x2, a.y2) 分别表示线段 a 两个端点; b 类似
 */

function f(a, b) {

  function online(a, b, c) {
    if (a.x >= Math.min(b.x, c.x) && a.x <= Math.max(b.x, c.x) && a.y >= Math.min(b.y, c.y) && a.y <= Math.max(b.y, c.y))
      return true;

    return false;
  }

  var n1, n2, n3, n4;

  n1 = (a.x1 - b.x2) * (b.y1 - b.y2) - (a.y1 - b.y2) * (b.x1 - b.x2);
  n2 = (a.x2 - b.x2) * (b.y1 - b.y2) - (a.y2 - b.y2) * (b.x1 - b.x2);
  n3 = (b.x1 - a.x2) * (a.y1 - a.y2) - (b.y1 - a.y2) * (a.x1 - a.x2);
  n4 = (b.x2 - a.x2) * (a.y1 - a.y2) - (b.y2 - a.y2) * (a.x1 - a.x2);

  if (n1 * n2 < 0 && n3 * n4 < 0)
    return 1;

  var p1 = {x: a.x1, y: a.y1};

  var p2 = {x: a.x2, y: a.y2};

  var p3 = {x: b.x1, y: b.y1};

  var p4 = {x: b.x2, y: b.y2};

  if (n1 === 0 && online(p1, p3, p4))
    return 1;

  if (n2 === 0 && online(p2, p3, p4))
    return 1;

  if (n3 === 0 && online(p3, p1, p2))
    return 1;

  if (n4 === 0 && online(p4, p1, p2))
    return 1;

  return 0;
}

本题完整代码详见 https://github.com/hanzichi/leetcode/tree/master/Algorithms/Self%20Crossing，求 star， 求 fork，求 follow