CF #305 (Div. 2) C. Mike and Frog(扩展欧几里得&&当然暴力is also no problem）

C. Mike and Frog

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mike has a frog and a flower. His frog is named Xaniar and his flower is named Abol. Initially(at time 0), height of Xaniar is h₁ and height of Abol is h₂. Each second, Mike waters Abol and Xaniar.

So, if height of Xaniar is h₁ and height of Abol is h₂, after one second height of Xaniar will become  and height of Abol will become  where x₁, y₁, x₂ and y₂ are some integer numbers and  denotes the remainder of amodulo b.

Mike is a competitive programmer fan. He wants to know the minimum time it takes until height of Xania is a₁ and height of Abol is a₂.

Mike has asked you for your help. Calculate the minimum time or say it will never happen.

Input

The first line of input contains integer m (2 ≤ m ≤ 10⁶).

The second line of input contains integers h₁ and a₁ (0 ≤ h₁, a₁ < m).

The third line of input contains integers x₁ and y₁ (0 ≤ x₁, y₁ < m).

The fourth line of input contains integers h₂ and a₂ (0 ≤ h₂, a₂ < m).

The fifth line of input contains integers x₂ and y₂ (0 ≤ x₂, y₂ < m).

It is guaranteed that h₁ ≠ a₁ and h₂ ≠ a₂.

Output

Print the minimum number of seconds until Xaniar reaches height a₁ and Abol reaches height a₂ or print -1 otherwise.

Sample test(s)

input

5 
4 2 
1 1 
0 1 
2 3

output

3

input

1023 
1 2 
1 0 
1 2 
1 1

output

-1

题解：

In this editorial, consider p = m, a = h₁, a′ = a₁, b = h₂ and b′ = a₂.

First of all, find the number of seconds it takes until height of Xaniar becomes a′ (starting from a) and call it q. Please note that q ≤ pand if we don't reach a′ after p seconds, then answer is  - 1.

If after q seconds also height of Abol will become equal to b′ then answer if q.

Otherwise, find the height of Abdol after q seconds and call it e.

Then find the number of seconds it takes until height of Xaniar becomes a′ (starting from a′) and call it c. Please note that c ≤ p and if we don't reach a′ after p seconds, then answer is  - 1.

if g(x) = Xx + Y, then find f(x) = g(g(...(g(x)))) (c times). It is really easy:

c = 1, d = 0
for i = 1 to c
     c = (cX) % p
     d = (dX + Y) % p

Then,

f(x)
     return (cx + d) % p

Actually, if height of Abol is x then, after c seconds it will be f(x).

Then, starting from e, find the minimum number of steps of performing e = f(e) it takes to reach b′ and call it o. Please note thato ≤ p and if we don't reach b′ after p seconds, then answer is  - 1.

Then answer is x + c × o.

Time Complexity: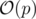 

 #include<stdio.h>
 #include<string.h>
 #include<algorithm>
 typedef long long ll ;
 ll mod ;
 ll a , a1 ;
 ll x , y ;
 ll b , b1 ;
 ll _x , _y ;
 ll A , T ;
 ll B , _T ;

 ll exgcd (ll a,ll b,ll& x,ll &y)
  {
      if(b==){
          x=;
          y=;
          return a;
      }
     ll d = exgcd ( b , a % b , x , y ) ;
     ll tmp = x ;
     x = y ;
     y = tmp - a / b * y ;
     return d;
 }
 //用扩展欧几里得算法解线性方程ax+by=c;
 void __exgcd(ll a , ll b , ll c )
 {
     ll x , y ;
     ll d = exgcd ( a , b , x , y ) ;
     if(c % d) {
         puts ("-1") ;
         return ;
     }

     ll k = c / d ;
     x *= k ; y *= k ;//求的只是其中一个解
     if (d < ) d = -d ;
     ll t1 = T / d , t2 = _T / d ;
    // printf ("t1 = %I64d , t2 = %I64d\n" , t1 , t2 ) ;
     //printf ("x = %I64d , y = %I64d\n" , x , y ) ;
     if (x <  || y < ) {
         while (x <  || y < ) {
             x += t1 ;
             y += t2 ;
         }
     }
     else {
         while (x >=  && y >= ) {
             x -= t1 ;
             y -= t2 ;
         }
         x += t1 ;
         y += t2 ;
     }
     //printf ("x = %I64d , y = %I64d\n" , x , y ) ;
     printf ("%I64d\n" , A + T * y) ;
 }

 bool workA ()
 {
     ll cnt =  ;
     ll c = a  ;
     while () {
         cnt ++ ;
         c = (c * x + y) % mod ;
         if (c == a1) {
             A = cnt ;
             return true ;
         }
         if (cnt > mod) break ;
     }
     return false ;
 }

 bool workB ()
 {
     ll cnt =  ;
     ll c = b  ;
     while () {
         cnt ++ ;
         c = (c * _x + _y) % mod ;
         if (c == b1) {
             B = cnt ;
             return true ;
         }
         if (cnt > mod) break ;
     }
     return false ;
 }

 bool workT ()
 {
     T =  ;
     ll cnt =  ;
     ll c = a1  ;
     while () {
         cnt ++ ;
         c = (c * x + y) % mod ;
         if (c == a1) {
             T = cnt ;
             return true ;
         }
         if (cnt > mod) break ;
     }
     return false ;
 }

 bool work_T ()
 {
     _T =  ;
     ll cnt =  ;
     ll c = b1  ;
     while () {
         cnt ++ ;
         c = (c * _x + _y) % mod ;
         if (c == b1) {
             _T = cnt ;
             return true ;
         }
         if (cnt > mod) break ;
     }
     return false ;
 }

 int main ()
 {
     //freopen ("a.txt" , "r" , stdin ) ;
     while (~ scanf ("%I64d" , &mod)) {
         scanf ("%I64d%I64d%I64d%I64d" , &a , &a1 , &x , &y) ;
         scanf ("%I64d%I64d%I64d%I64d" , &b , &b1 , &_x , &_y) ;
         if (!workA ())  puts ("-1") ;
         else {
             if (!workB ()) puts ("-1") ;
             else if (A == B) printf ("%I64d\n" , A) ;
             else {
                 workT () ;
                 work_T () ;
                 if (T ==  || _T == ) {
                     if (T ==  && _T == ) puts ("-1") ;
                     else if (T ==  ) {
                         if (A - B >=  && (A - B) % _T == ) printf ("%I64d\n" , A) ;
                         else puts ("-1") ;
                     }
                     else if (_T == ) {
                         if (B - A >=  && (B - A) % T == ) printf ("%I64d\n" , B) ;
                         else puts ("-1") ;
                     }
                 } else {
                     ll a = _T , b = -T , c = A - B ;
                     __exgcd (a , b , c) ;
                 }
             }
         }
     }
     return  ;
 }

题解：

一般情况：我们能用暴力求出a-->a1所需时间A ， b-->b1所需时间B，a1-->a1时间Ta ， b1-->b1时间Tb；

注意：A , B , Ta , Tb 都会在 “mod 时间”内完成，若没在这段时间内找到，则不存在。

所以为了达到目标显然需要满足一下等式：A + x * Ta = B + y * Tb ---- ①---> A - B = - Ta * x + Tb * y ----②;

那么问题就转变成了求该方程是否有整数解(这道题有整数解，就必有正整数解）。

根据扩展欧几里得算法：

　　　　　　c = a * x + b * y ;

只要满足gcd (a , b) | c （及a,b的gcd为c的约数）时，该方程必有解，我们令 d = gcd (a , b) ;

则存在解时：(下面的_x , _y都假定为执行完 exgcd（a , b , x , y）后产生的 _x , _y)

其中一组特解：x' = _x * c / d ;(c = A - B)

　　　　　　　y' = _y * c / d ;

递推式：

　　　　x = x' + Ta / fabs (d)  * k ;( k 为 参数）

　　　　y = y' + Tb / fabs (d)  * k ；

然后我们只要暴力求出可行解(x , y)中与0最接近的即可 ， A + x * Ta 及为答案。

暴力枚举：(简洁，大神的）

 #include <cstring>
 #include <map>
 #include <deque>
 #include <queue>
 #include <stack>
 #include <sstream>
 #include <iostream>
 #include <cstdio>
 #include <cmath>
 #include <math.h>
 #include <ctime>
 #include <algorithm>
 #include <vector>
 #include <set>
 #include <list>
 #include <climits>
 #include <cctype>
 #include <bitset>
 #include <iostream>
 #include <complex>

 using namespace std;

 typedef stringstream ss;
 typedef long long ll;
 typedef pair<ll, ll> ii;
 typedef vector<vector<ii> > vii;
 typedef vector<string> vs;
 typedef vector<ll> vi;
 typedef vector<double> vd;
 typedef long double ld;
 typedef vector<vector<ll> > matrix;
 typedef complex<double> point;

 #define all(v) v.begin(), v.end()
 #define rall(v) v.rbegin(), v.rend()
 #define sz(v) ((ll)v.size())
 #define clr(v, d) memset(v, d, sizeof(v))
 #define polar(r,t) ((r)*exp(point(0,(t))))
 #define length(a) hypot((a).real(),(a).imag())
 #define angle(a) atan2((a).imag() , (a).real())
 #define vec(a,b) ((b)-(a))
 #define dot(a,b) ((conj(a)*(b)).real())
 #define cross(a,b) ((conj(a)*(b)).imag())
 #define lengthSqr(a) dot(a,a)
 #define rotate(v,t) ((v)*exp(point(0,t)))
 #define rotateAbout(v,t,a) (rotate(vec(a,v),t)+(a))
 #define reflect(v,m) (conj((v)/(m))*m)
 #define dist(a,b) (sqrt(pow((a).real()-(b).real(),2.0)+pow((a).imag()-(b).imag(),2.0)))
 #define normalize(a) ((a)/length(a))

 int dx[] = { , -, ,  };
 int dy[] = { , , , - };
 double PI = 3.1415926535897932384626433832795;

 const ll oo = (ll) 1e9 + ;
 const double eps = 1e-;
 const ll mod = ;

 int main() {
     //freopen("a.txt", "r", stdin);
     ios_base::sync_with_stdio();
     ll m, h1, a1, x1, y1, h2, a2, x2, y2;
     cin >> m >> h1 >> a1 >> x1 >> y1 >> h2 >> a2 >> x2 >> y2;
     ll idx1 = -, idx2 = -;
     for (int i = ; i <= m; i++) {
         h1 = (x1 * h1 + y1) % m;
         if (h1 == a1) {
             idx1 = i;
             break;
         }
     }
     for (int i = ; i <= m; i++) {
         h2 = (x2 * h2 + y2) % m;
         if (h2 == a2) {
             idx2 = i;
             break;
         }
     }

     if (idx1 == - || idx2 == -) {
         cout << "-1" << endl;
         return ;
     }

     ll step1, step2;
     for (int i = ; i <= m; i++) {
         h1 = (x1 * h1 + y1) % m;
         if (h1 == a1) {
             step1 = i;
             break;
         }
     }
     for (int i = ; i <= m; i++) {
         h2 = (x2 * h2 + y2) % m;
         if (h2 == a2) {
             step2 = i;
             break;
         }
     }
     //printf ("idx1 = %I64d , idx2 = %I64d , step1 = %I64d, step2 = %I64d\n" , idx1 , idx2 , step1 , step2 ) ;
     for (int i = ; i <=  * m; i++) {
         if (idx1 == idx2) {
             cout << idx1 << endl;
             return ;
         }
         if (idx1 > idx2) {
             idx2 += step2;
         } else {
             idx1 += step1;
         }
     }
     cout << "-1" << endl;
     return ;
 }