CF149D. Coloring Brackets[区间DP !]

题意：给括号匹配涂色，红色蓝色或不涂，要求见原题，求方案数

---

区间DP

用栈先处理匹配

f[i][j][0/1/2][0/1/2]表示i到ji涂色和j涂色的方案数

l和r匹配的话，转移到(l+1,r-1)

不匹配，i的匹配p一定在l和r之间，从p分开转移

听说用记忆化搜索比较快，可以像树形DP那样写记忆化搜索，也可以传统的四个参数那样写

用循环+条件判断，简化状态转移的枚举

注意细节 见代码

---

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=,MOD=1e9+;
char s[N];
long long n,f[N][N][][];
int st[N],top=,m[N];
void match(){
    for(int i=;i<=n;i++){
        if(s[i]=='(') st[++top]=i;
        else{
            int tmp=st[top--];
            m[i]=tmp;
            m[tmp]=i;
        }
    }
}
void dp(int l,int r){//printf("dp %d %d\n",l,r);
    if(l>=r) return;
    if(l+==r){
        f[l][r][][]=f[l][r][][]=f[l][r][][]=f[l][r][][]=;
        return;
    }
    if(m[l]==r){
        dp(l+,r-);
        for(int i=;i<;i++)
            for(int j=;j<;j++){
                if(j!=) f[l][r][][]=(f[l][r][][]+f[l+][r-][i][j])%MOD;
                if(j!=) f[l][r][][]=(f[l][r][][]+f[l+][r-][i][j])%MOD;
                if(i!=) f[l][r][][]=(f[l][r][][]+f[l+][r-][i][j])%MOD;
                if(i!=) f[l][r][][]=(f[l][r][][]+f[l+][r-][i][j])%MOD;
            }
    }else{
        int p=m[l];
        dp(l,p);dp(p+,r);
        for(int i=;i<;i++)
            for(int j=;j<;j++)
                for(int k=;k<;k++)
                    for(int t=;t<;t++){
                        if(k==&&t==) continue;
                        if(k==&&t==) continue;
                        //if(i!=0&&t!=0) continue; 不需要，因为已保证这样的话值是0
                        f[l][r][i][j]=(f[l][r][i][j]+f[l][p][i][k]*f[p+][r][t][j]%MOD)%MOD;
                    }
    }
    //printf("%d %d  %d %d %d %d\n",l,r,f[l][r][0][1],f[l][r][0][2],f[l][r][1][0],f[l][r][2][0]);
}
//void dp(int l,int r,int a,int b){
//    int &ans=f[l][r][a][b];
//    if(ans!=-1) return ans;
//
//}
int main(){
    scanf("%s",s+);
    n=strlen(s+);
    match();
    dp(,n);
    long long ans=;
    for(int i=;i<;i++)
        for(int j=;j<;j++)
            ans=(ans+f[][n][i][j])%MOD;

    printf("%d",ans);
}

D. Coloring Brackets

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Once Petya read a problem about a bracket sequence. He gave it much thought but didn't find a solution. Today you will face it.

You are given string s. It represents a correct bracket sequence. A correct bracket sequence is the sequence of opening ("(") and closing (")") brackets, such that it is possible to obtain a correct mathematical expression from it, inserting numbers and operators between the brackets. For example, such sequences as "(())()" and "()" are correct bracket sequences and such sequences as ")()" and "(()" are not.

In a correct bracket sequence each bracket corresponds to the matching bracket (an opening bracket corresponds to the matching closing bracket and vice versa). For example, in a bracket sequence shown of the figure below, the third bracket corresponds to the matching sixth one and the fifth bracket corresponds to the fourth one.

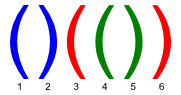
You are allowed to color some brackets in the bracket sequence so as all three conditions are fulfilled:

• Each bracket is either not colored any color, or is colored red, or is colored blue.
• For any pair of matching brackets exactly one of them is colored. In other words, for any bracket the following is true: either it or the matching bracket that corresponds to it is colored.
• No two neighboring colored brackets have the same color.

Find the number of different ways to color the bracket sequence. The ways should meet the above-given conditions. Two ways of coloring are considered different if they differ in the color of at least one bracket. As the result can be quite large, print it modulo1000000007 (109 + 7).

Input

The first line contains the single string s (2 ≤ |s| ≤ 700) which represents a correct bracket sequence.

Output

Print the only number — the number of ways to color the bracket sequence that meet the above given conditions modulo 1000000007(109 + 7).

Examples

input

(())

output

12

input

(()())

output

40

input

()

output

4

Note

Let's consider the first sample test. The bracket sequence from the sample can be colored, for example, as is shown on two figures below.

The two ways of coloring shown below are incorrect.

---