BZOJ3839 : [Pa2013]Działka

对于每个询问，首先可以通过扫描线+线段树求出四个方向的第一个点，询问范围等价于框住这些点的最小矩形。

对于一个点$i$，预处理出：

$A[i][j]$：$i$往左下角按凸壳走到$j$时，凸壳上相邻两点的叉积和。

$B[i][j]$：$i$往右下角按凸壳走到$j$时，凸壳上相邻两点的叉积和。

$C[i][j]$：$i$往左上角按凸壳走到$j$时，凸壳上相邻两点的叉积和。

$D[i][j]$：$i$往右上角按凸壳走到$j$时，凸壳上相邻两点的叉积和。

注意到每个数组只有一半有用，所以可以把$AD$合并、$BC$合并。

那么答案相当于在$4$个边界点上按凸包走一圈的叉积和再除以二，如下图，这可以$O(1)$计算。

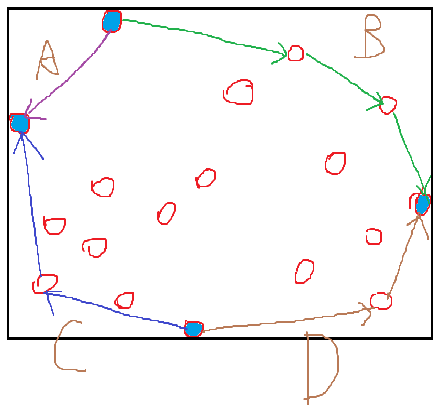
时间复杂度$O(n^2+m\log m)$。

#include<cstdio>
#include<algorithm>
using std::sort;
typedef long long ll;
const int N=3005,M=1000010;
int K,n,m,i,j,k,t,q[N];ll A[N][N],B[N][N],ans;
struct P{
  int x,y,p;
  inline ll operator*(const P&b){return 1LL*x*b.y-1LL*y*b.x;}
}a[N];
inline bool cmpA(const P&a,const P&b){return a.x==b.x?a.y<b.y:a.x<b.x;}
inline bool cmpB(const P&a,const P&b){return a.x==b.x?a.y>b.y:a.x<b.x;}
inline bool cmpx(const P&a,const P&b){return a.x<b.x;}
inline bool cmpy(const P&a,const P&b){return a.y<b.y;}
struct Q{
  int a,b,c,d;
  Q(){}
  Q(int _a,int _b,int _c,int _d){a=_a,b=_b,c=_c,d=_d;}
}que[M],e[M];
int NA[M],NB[M],NC[M],ND[M];
inline bool cmpE(const Q&a,const Q&b){return a.a<b.a;}
int T[2100000],vis[N],pos;
void build(int x,int a,int b){
  T[x]=0;
  if(a==b)return;
  int mid=(a+b)>>1;
  build(x<<1,a,mid),build(x<<1|1,mid+1,b);
}
void change(int x,int a,int b,int c,int p){
  T[x]=p;
  if(a==b)return;
  int mid=(a+b)>>1;
  if(c<=mid)change(x<<1,a,mid,c,p);else change(x<<1|1,mid+1,b,c,p);
}
inline int merge(int x,int y){return vis[x]>vis[y]?x:y;}
int ask(int x,int a,int b,int c,int d){
  if(c<=a&&b<=d)return T[x];
  int mid=(a+b)>>1,t=0;
  if(c<=mid)t=ask(x<<1,a,mid,c,d);
  if(d>mid)t=merge(t,ask(x<<1|1,mid+1,b,c,d));
  return t;
}
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
int main(){
  read(K),read(n);
  for(i=1;i<=n;i++)read(a[i].x),read(a[i].y),a[i].p=i;
  sort(a+1,a+n+1,cmpA);
  for(i=2;i<=n;i++){
    k=a[q[t=0]=i].p;
    for(j=i-1;j;j--)if(a[j].y<=a[i].y){
      while(t&&1LL*(a[q[t-1]].x-a[q[t]].x)*(a[q[t]].y-a[j].y)<1LL*(a[q[t]].x-a[j].x)*(a[q[t-1]].y-a[q[t]].y))t--;
      A[k][a[j].p]=A[k][a[q[t]].p]+a[q[t]]*a[j];
      q[++t]=j;
    }
  }
  for(i=1;i<n;i++){
    k=a[q[t=0]=i].p;
    for(j=i+1;j<=n;j++)if(a[j].y>=a[i].y){
      while(t&&1LL*(a[q[t]].x-a[q[t-1]].x)*(a[j].y-a[q[t]].y)<1LL*(a[j].x-a[q[t]].x)*(a[q[t]].y-a[q[t-1]].y))t--;
      A[k][a[j].p]=A[k][a[q[t]].p]+a[q[t]]*a[j];
      q[++t]=j;
    }
  }
  sort(a+1,a+n+1,cmpB);
  for(i=1;i<n;i++){
    k=a[q[t=0]=i].p;
    for(j=i+1;j<=n;j++)if(a[j].y<=a[i].y){
      while(t&&1LL*(a[q[t]].x-a[q[t-1]].x)*(a[j].y-a[q[t]].y)>1LL*(a[j].x-a[q[t]].x)*(a[q[t]].y-a[q[t-1]].y))t--;
      B[k][a[j].p]=B[k][a[q[t]].p]+a[q[t]]*a[j];
      q[++t]=j;
    }
  }
  for(i=2;i<=n;i++){
    k=a[q[t=0]=i].p;
    for(j=i-1;j;j--)if(a[j].y>=a[i].y){
      while(t&&1LL*(a[q[t-1]].x-a[q[t]].x)*(a[q[t]].y-a[j].y)>1LL*(a[q[t]].x-a[j].x)*(a[q[t-1]].y-a[q[t]].y))t--;
      B[k][a[j].p]=B[k][a[q[t]].p]+a[q[t]]*a[j];
      q[++t]=j;
    }
  }
  read(m);
  for(i=1;i<=m;i++)read(que[i].a),read(que[i].b),read(que[i].c),read(que[i].d);
  for(i=1;i<=m;i++)e[i]=Q(que[i].d,que[i].a,que[i].b,i);
  sort(a+1,a+n+1,cmpy),sort(e+1,e+m+1,cmpE);
  for(build(1,0,K),i=j=1;i<=m;i++){
    while(j<=n&&a[j].y<=e[i].a)change(1,0,K,a[j].x,a[j].p),vis[a[j].p]=++pos,j++;
    NA[e[i].d]=ask(1,0,K,e[i].b,e[i].c);
  }
  for(i=1;i<=m;i++)e[i]=Q(que[i].c,que[i].a,que[i].b,i);
  sort(a+1,a+n+1,cmpy),sort(e+1,e+m+1,cmpE);
  for(build(1,0,K),i=m,j=n;i;i--){
    while(j&&a[j].y>=e[i].a)change(1,0,K,a[j].x,a[j].p),vis[a[j].p]=++pos,j--;
    NC[e[i].d]=ask(1,0,K,e[i].b,e[i].c);
  }
  for(i=1;i<=m;i++)e[i]=Q(que[i].b,que[i].c,que[i].d,i);
  sort(a+1,a+n+1,cmpx),sort(e+1,e+m+1,cmpE);
  for(build(1,0,K),i=j=1;i<=m;i++){
    while(j<=n&&a[j].x<=e[i].a)change(1,0,K,a[j].y,a[j].p),vis[a[j].p]=++pos,j++;
    ND[e[i].d]=ask(1,0,K,e[i].b,e[i].c);
  }
  for(i=1;i<=m;i++)e[i]=Q(que[i].a,que[i].c,que[i].d,i);
  sort(a+1,a+n+1,cmpx),sort(e+1,e+m+1,cmpE);
  for(build(1,0,K),i=m,j=n;i;i--){
    while(j&&a[j].x>=e[i].a)change(1,0,K,a[j].y,a[j].p),vis[a[j].p]=++pos,j--;
    NB[e[i].d]=ask(1,0,K,e[i].b,e[i].c);
  }
  for(i=1;i<=m;i++){
    ans=A[NA[i]][NB[i]]-B[NA[i]][ND[i]]-B[NC[i]][NB[i]]+A[NC[i]][ND[i]];
    printf("%lld.%d\n",ans>>1LL,ans&1LL?5:0);
  }
  return 0;
}