LIS 最长递增子序列

一、最长公共子序列

　　经典的动态规划问题，大概的陈述如下：

　　给定两个序列a1,a2,a3,a4,a5,a6......和b1,b2,b3,b4,b5,b6.......,要求这样的序列使得c同时是这两个序列中的部分（不要求连续），这个就叫做公共子序列，然后最长公共子序列自然就是所有的子序列中最长的啦。

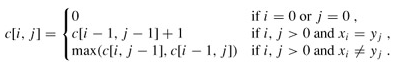
    public static int lcs(String s1, String s2) {
        int[][] dp = new int[s1.length()+1][s2.length()+1];
        for (int i=1; i<=s1.length(); i++) {
            for (int j=1; j<=s2.length(); j++) {
                if (s1.charAt(i-1) == s2.charAt(j-1)) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return dp[s1.length()][s2.length()];
    }

二、最长递增子序列

最长递增子序列，Longest Increasing Subsequence 下面我们简记为 LIS。

方法一、排序+LCS

转化成LCS问题求解，只要将这个序列排序之后与原来的序列求LCS得到的就是LIS了。

方法二、DP

像LCS一样，从后向前分析，很容易想到，第i个元素之前的最长递增子序列的长度要么是1（单独成一个序列），要么就是第i-1个元素之前的最长递增子序列加1，可以有状态方程：

LIS[i] = max{1,LIS[k]+1}，其中，对于任意的k<=i-1，arr[i] > arr[k]，这样arr[i]才能在arr[k]的基础上构成一个新的递增子序列。

方法三、

假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7，可以看出来它的LIS长度为5。
下面一步一步试着找出它。
我们定义一个序列B，然后令 i = 1 to 9 逐个考察这个序列。
此外，我们用一个变量Len来记录现在最长算到多少了

首先，把d[1]有序地放到B里，令B[1] = 2，就是说当只有1一个数字2的时候，长度为1的LIS的最小末尾是2。这时Len=1

然后，把d[2]有序地放到B里，令B[1] = 1，就是说长度为1的LIS的最小末尾是1，d[1]=2已经没用了，很容易理解吧。这时Len=1

接着，d[3] = 5，d[3]>B[1]，所以令B[1+1]=B[2]=d[3]=5，就是说长度为2的LIS的最小末尾是5，很容易理解吧。这时候B[1..2] = 1, 5，Len＝2

再来，d[4] = 3，它正好加在1,5之间，放在1的位置显然不合适，因为1小于3，长度为1的LIS最小末尾应该是1，这样很容易推知，长度为2的LIS最小末尾是3，于是可以把5淘汰掉，这时候B[1..2] = 1, 3，Len = 2

继续，d[5] = 6，它在3后面，因为B[2] = 3, 而6在3后面，于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6，还是很容易理解吧？ Len = 3 了噢。

第6个, d[6] = 4，你看它在3和6之间，于是我们就可以把6替换掉，得到B[3] = 4。B[1..3] = 1, 3, 4， Len继续等于3

第7个, d[7] = 8，它很大，比4大，嗯。于是B[4] = 8。Len变成4了

第8个, d[8] = 9，得到B[5] = 9，嗯。Len继续增大，到5了。

最后一个, d[9] = 7，它在B[3] = 4和B[4] = 8之间，所以我们知道，最新的B[4] =7，B[1..5] = 1, 3, 4, 7, 9，Len = 5。

于是我们知道了LIS的长度为5。

!!!!! 注意。这个1,3,4,7,9不是LIS，它只是存储的对应长度LIS的最小末尾。有了这个末尾，我们就可以一个一个地插入数据。虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义，但是如果后面再出现两个数字 8 和 9，那么就可以把8更新到d[5], 9更新到d[6]，得出LIS的长度为6。

然后应该发现一件事情了：在B中插入数据是有序的，而且是进行替换而不需要挪动——也就是说，我们可以使用二分查找，将每一个数字的插入时间优化到O(logN)~~~~~于是算法的时间复杂度就降低到了O(NlogN)～！

package dp;

import java.util.Arrays;

public class LIS {

    public static int lis_lcs(int[] A) {
        int[] B = Arrays.copyOf(A, A.length);
        Arrays.sort(B);
        int[][] dp = new int[A.length+1][A.length+1];
        for (int i=1; i<=A.length; i++) {
            for (int j=1; j<=B.length; j++) {
                if (A[i-1] == B[j-1]) dp[i][j] = dp[i-1][j-1] +1;
                else dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return dp[A.length][B.length];
    }

    public static int lis_dp(int[] A) {
        int[] dp = new int[A.length];
        Arrays.fill(dp, 1);
        int lis = 0;
        for (int i=0; i<A.length; i++) {
            for (int j=0; j<i; j++) {
                if (A[i] > A[j] && dp[i]<dp[j]+1) {
                    dp[i] = dp[j] + 1;
                }
                if (lis < dp[i]) lis = dp[i];
            }
        }
        return lis;
    }

    public static int lis(int[] A) {
        if (A.length == 0) return 0;
        int[] B = new int[A.length];
        B[0] = A[0];
        int len = 1;
        for (int i=1; i<A.length; i++) {
            int left=0, right=len;
            while(left <= right) {
                int mid = (left + right) / 2;
                if (B[mid] < A[i]) left = mid + 1;
                else right = mid -1;
            }
            B[left] = A[i];
            if (left > len) len++;
        }
        return len;
    }

    public static void main(String[] args) {
        int[] a = {2, 1, 5, 3, 6, 4, 8, 9, 7};
        System.out.println(lis_lcs(a));
        System.out.println(lis_dp(a));
        System.out.println(lis(a));
    }

}

Felix’s Blog：最长递增子序列 O(NlogN)算法

最长公共子序列（LCS）和最长递增子序列（LIS）的求解