八大排序算法之四选择排序—堆排序(Heap Sort)
堆排序是一种树形选择排序,是对直接选择排序的有效改进。
基本思想:
堆的定义如下:具有n个元素的序列(k1,k2,...,kn),当且仅当满足
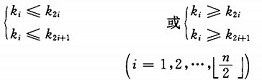
时称之为堆。由堆的定义可以看出,堆顶元素(即第一个元素)必为最小项(小顶堆)。 若以一维数组存储一个堆,则堆对应一棵完全二叉树,且所有非叶结点的值均不大于(或不小于)其子女的值,根结点(堆顶元素)的值是最小(或最大)的。如:
(a)大顶堆序列:(96, 83,27,38,11,09)
(b) 小顶堆序列:(12,36,24,85,47,30,53,91)
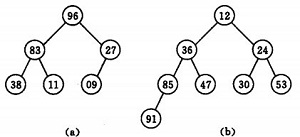
初始时把要排序的n个数的序列看作是一棵顺序存储的二叉树(一维数组存储二叉树),调整它们的存储序,使之成为一个堆,将堆顶元素输出,得到n 个元素中最小(或最大)的元素,这时堆的根节点的数最小(或者最大)。然后对前面(n-1)个元素重新调整使之成为堆,输出堆顶元素,得到n 个元素中次小(或次大)的元素。依此类推,直到只有两个节点的堆,并对它们作交换,最后得到有n个节点的有序序列。称这个过程为堆排序。
因此,实现堆排序需解决两个问题: 1. 如何将n 个待排序的数建成堆; 2. 输出堆顶元素后,怎样调整剩余n-1 个元素,使其成为一个新堆。
首先讨论第二个问题:输出堆顶元素后,对剩余n-1元素重新建成堆的调整过程。 调整小顶堆的方法:
1)设有m 个元素的堆,输出堆顶元素后,剩下m-1 个元素。将堆底元素送入堆顶((最后一个元素与堆顶进行交换),堆被破坏,其原因仅是根结点不满足堆的性质。
2)将根结点与左、右子树中较小元素的进行交换。
3)若与左子树交换:如果左子树堆被破坏,即左子树的根结点不满足堆的性质,则重复方法 (2).
4)若与右子树交换,如果右子树堆被破坏,即右子树的根结点不满足堆的性质。则重复方法 (2).
5)继续对不满足堆性质的子树进行上述交换操作,直到叶子结点,堆被建成。
称这个自根结点到叶子结点的调整过程为筛选。如图:
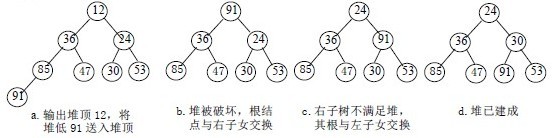
再讨论对n 个元素初始建堆的过程。 建堆方法:对初始序列建堆的过程,就是一个反复进行筛选的过程。
1)n 个结点的完全二叉树,则最后一个结点是第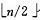 个结点的子树。
个结点的子树。
2)筛选从第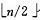 个结点为根的子树开始,该子树成为堆。
个结点为根的子树开始,该子树成为堆。
3)之后向前依次对各结点为根的子树进行筛选,使之成为堆,直到根结点。
如图建堆初始过程:无序序列:(49,38,65,97,76,13,27,49) 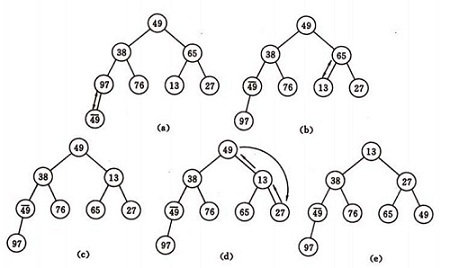

八大排序算法之四选择排序—堆排序(Heap Sort)的更多相关文章
- 八大排序算法~简单选择排序【记录下标k变量的作用】
八大排序算法~简单选择排序[记录下标k变量的作用] 1,思想:打擂台法,数组中的前n-1个元素依次上擂台"装嫩",后边的元素一个挨着一个不服,一个一个上去换掉它 2,优化:通过记录 ...
- Python排序算法之选择排序定义与用法示例
Python排序算法之选择排序定义与用法示例 这篇文章主要介绍了Python排序算法之选择排序定义与用法,简单描述了选择排序的功能.原理,并结合实例形式分析了Python定义与使用选择排序的相关操作技 ...
- 排序算法总结------选择排序 ---javascript描述
每当面试时避不可少谈论的话题是排序算法,上次面试时被问到写排序算法,然后脑袋一懵不会写,狠狠的被面试官鄙视了一番,问我是不是第一次参加面试,怎么可以连排序算法都不会呢?不过当时确实是第一次去面试,以此 ...
- 【DS】排序算法之选择排序(Selection Sort)
一.算法思想 选择排序是一种简单直观的排序算法.它的工作原理如下: 1)将序列分成两部分,前半部分是已经排序的序列,后半部分是未排序的序列: 2)在未排序序列中找到最小(大)元素,放到已排序序列的末尾 ...
- 八大排序算法之三选择排序—简单选择排序(Simple Selection Sort)
基本思想: 在要排序的一组数中,选出最小(或者最大)的一个数与第1个位置的数交换:然后在剩下的数当中再找最小(或者最大)的与第2个位置的数交换,依次类推,直到第n-1个元素(倒数第二个数)和第n个元素 ...
- 常用排序算法之——选择排序(C语言+VC6.0平台)
选择排序是另一种经典排序算法,核心思想是:在一趟找最小(大)数的过程中,先假设待排数据中的第一个数据即为最小(大)数据,然后循环将其他数据与该数据比较,每次比较时若小于该数据则让新数据成为最小(大)数 ...
- Java排序算法之选择排序
一.算法原理 简单选择排序的基本思想:给定数组:int[] arr={里面n个数据}:第1趟排序,在待排序数据arr[1]~arr[n-1]中选出最小的数据,将它与arrr[0]交换:第2趟,在待排序 ...
- 【排序算法】选择排序(Selection sort)
0. 说明 选择排序(Selection sort)是一种简单直观的排序算法. 它的工作原理如下. 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最 ...
- 我的Java开发学习之旅------>Java经典排序算法之选择排序
一.算法原理 对比数组中前一个元素跟后一个元素的大小,如果后面的元素比前面的元素小则用一个变量k来记住他的位置, 接着第二次比较,前面"后一个元素"现变成了"前一个元素& ...
随机推荐
- MySQL Server 5.6 配置文件my.ini 以及windows上mysql表名区分大小写
MySQL Server 5.6的配置文件my.ini的位置跟以往有所不同: 我的是在:C:\ProgramData\MySQL\MySQL Server 5.6\my.ini 前两天导sql 导完之 ...
- buffer cache中,各个object对象占用的buffer blocks
buffer cache中,各个object对象占用的buffer blocks: COLUMN OBJECT_NAME FORMAT A40 COLUMN NUMBER_OF_BLOCKS FORM ...
- Swift游戏实战-跑酷熊猫 02 创建熊猫类
要点: 如何继承SKSpriteNode :子类必须调用SKSpriteNode的一个指定构造器 init(){ super.init(texture:texture,color:UIColor.wh ...
- nyist 518 取球游戏
http://acm.nyist.net/JudgeOnline/problem.php?pid=518 取球游戏 时间限制:1000 ms | 内存限制:65535 KB 难度:2 描述 今 ...
- nyist 606 ACM之路
http://acm.nyist.net/JudgeOnline/problem.php?pid=606 ACM之路 时间限制:1000 ms | 内存限制:65535 KB 描述 转眼间,12级新生 ...
- c++的用处
C++准确说是一门中级语言,介于汇编和高级语言之间吧,要求程序员了解计算机的内部数据存储.个人认为,作为学生还是花功夫学C++,因为<设计模式><数据结构>这些课程基本上还是C ...
- paper 13:计算机视觉研究群体及专家主页汇总
做机器视觉和图像处理方面的研究工作,最重要的两个问题:其一是要把握住国际上最前沿的内容:其二是所作工作要具备很高的实用背景.解决第一个问题 的办法就是找出这个方向公认最高成就的几个超级专家(看看他们都 ...
- SQL Server数据库性能优化(一)之 优化SQL 语句
最近工作上基本没什么需求(好吧 不是最近是好久了,所以随便看看基础的东西来填补自己的空白) 原文出自:http://www.blogjava.net/allen-zhe/archive/2010/07 ...
- Jqueryの锋利的jquery练习
$(function(){ $("div.SubCategoryBox li:gt(7):not(:last)").hide(); $("div.SubCategoryB ...
- 解析xml文件
package com.ss1.xml; import java.io.File; import java.io.FileOutputStream; import java.io.IOExceptio ...
