Reservoir Sampling 蓄水池抽样算法，经典抽样

随机读取数据，如何保证真随机是不可能的，因为计算机的随机函数是伪随机的。

但是在不考虑计算机随机函数的情况下，如何保证数据的随机采样呢？

1.系统提供的shuffle函数

　　C++/Java都提供有shuffle函数，可以对容器内部的数据打乱，保持随机排序。

　　C++：

 template <class RandomAccessIterator, class URNG>
   void shuffle (RandomAccessIterator first, RandomAccessIterator last, URNG&& g);

　　Java：

 static void    shuffle(List<?> list);
 static void    shuffle(List<?> list, Random rnd);

　　这些函数对数量一定的数据的随机打乱顺序，并不能处理数量不定的数据流。

2.在序列流中取一个数，如何确保随机性，即取出某个数据的概率为:1/(已读取数据个数)

　　假设已经读取n个数，现在保留的数是A_x，取到A_x的概率为(1/n)。

　　对于第n+1个数A_n+1，以1/(n+1)的概率取A_n+1，否则仍然取A_x。依次类推，可以保证取到数据的随机性。

　　数学归纳法证明如下：

　　　　当n=1时，显然，取A₁。取A₁的概率为1/1。

假设当n=k时，取到的数据A_x。取A_x的概率为1/k。

当n=k+1时，以1/(k+1)的概率取A_n+1，否则仍然取A_x。

　　　　(1)如果取A_k+1，则概率为1/(k+1)；

　　　　(2)如果仍然取A_x，则概率为(1/k)*(k/(k+1))=1/(k+1)

　　所以，对于之后的第n+1个数A_n+1，以1/(n+1)的概率取A_n+1，否则仍然取A_x。依次类推，可以保证取到数据的随机性。

　　代码如下：

 //在序列流中取一个数，保证均匀，即取出数据的概率为:1/(已读取数据个数)
 void RandNum(){
     int res=;
     int num=;
     num=;
     cin>>res;

     int tmp;
     while(cin>>tmp){
         if(rand()%(num+)+>num)
             res=tmp;
         num++;
     }
     cout<<"res="<<res<<endl;
 }

3.在序列流中取k个数，如何确保随机性，即取出某个数据的概率为:k/(已读取数据个数)

　　建立一个数组，将序列流里的前k个数，保存在数组中。(也就是所谓的"蓄水池")

　　对于第n个数A_n，以k/n的概率取A_n并以1/k的概率随机替换“蓄水池”中的某个元素；否则“蓄水池”数组不变。依次类推，可以保证取到数据的随机性。

　　数学归纳法证明如下：

　　　　当n=k是，显然“蓄水池”中任何一个数都满足，保留这个数的概率为k/k。

假设当n=m(m>k)时，“蓄水池”中任何一个数都满足，保留这个数的概率为k/m。

当n=m+1时，以k/(m+1)的概率取A_n，并以1/k的概率，随机替换“蓄水池”中的某个元素，否则“蓄水池”数组不变。则数组中保留下来的数的概率为：

　

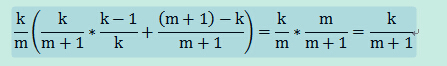
　　所以，对于第n个数A_n，以k/n的概率取A_n并以1/k的概率随机替换“蓄水池”中的某个元素；否则“蓄水池”数组不变。依次类推，可以保证取到数据的随机性。

　　代码如下：

 //在序列流中取n个数，保证均匀，即取出数据的概率为:n/(已读取数据个数)
 void RandKNum(int n){
     int *myarray=new int[n];
     for(int i=;i<n;i++)
         cin>>myarray[i];

     int tmp=;
     int num=n;
     while(cin>>tmp){
         if(rand()%(num+)+<n)
             myarray[rand()%n]=tmp;
     }

     for(int i=;i<n;i++)
         cout<<myarray[i]<<endl;
 }