Jacobi与SOR迭代法的实现与性能比较及均匀间距与Chebyshev插值的实现、性能分析及二者生成的插值误差比较

　　这篇文章给出（1）Jacobi与SOR迭代法的实现与性能比较及（2）均匀间距与Chebyshev插值的实现、性能分析及二者生成的插值误差比较，给出完整的实现代码，没有进行性能优化，仅供参考。

（1）Jacobi与SOR迭代法的实现与性能比较

一、举例计算

给出线性方程组：

　　其中n=100或者n=1000（任选一种，在本报告测试中，选取了n=100），使用Jacobi迭代法和SOR迭代法（=1,1.25,1.5）解此方程，计算结果精确到小数点后8位，结果输出小数点后至少12位，报告所需要的步数和误差（用无穷范数表示），比较计算结果。

二、Jacobi迭代法的实现

2.1、实现环境

MATLAB2018b

2.2、实现原理

　　整个Jacobi实现分下面几步实现：

　　首先需要给定这个系统的输入：矩阵A、向量b及初始向量x0，根据题目A与b是确定的，选定n=100，又矩阵A的是三对角矩阵，实现方式用到了MATLAB的内置函数diag来快速实现，具体实现如下：

　　A = diag(2*ones(100,1))+diag(ones(99,1),1)+diag(ones(99,1),-1);

而向量b直接取值即可，初始向量x0给定为：x0= 0.01*ones(100,1);

　　在确定好输入之后，其二需要给出Jacobi的运算方式，而其关键是计算向量的各个元素值，依据Jacobi的的计算公式：

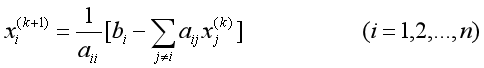
来进行运算，编写的函数在规定的迭代次数之前进行运算；

　　如果在规定的迭代次数之前所计算的误差精度大于规定的误差值时，即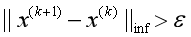或者，继续执行下面的步骤；

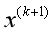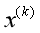　　在上一步结束之后‍需要更新的值，即的值赋给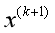，更新迭代的次数，之后再转到第二步继续循环运行，如此反复运行，直到结束。

2.3、数据测试

　　在n=100时，在MATLAB输入如下命令：function [y] = myJocobi(u_x0,u_A,u_b,S_error,N_times);而为了探讨经过Jacobi迭代运算之后误差的计算过程用二范数和无穷范数区别，特地做了实验来进行说明。当采用二范数时，计算结果如如图1所示：

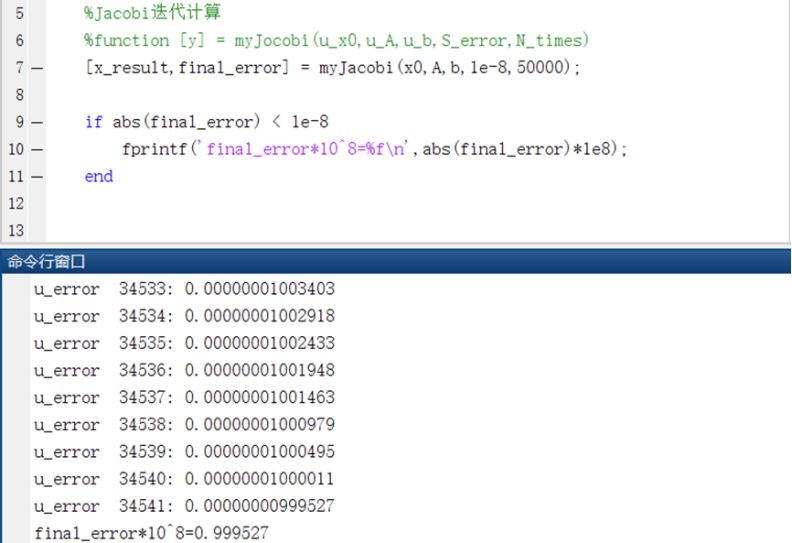
图1 Jacobi迭代结果（误差精度计算采用二范数)

　　当误差精度计算采用无穷范数时，计算结果如如图2所示：

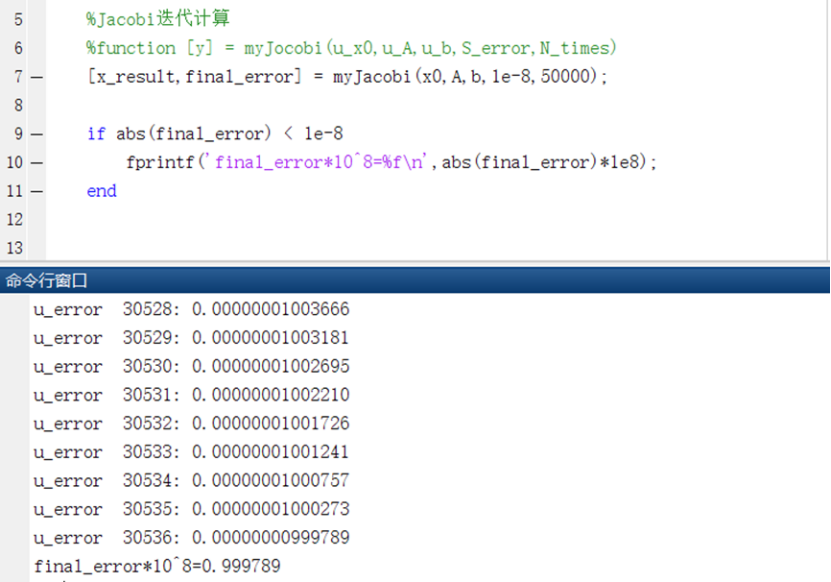
图2 Jacobi迭代结果（误差精度计算采用无穷范数)

2.4、数据分析

　　当n=100时，在实现精度等要求的前提下，误差精度计算采用二范数和无穷范数的Jacobi迭代的次数均达到3万多次，分别为34541及30536次，可以预测当n值取得很大的时候，Jacobi迭代效率会很低。

三、SOR迭代法的实现

3.1、实现环境

MATLAB2018b

3.2、实现原理

　　整个SOR迭代算法实现分下面几步实现：

　　首先需要给定这个系统的输入：矩阵A、向量b及初始向量x0，根据题目A与b是确定的，选定n=100，又矩阵A的是三对角矩阵，而相对于Jacobi迭代，SOR迭代多了一个超松弛因子w（w=1,1.25,1.5）。三对角矩阵A实现方式用到了MATLAB的内置函数diag来快速实现，具体实现如下：

A = diag(2*ones(100,1))+diag(ones(99,1),1)+diag(ones(99,1),-1);

而向量b直接依题取值即可，初始向量x0给定为：x0= 0.01*ones(100,1);

　　在确定好输入之后，其二需要给出SOR迭代的运算函数，而其关键是计算向量x的各个元素值x_i，依据SOR的的计算公式：

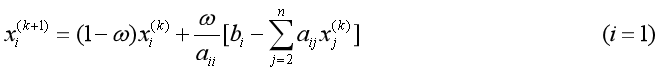
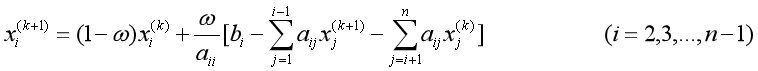
来进行运算，编写的函数在规定的迭代次数之前进行运算；

　　如果在规定的迭代次数之前所计算的误差精度大于规定的误差值时，即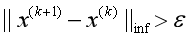,继续执行下面步骤；

　　在上一步结束之后‍需要更新的值，即的值赋给，更新迭代的次数，之后再转到第二步继续循环运行，如此反复运行，直到结束。

3.3、数据测试

　　在n=100时，在MATLAB输入如下命令：

　　[x_result,final_error] = mySOR(x0,A,b,1e-8,50000,1);

　　而为了探讨经过SOR迭代运算过程中超松弛因子w值不同对迭代的影响，现进行了w=1,1.25,1.5三次测试，测试结果如下：

n=100，超松弛因子=1时，SOR迭代结果如图3所示：

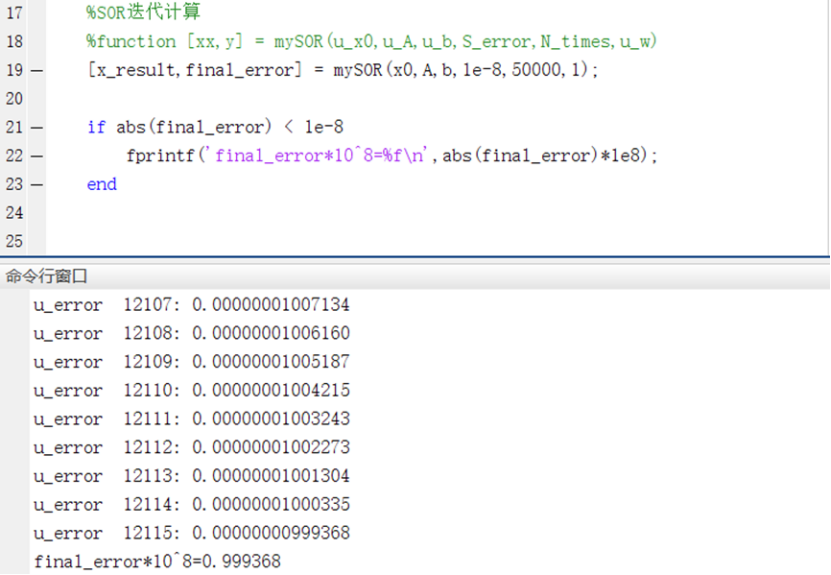
图3 超松弛因子=1时，SOR迭代结果

n=100，超松弛因子=1.25时，SOR迭代结果如图4所示：

图4 超松弛因子=1.25时，SOR迭代结果

n=100，超松弛因子=1.5时，SOR迭代结果如图5所示：

图5 超松弛因子=1.5时，SOR迭代结果

3.4、数据分析

　　当n=100时，在实现精度等要求的前提下，误差精度计算采用无穷范数的SOR迭代的次数在超松弛因子w分别取1、1.25、1.5时分别为12115、7584及4411次，可以看到，SOR迭代的整体速度较快，而在选取不同的超松弛因子值时，带来的最终结果却相差较大，因此可以预测当n值取得很大的时候，SOR迭代效率会比较高，且在选取合适的超松弛因子w时，效率提高会有数量级的提高。

四、Jacobi与SOR迭代法的运算结果比较

　　在前提条件相同的基础上，n=100时，Jacobi的迭代次数为34541及30536次，而SOR迭代的次数为12115、7584及4411次，误差精度计算采用无穷范数时，最大的次数比为30536/4411，比例约为7点多，可以看到Jacobi相比与SOR迭代在效率上差很多，而且随着n的增大，两者之间的效率会相差越来越明显。

（2）均匀间距与Chebyshev插值的实现、性能分析及二者生成的插值误差比较

一、举例计算

　　令f(x)=exp(|x|)，通过同时在区间[-1,1]上画出两种类型的n阶多项式，其中n(N)=10,20，比较均匀间距的插值和Chebyshev插值，对于均匀间距的插值，左右插值的基点为-1和1。以0.01的步长采样，对每种插值类型生成插值误差，并画出来进行比较，在这个问题里看是否能看到Runge现象。

二、均匀间距插值的实现

2.1、实现环境

MATLAB2018b

2.2、实现原理

　　在实验中，采用的是Lagrange来实现均匀间距插值和Chebyshev插值，实验中首先需要实现的就是Lagrange算法插值，对于n次的Lagrange插值，构造的基函数为：

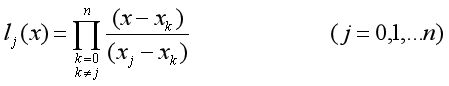
即得到满足插值条件：

得到插值函数为：

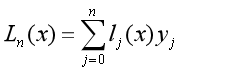
　　为了实现n=10,20的均匀间距插值，即对区间[-1,1]进行划相应的等分，核心实现为Lagrange函数，而Lagrange函数接口输入参数有三个，其一为[-1,1]区间中0.01步长得到的u_x，其二为经过均匀间距的变量值x_hk，其三为将划分的变量值经过函数y=exp(|x|)得到的输出值y_hk(hk =11对应n=10或者12对应n=20)，在Lagrange函数中，通过使用上文已经构造好的基函数及插值函数公式来进行计算，最后得到经过均匀间距插值的数据结果。

2.3、数据测试

　　在数据进行测试时，在MATLAB分别输入如下命令：

　　Ln1 = myLagrange(x11,y11,u_x);

　　Ln2 = myLagrange(x12,y12,u_x);

　　其中，x11与y11均为均匀间隔插值N(n)=10时，x12与y12均为均匀间隔插值N(n)=20时对数据的处理，最后得到结果如图6和图7所示，其中图6为将原函数与均匀间隔插值N(n)=10及均匀间隔插值N(n)=20图像分开比较，图7为三者一同进行比较：

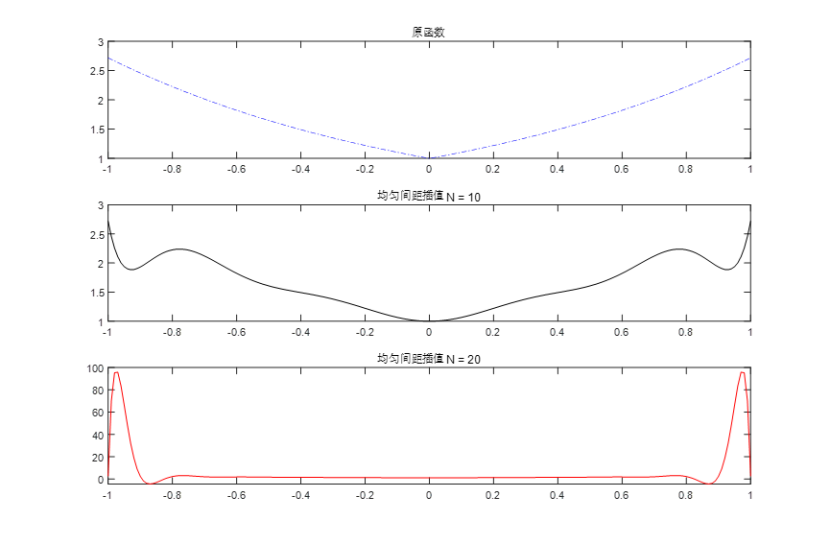
图6 均匀间隔插值与原函数进行比较-1

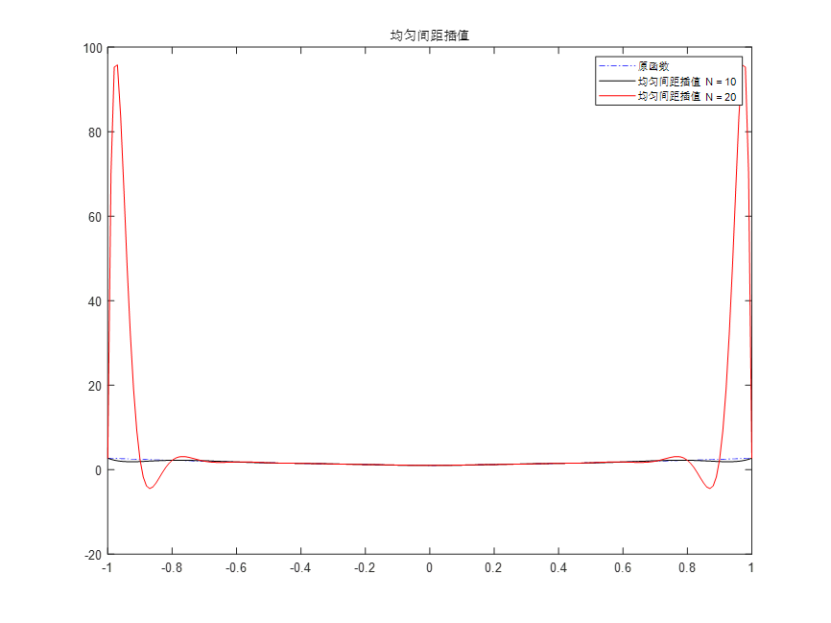
图7 均匀间隔插值与原函数进行比较-2

2.4、数据分析

　　从测试结果可以看到，使用均匀间隔插值的时候时可以逼近原函数的，但是存在当n太小的时候，插值函数整体上与原函数有一定的区别，但是在n增大的情况下，插值函数中间段部分与原函数逼近，但是两端出现了震荡，即出现了Runge现象。

三、Chebyshev插值的实现

3.1、实现环境

MATLAB2018b

3.2、实现原理

　　对于Chebyshev插值，其插值区间必须为[-1,1]，而题目是刚好吻合的，所以能够直接使用Chebyshev插值，而对于Chebyshev插值，选取的插值节点以如下公式进行计算：

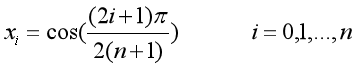
而在MATLAB中，向量的索引值从1开始，所以需要对公式进行变形，即：

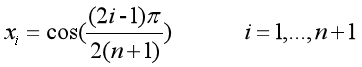
　　为了实现n=10,20的Chebyshev插值，即通过上面所列写的公式取节点值。同样Lagrange函数接口输入参数有三个，其一为[-1,1]区间中0.01步长得到的，其二为通过上面所列写的公式所取节点值x_hk，其三为将所取得节点值经过函数y=exp(|x|)得到的输出值y_hk(hk =21对应n=10或者22对应n=20)，在Lagrange函数中，通过使用上文已经构造好的基函数及插值函数公式来进行计算，最后得到经过Chebyshev插值的数据结果。

3.3、数据测试

　　在数据进行测试时，在MATLAB分别输入如下命令：

　　Ln3 = myLagrange(x21,y21,u_x);

　　Ln4 = myLagrange(x22,y22,u_x);

　　其中，x21与y21均为Chebyshev插值N(n)=10时，x22与y22均为Chebyshev插值N(n)=20时对数据的处理，最后得到结果如图8和图9所示，其中图8为将原函数与Chebyshev插值N(n)=10及Chebyshev插值N(n)=20图像分开比较，图9为三者一同进行比较：

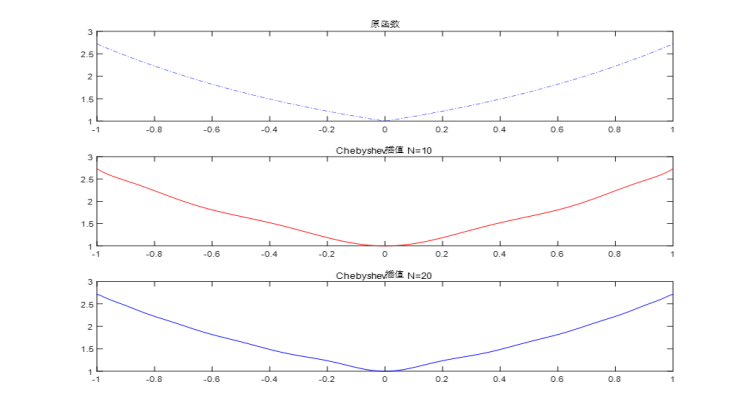
图8 Chebyshev插值与原函数进行比较-1

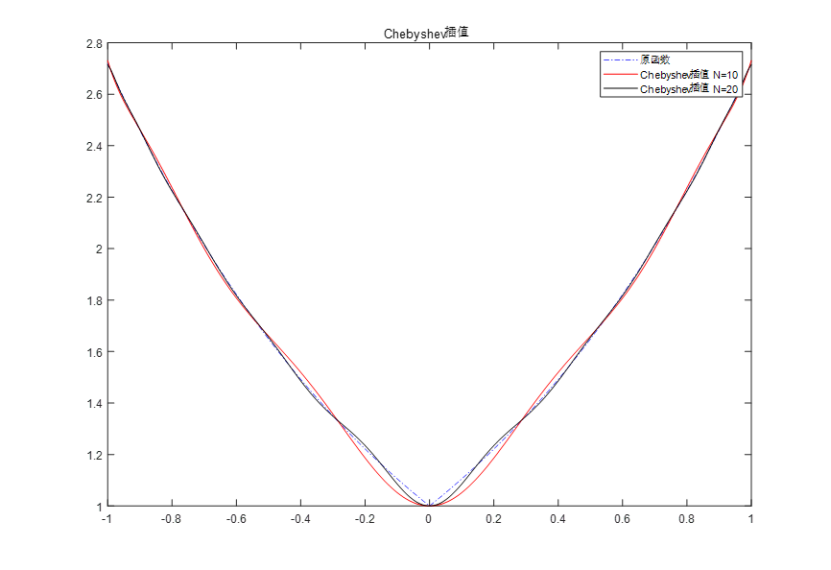
图9 Chebyshev插值与原函数进行比较-2

3.4、数据分析

　　从测试结果可以看到，使用Chebyshev插值的时候时可以更快地逼近原函数的，且当n比较小的时候，插值函数整体上与原函数区别不大。随着n的增大，插值函数与原函数越来越逼近，在误差允许情况下，能够很好的替换原函数，且避免了均匀间隔插值两端出现震荡的情况（Runge现象）。

四、均匀间距插值与Chebyshev插值误差比较

　　为了进行均匀间隔插值与Chebyshev插值误差比较，需要计算误差余项，通过对误差余项的定义得到余项的表达式：

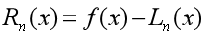
　　通过对误差余项的化简可以得到：

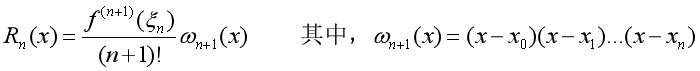
而在本次实验中f(x)=exp(|x|)，通过对化简，得到余项公式：

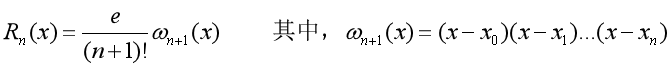
　　均匀间隔插值与Chebyshev插值通过计算化简后的余项即进行比较，其中在N(n)=10时，输入Rn_1 = myRn_solve(u_x,x11);

Rn_3 = myRn_solve(u_x,x21);

得到当前N(n)值时,间隔与Chebyshev插值误差，结果如图10所示：

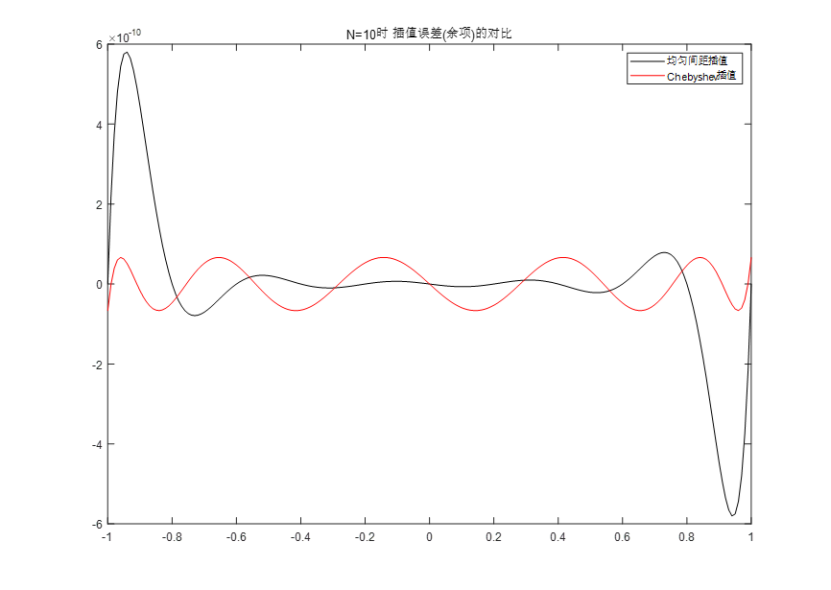
图10 n=10时，插值误差（余项）的对比

　　在N(n)=20时，输入Rn_2 = myRn_solve(u_x,x12);

　　　　　　　　　  Rn_4 = myRn_solve(u_x,x22);

得到当前N(n)值时,均匀间隔与Chebyshev插值误差，结果如图11所示：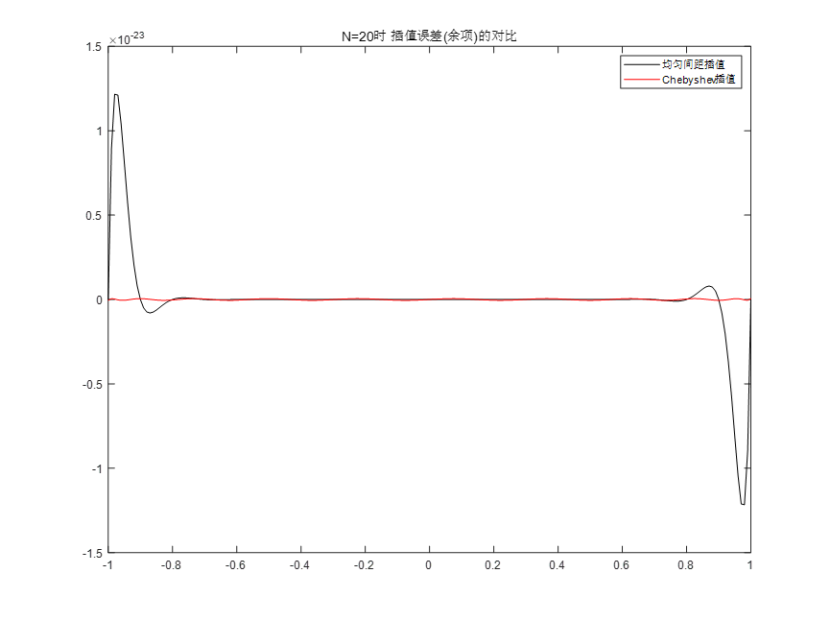

图11 n=20时，插值误差（余项）的对比

　　通过测试结果可以看出，在同一基础条件下，均匀间隔插值与Chebyshev插值的误差主要是在两端点处相差较大，而且随着n的增大，端点出的相差程度会更明显，从这也反映了均匀间隔插值带来的Runge现象影响。

附录

（1）Jacobi与SOR迭代法的实现代码

math_test.m

 1 %Jacobi迭代计算
 2 %function [y] = myJocobi(u_x0,u_A,u_b,S_error,N_times)
 3 % [x_result,final_error] = myJacobi(x0,A,b,1e-8,50000);
 4 %
 5 % if abs(final_error) < 1e-8
 6 %     fprintf('final_error*10^8=%f\n',abs(final_error)*1e8);
 7 % end
 8
 9
10
11
12
13 %SOR迭代计算
14 %function [xx,y] = mySOR(u_x0,u_A,u_b,S_error,N_times,u_w)
15 [x_result,final_error] = mySOR(x0,A,b,1e-8,50000,1);
16
17 if abs(final_error) < 1e-8
18     fprintf('final_error*10^8=%f\n',abs(final_error)*1e8);
19 end

myJacobi.m

 1 function [xx,y] = myJacobi(u_x0,u_A,u_b,S_error,N_times)
 2 %S_error 为规定的需要达到误差值
 3 %N_times 为规定的最大迭代次数
 4     u_count = 1;
 5     u_error = 1; %初始化默认误差为1
 6
 7     u_x = zeros(100,1); %初始化
 8     u_ax_toal = 0;
 9
10     while(abs(u_error) > S_error)
11
12
13
14         for i=1:100
15
16             for j=1:100
17                 if j ~= i  %如果 cnt不等于i
18                     u_ax = u_A(i,j)*u_x0(j);
19                     u_ax_toal = u_ax_toal + u_ax;
20                 end
21             end
22
23             u_x(i) = (u_b(i) - u_ax_toal)/u_A(i,i);
24             u_ax_toal = 0;
25         end
26
27
28         %u_error = norm(u_x-u_x0,2);   %求二范数
29         u_error = norm(u_x-u_x0,inf);   %求无穷范数
30
31         u_x0 = u_x;
32
33         if u_count>=N_times
34             break;
35         end
36
37         fprintf('u_error  %d: %16.14f\n',u_count,u_error);
38
39         u_count = u_count + 1;
40     end
41
42     y = u_error;
43     xx = u_x0;
44 end

mySOR.m

 1 function [xx,y] = mySOR(u_x0,u_A,u_b,S_error,N_times,u_w)
 2
 3 %S_error 为规定的需要达到误差值
 4 %N_times 为规定的最大迭代次数
 5     u_count = 1;
 6     u_error = 1; %初始化默认误差为1
 7
 8     u_x = zeros(100,1); %初始化
 9     u_ax_toal_last = 0;
10     u_ax_toal_now = 0;
11
12
13     while(abs(u_error) > S_error)
14
15         for i=1:100
16             if i==1
17                 for j=2:100
18
19                         u_ax = u_A(i,j)*u_x0(j);
20                         u_ax_toal_last = u_ax_toal_last + u_ax;
21                 end
22
23                 u_x(i) = (1-u_w)*u_x0(i) + u_w*((u_b(i) - u_ax_toal_last)/u_A(i,i));
24
25                 u_ax_toal_last = 0;
26             end
27
28             if i>=2 && i<=99
29                 for j=1:i-1
30
31                         u_ax = u_A(i,j)*u_x(j);
32                         u_ax_toal_now = u_ax_toal_now + u_ax;
33                 end
34
35                 for j=i+1:100
36
37                         u_ax = u_A(i,j)*u_x0(j);
38                         u_ax_toal_last = u_ax_toal_last + u_ax;
39                 end
40
41                 u_x(i) = (1-u_w)*u_x0(i) + u_w*((u_b(i) - u_ax_toal_last - u_ax_toal_now)/u_A(i,i));
42
43                 u_ax_toal_last = 0;
44                 u_ax_toal_now = 0;
45             end
46
47
48             if i==100
49                 for j=1:99
50
51                         u_ax = u_A(i,j)*u_x(j);
52                         u_ax_toal_now = u_ax_toal_now + u_ax;
53                 end
54
55                 u_x(100) = (1-u_w)*u_x0(100) + u_w*((u_b(100) - u_ax_toal_now)/u_A(100,100));
56
57                 u_ax_toal_now = 0;
58             end
59
60
61         end
62
63
64         %u_error = norm(u_x-u_x0,2);   %求二范数
65         u_error = norm(u_x-u_x0,inf);   %求无穷范数
66
67         u_x0 = u_x;
68
69         if u_count>=N_times
70             break;
71         end
72
73         fprintf('u_error  %d: %16.14f\n',u_count,u_error);
74
75         u_count = u_count + 1;
76     end
77
78     y = u_error;
79     xx = u_x0;
80 end

three_matrix.m

1 A = diag(2*ones(100,1))+diag(ones(99,1),1)+diag(ones(99,1),-1);
2
3 x0 = 0.01*ones(100,1);
4
5
6 b = zeros(100,0);
7 b(1) = 1;
8 b(100) = -1;
9 b = b';

（2）均匀间距与Chebyshev插值的实现

math_test_plot_Ln.m

 1 u_x = -1:0.01:1;
 2 u_y = exp(1).^abs(u_x);  % y = e^|x|
 3
 4
 5
 6 % %均匀间距插值，使用等间距节点作为插值节点
 7 % % title('均匀间距插值')
 8 %
 9 % %subplot(3,1,1);
10 % plot(u_x,u_y,'-.b')
11 % hold on
12 % %title('原函数')
13 % title('均匀间距插值')
14 %
15 %
16 % %subplot(3,1,2);
17 % x11 = -1:0.2:1; %n=10
18 % y11 = exp(1).^abs(x11);
19 % Ln1 = myLagrange(x11,y11,u_x);
20 % % Rn_1 = exp(1)*myRn_solve(u_x,x11);
21 % Rn_1 = myRn_solve(u_x,x11);
22 % plot(u_x,Ln1,'-k')
23 % % title('均匀间距插值 N = 10')
24 % hold on
25 %
26 % %subplot(3,1,3);
27 % x12 = -1:0.1:1; %n=20
28 % y12 = exp(1).^abs(x12);
29 % Ln2 = myLagrange(x12,y12,u_x);
30 % Rn_2 = myRn_solve(u_x,x12);
31 % plot(u_x,Ln2,'-r')
32 % % title('均匀间距插值 N = 20')
33 % hold on
34 %
35 % legend('原函数','均匀间距插值 N = 10','均匀间距插值 N = 20')
36
37
38
39
40 % %切比雪夫插值，使用切比雪夫节点作为插值节点
41 % subplot(3,1,1);
42 %
43 plot(u_x,u_y,'-.b')
44 % title(' 原函数 ')
45 hold on
46 title('Chebyshev插值 N=10');
47
48 % subplot(3,1,2);
49 x21 = myChebyshev(10);%n=10
50 y21 = exp(1).^abs(x21);
51 Ln3 = myLagrange(x21,y21,u_x);
52 Rn_3 = myRn_solve(u_x,x21);
53 plot(u_x,Ln3,'-r');
54 % title('Chebyshev插值 N=10');
55 hold on
56
57 % subplot(3,1,3);
58 x22 = myChebyshev(20);%n=20
59 y22 = exp(1).^abs(x22);
60 Ln4 = myLagrange(x22,y22,u_x);
61 Rn_4 = myRn_solve(u_x,x22);
62 plot(u_x,Ln4,'-b');
63 % title('Chebyshev插值 N=20');
64
65 legend('原函数','Chebyshev插值 N=10','Chebyshev插值 N=20')

math_test_plot_Rn.m

 1 u_x = -1:0.01:1;
 2 u_y = exp(1).^abs(u_x);  % y = e^|x|
 3
 4
 5
 6 % 均匀间距插值
 7
 8 x11 = -1:0.2:1; %n=10
 9 y11 = exp(1).^abs(x11);
10 Ln1 = myLagrange(x11,y11,u_x);
11 % Rn_1 = exp(1)*myRn_solve(u_x,x11);
12 Rn_1 = myRn_solve(u_x,x11);
13
14
15
16 x12 = -1:0.1:1; %n=20
17 y12 = exp(1).^abs(x12);
18 Ln2 = myLagrange(x12,y12,u_x);
19 Rn_2 = myRn_solve(u_x,x12);
20
21
22
23
24
25 % 切比雪夫插值，使用切比雪夫节点作为插值节点
26
27 x21 = myChebyshev(10);%n=10
28 y21 = exp(1).^abs(x21);
29 Ln3 = myLagrange(x21,y21,u_x);
30 Rn_3 = myRn_solve(u_x,x21);
31
32
33
34 x22 = myChebyshev(20);%n=20
35 y22 = exp(1).^abs(x22);
36 Ln4 = myLagrange(x22,y22,u_x);
37 Rn_4 = myRn_solve(u_x,x22);
38
39
40
41 %绘制插值余项的最大值
42 plot(u_x,Rn_1,'-k',u_x,Rn_3,'-r');
43 title('N=10时 插值误差(余项)的对比');
44 legend('均匀间距插值','Chebyshev插值');
45
46 % %绘制插值余项的最大值
47 % plot(u_x,Rn_2,'-k',u_x,Rn_4,'-r');
48 % title('N=20时 插值误差(余项)的对比');
49 % legend('均匀间距插值','Chebyshev插值');

myChebyshev.m

1 function x = myChebyshev(n)
2
3 x = zeros(1,n+1);
4 for k = 1:n+1
5     x(k) = cos(((2*k-1)*pi)/(2*(n+1)));  %此处从1开始，所以是2*k-1,否则为2*k+1
6 end

myLagrange.m

 1 function y = myLagrange(x0,y0,x)
 2 %f11 = myLagrange(x11,y11,u_x);
 3 % x11 = -1:0.2:1; %n=10
 4 % y11 = exp(1).^abs(x11);
 5
 6
 7 u_N=1:length(x0);
 8
 9
10
11 y=zeros(size(x));
12
13 for i=u_N
14     u_ij=find(u_N~=i);
15     y1=1;
16     for j=1:length(u_ij)
17         y1=y1.*(x-x0(u_ij(j)));
18     end
19
20     y2=1;
21     for j=1:length(u_ij)
22         y2=y2.*(x0(i)-x0(u_ij(j)));
23     end
24
25     y=y+y0(i)*y1/y2;
26
27 end

myRn_solve.m

 1 function u_Rn = myRn_solve(x,x0)
 2
 3 % x11 = -1:0.2:1; %n=10
 4 % y11 = exp(1).^abs(x11);
 5 % f11 = myLagrange(x11,y11,u_x);
 6 % Rn_1 = exp(1)*myRn_solve(u_x,x11);
 7
 8 u_Wn = zeros(1,length(x));
 9 u_Rn = zeros(1,length(x));
10 for i = 1:length(x)
11     u_Wn(i) = prod(x(i)*ones(1,length(x0))-x0);
12 end
13
14 u_Rn = u_Wn*exp(1)/factorial(length(x0));
15 end