洛谷 P1429 平面最近点对（加强版) (分治模板题)

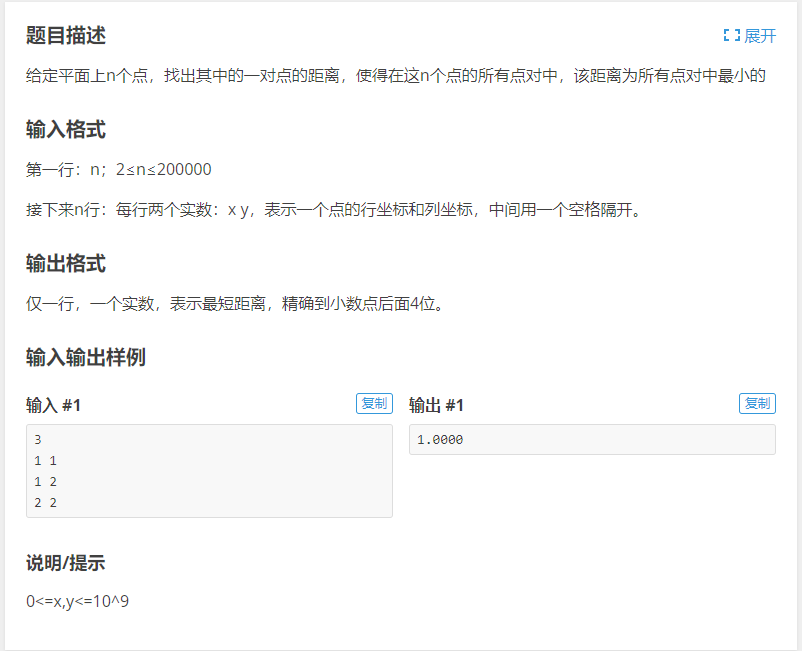
• 题意:有\(n\)个点对,找到它们之间的最短距离.

• 题解:我们先对所有点对以\(x\)的大小进行排序,然后分治,每次左右二等分递归下去,当\(l+1=r\)的时候,我们计算一下距离直接返回给上一层,若\(l==r\)说明只有一个点,不能构成线段,返回\(INF\),于是当前区间的左右两边的最短距离我们找到了,之后还有一种情况,就是一个点在\(mid\)左边,一个在\(mid\)右边,由于左右两边的最短距离\(d\)已知,所以我们可以再划分一个区间\([mid-d,mid+d]\),容易证明,若最短距离横穿\(mid\)线的话,两点一定在这个区间内,我们用\(tmp\)数组记录区间内的点,然后再枚举这些点求它们的距离,但是这里要优化一下,假如它们之间纵坐标的距离>\(d\),那么一定是不合法的,具体细节见代码.

• 代码:

  struct misaka{
  	double x,y;
  }e[N],tmp[N];
  
  int n;
  
  bool cmp1(misaka a,misaka b){
  	if(a.x==b.x) return a.y<b.y;
  	return a.x<b.x;
  }
  
  bool cmp2(misaka a,misaka b){
  	if(a.y==b.y) return a.x<b.x;
  	return a.y<b.y;
  }
  
  double dis(misaka a,misaka b){   //求距离
  	double res=fabs(a.x-b.x)*fabs(a.x-b.x)+fabs(a.y-b.y)*fabs(a.y-b.y);
  	return sqrt(res);
  }
  
  double MIN(double a,double b){  //手写求min
  	if(a>b) return b;
  	else return a;
  }
  
  double merge(int l,int r){
  	if(l==r) return INF;       //只有一个点
  	if(l+1==r) return dis(e[l],e[r]);   //递归边界,直接返回给上一层
  	int mid=(l+r)>>1;
  	int cnt=0;
  	double d=MIN(merge(l,mid),merge(mid+1,r));  //求左边和右边的最小距离
  	for(int i=l;i<=r;++i){
  		if(fabs(e[mid].x-e[i].x)<=d){        //判断点是否在[mid-x,mid+x]内
  			tmp[++cnt]=e[i];
  		}
  	}
  	sort(tmp+1,tmp+1+cnt,cmp2);			//按纵坐标排序
  	for(int i=1;i<=cnt;++i){
  		for(int j=i+1;j<=cnt && fabs(tmp[i].y-tmp[j].y)<=d;++j){    //若纵坐标的差大于d,直接下一个点
  			d=MIN(d,dis(tmp[i],tmp[j]));
  		}
  	}
  	return d;
  }
  
  int main() {
      //ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  	scanf("%d",&n);
  	for(int i=1;i<=n;++i) scanf("%lf %lf",&e[i].x,&e[i].y);
  
  	sort(e+1,e+1+n,cmp1);
  
  	double ans=merge(1,n);
  
  	printf("%.4f\n",ans);
  
      return 0;
  }