机器学习之shape

1. shape[:2] 取彩色图片的长和宽
   shape[:3]取彩色图片的长和宽和通道
   

2. img.shape[0]:图像的垂直高度
   img.shape[1]:图像的水平宽度
   img.shape[2]:图像的通道数
   

3. 矩阵中，[0]代表水平，[1]代表高度。
   

#示例代码
from skimage import io,data
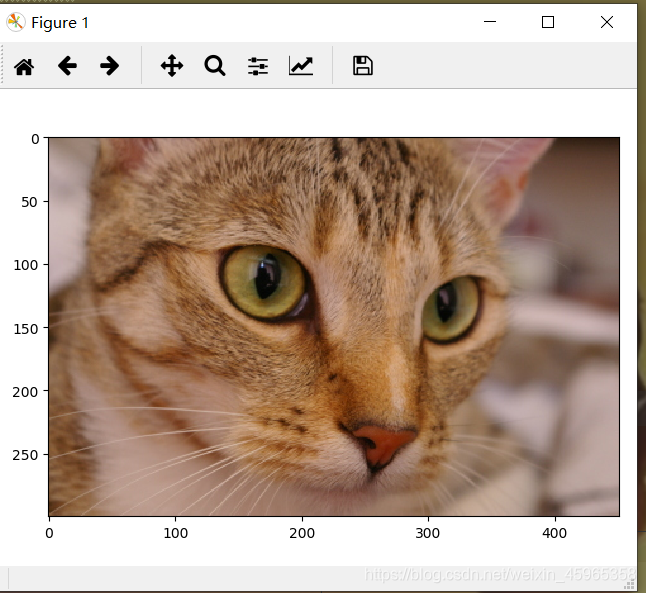
img = data.chelsea()
io.imshow(img)
io.imshow(img)
io.show()
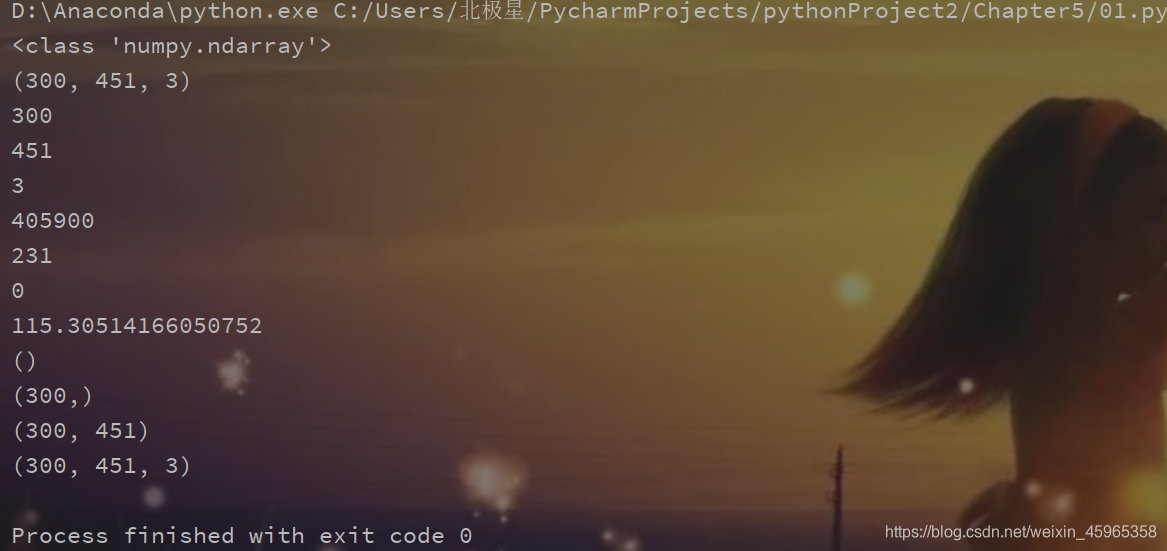
print(type(img))  #显示类型
print(img.shape)  #显示尺寸
print(img.shape[0])  #图片宽度
print(img.shape[1])  #图片高度
print(img.shape[2])  #图片通道数
print(img.size)   #显示总像素个数
print(img.max())  #最大像素值
print(img.min())  #最小像素值
print(img.mean()) #像素平均值
print(img.shape[:0])
print(img.shape[:1])#图片宽度
print(img.shape[:2])#图片宽度，高度
print(img.shape[:3])#图片宽度，高度，通道数

结果：