题解【NOIP2016】魔法阵

【NOIP2016】魔法阵

Description

六十年一次的魔法战争就要开始了，大魔法师准备从附近的魔法场中汲取魔法量。
大魔法师有m个魔法物品，编号分别为1,2,...,m。每个物品具有一个魔法值，我们用xi表示编号为i的物品的魔法值。每个魔法值xi是不超过n的正整数，可能有多个物品的魔法值相同。

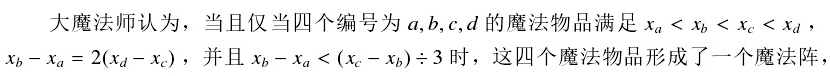
他称这四个魔法物品分别为这个魔法阵的A物品，B物品，C物品，D物品。
现在，大魔法师想要知道，对于每个魔法物品，作为某个魔法阵的A物品出现的次数，作为B物品的次数，作为C物品的次数，和作为D物品的次数。

Input

第一行包含两个空格隔开的正整数n和m
接下来m行，每行一个正整数，第i+1行的正整数表示x}，即编号为i的物品的魔法值。
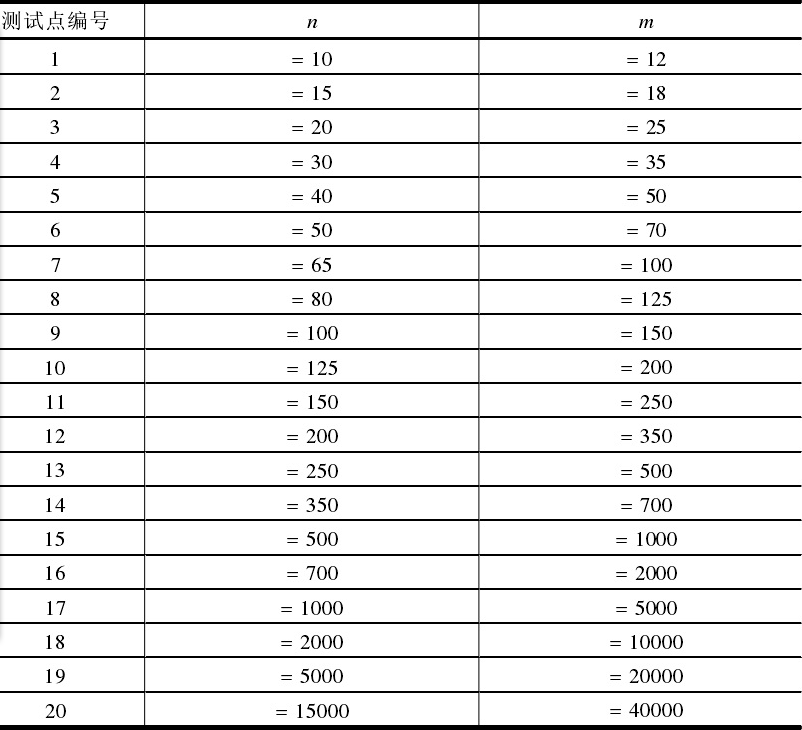
保证1 <= n <= 15000,1 <= m <= 40000,1 <= xi <= n。每个xi是分别在合法范围内等概率随机生成的。

Output

共输出m行，每行四个整数。第i行的四个整数依次表示编号为i的物品作为A,B,C,D物品分别出现的次数。
保证标准输出中的每个数都不会超过10^9
每行相邻的两个数之间用恰好一个空格隔开。

Sample Input

输入样例1：
30 8
1
24
7
28
5
29
26
24

输入样例2：
15 15
1
2
3
4
5
6
7
8
9
1
11
12
13
14
15

Sample Output

输出样例1：
4 0 0 0
0 0 1 0
0 2 0 0
0 0 1 1
1 3 0 0
0 0 2 0
0 0 2 2
0 0 1 0

输出样例2：
5 0 0 0
4 0 0 0
3 5 0 0
2 4 0 0
1 3 0 0
0 2 0 0
0 1 0 0
0 0 0 0
0 0 0 0
0 0 1 0
0 0 2 1
0 0 3 2
0 0 4 3
0 0 5 4
0 0 0 5

Hint

输入样例1提示：
共有5个魔法阵，分别为:
物品1,3,7,6，其魔法值分别为1, 7, 26, 29;
物品1,5,2,7，其魔法值分别为1, 5, 24, 26;
物品1,5,7,4，其魔法值分别为1, 5, 26, 28;
物品1,5,8,7，其魔法值分别为1, 5, 24, 26;
物品5,3,4,6，其魔法值分别为5, 7, 28, 29 0
以物品_5为例，它作为A物品出现了1次，作为B物品出现了3次，没有作为C物品或者D物品出现，所以这一行输出的四个数依次为1,3,0,0 0
此外，如果我们将输出看作一个m行4列的矩阵，那么每一列上的m个数之和都应等于魔法阵的总数。所以，如果你的输出不满足这个性质，那么这个输出一定不正确。你可以通过这个性质在一定程度上检查你的输出的正确性。

数据范围：

Source

NOIP2016普及组
动态规划

解析

这题用暴力特别好写。

但时间复杂度会炸啊啊啊！！！

所以我们要考虑优化。

首先，想想n是干什么的？

没错，我们可以用桶排！

用d[i]记录i魔法值为i的物品个数。

然后，再考虑一下解法：

先看下图（图片来自网络（真的画不出来））：

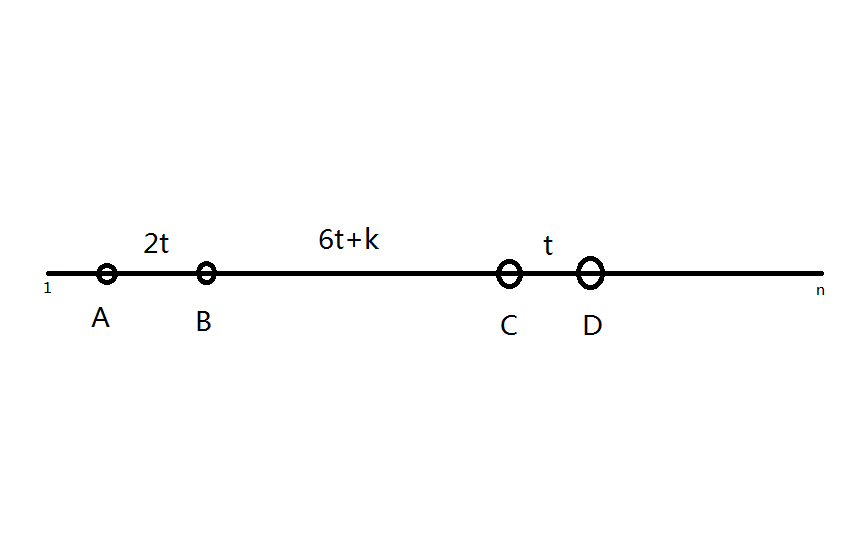
当d-c等于t时，各点之间的距离就如上图。

所以，确定d的位置后，c的位置也就确定了。

而对于一对确定的c,d，

能够于它们组成魔法阵的a,b的组数为∑（d[ai]*d[bi]）(ai,bi为满足条件的魔法值)。

因此，我们还能用前缀和优化。

因为当t一定时，若一对（a,b）满足条件，则a,b之前的所有差值为2×t的魔法值都一定满足条件。

最后，c的组数就等于（a,b的组数）×魔法值为d的物品个数（d也一样）。

于是我们枚举d的值，再一边递推就行了。

最后，同理，枚举a的位置，计算满足条件的c,d组数，就可以AC了！（注意，a要倒着枚举，因为c,d是从后往前递推的。）

上AC代码（如果前面不太懂可以看代码理解）：

#include <bits/stdc++.h>

using namespace std;

int n,m;

int a[];

int f[][]/*作为第i个物品时,魔法值为j的次数*/;

int d[]/*魔法值为i的物品个数*/;

int sum=,cnt=;

int main(){

    memset(f,,sizeof(f));

    scanf("%d%d",&n,&m);

    for(int i=;i<=m;i++){

        scanf("%d",&a[i]);

        d[a[i]]++;

    }

    for(int t=;t*+<=n;t++){

        sum=;cnt=;

        for(int dd=*t+;dd<=n;dd++){

            int cc=dd-t;//第三个物品

            int bb=cc-*t-;//第二个物品

            int aa=bb-*t;//第一个物品

            sum+=d[aa]*d[bb];//递推计算前缀和

            f[][cc]+=sum*d[dd];//魔法值为d的个数可能不是/不止1个

            f[][dd]+=sum*d[cc];//同理

        }

        for(int aa=n-*t-;aa>=;aa--){

            int bb=aa+*t;//第二个物品

            int cc=bb+*t+;//第三个物品

            int dd=cc+t;//第四个物品

            cnt+=d[cc]*d[dd];

            f[][aa]+=cnt*d[bb];

            f[][bb]+=cnt*d[aa];

        }

    }

    for(int i=;i<=m;i++){

        for(int j=;j<=;j++){

            printf("%d ",f[j][a[i]]);

        }

        printf("\n");

    }

    return ;

}