CSP-S 模拟测试 51 题解

考试过程：

惯例先看一遍三道题，T1 一开始反应要求割点，但是这是有向图，肯定不能求割点，康了一下数据范围，有40%是树的，还不错，决定待会在打。

看T2 字符串题，完了我字符串最弱了，肯定只能打暴力了，带着前两题都不会的心情，看了T3发现是期望，完了爆0了，在一看，发现是sb原题，还简单一点，赶紧把T3码了一遍过大样例，觉得很稳就交了，然后用一点时间把T1树的分给码了，然后开始磨T2，发现啥都不会开始dfs，一开始觉得只能拿30pts，后来发现没有回溯是$O(n^2)$的，打完就没剩多少时间了，然后考虑T3要不要开long long，觉得没必要就没开石乐智。然后想T1无果。

出分发现T3WA 80，然后把开了long long的代码交上去A了，我怕不是个傻子，不卡时间为什么不开long long啊QAQ。T2A了，T140，后来听说用树的方法跑所有测试点能拿60，艹。少两句话少拿40.jpg。

扯多了2333

题解：

T1 attack：

据说是什么支配树裸题，蒟蒻不会，只能照着题解打。

必经关系是一棵树，这好像就是支配树？那么1到k的必经点就是k在这棵树上的祖先，所以我们在有向图中跑个拓扑排序，就可以建出这棵树，但实际上我们并不需要真正建出这棵树，只需要维护求lca所用的fa数组和dep数组即可。另外，因为题目中说所有点都从1开始，所以一开始只要把1入队就吼了。

再说一下我的sb手残错误

求lca：

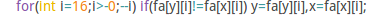我是大设备

 #include<bits/stdc++.h>
 using namespace std;
 const int N=1e5+;
 const int INF=1e9+;
 int first[N],nex[N<<],to[N<<],tot;
 void add(int a,int b){
     to[++tot]=b,nex[tot]=first[a],first[a]=tot;
 }
 vector<int> in[N];
 int d[N],du[N],fa[N][],v[N],w[N];
 int Lca(int x,int y){
     if(d[x]>d[y]) swap(x,y);
     for(int i=;i>=;--i) if(d[fa[y][i]]>=d[x]) y=fa[y][i];
     if(x==y) return x;
     for(int i=;i>=;--i) if(fa[y][i]!=fa[x][i]) y=fa[y][i],x=fa[x][i];
     return fa[x][];
 }

 int main(){
     int n,m,que;
     scanf("%d%d%d",&n,&m,&que);
     for(int i=;i<=m;++i){
         int x,y;
         scanf("%d%d",&x,&y);
         add(x,y);
         add(y,x);
         in[y].push_back(x);
         du[y]++;
     }
     queue<int> q;
     q.push();
 //    d[1]=0;
     /*for(int i=1;i<=n;++i){
         if(!du[i]){
             int lca=in[i][0];
             for(int j=1;j<in[i].size();++j) lca=Lca(lca,in[i][j]);
             fa[i][0]=lca;
             d[i]=d[lca]+1;
             for(int j=1;j<=16;++j) fa[i][j]=fa[fa[i][j-1]][j-1];
             q.push(i);
             v[i]=1;
         }
     }*/
     // for(int i=1;i<=n;++i) if(!du[i]) q.push(i)/*,du[i]=INF*/;
     while(q.size()){
         int x=q.front();q.pop();//cout<<x<<endl;
         for(int i=first[x];i;i=nex[i]){
             int y=to[i];
             du[y]--;
             if(!du[y]){
                 int lca=in[y][];
                 for(int j=;j<in[y].size();++j) lca=Lca(lca,in[y][j]);
                 fa[y][]=lca;
                 d[y]=d[lca]+;
                 q.push(y);
 //                du[i]=INF;
                 for(int j=;j<=;++j) fa[y][j]=fa[fa[y][j-]][j-];
             }
         }
     }
 //    for(int i=1;i<=n;++i,cout<<endl) for(int j=1;j=16;++j) cout<<fa[i][j]<<" ";
     for(int i=;i<=que;++i){
         int k;
         scanf("%d",&k);
         for(int j=;j<=k;++j) scanf("%d",&w[j]);
         int lca=w[];
         for(int j=;j<=k;++j) lca=Lca(lca,w[j]);
         printf("%d\n",d[lca]+);
     }
 }
 /*
 4 3 2
 1 2
 2 3
 2 4
 2 3 4
 2 2 4
 */

attack

T2 reverse：

只需要考虑最后一位是什么就好了，然后谁长就缩谁，直到他们两个一样长，就一起缩，博主打的是dfs，细节很多，很难调，所以代码就不提供了，所以就以soul神的代码为参考吧。

鸣谢soul

 #include<bits/stdc++.h>
 #define re register
 using namespace std;
 int T,a[],b[]; char s[]; int len;
 inline bool cmp(){
     if(a[]!=b[]) return ;
     for(re int i=;i<=a[];++i)
         if(a[i]!=b[i]) return ;
     return ;
 }
 signed main(){
     scanf("%d",&T);
     while(T--){
         scanf("%s",s+);len=strlen(s+); a[]=;
         for(re int i=;i<=len;++i) a[++a[]]=(s[i]-);
         scanf("%s",s+);len=strlen(s+); b[]=;
         for(re int i=;i<=len;++i) b[++b[]]=(s[i]-);
         while(a[]&&b[]&&!cmp()){
             if(a[]>b[])
                 while(a[]>b[]){
                     if(a[a[]--])
                     for(re int i=,lim=(a[]>>);i<=lim;++i) swap(a[i],a[a[]-i+]);
                 }
             else if(a[]<b[])
                 while(b[]>a[]){
                     if(b[b[]--])
                     for(re int i=,lim=(b[]>>);i<=lim;++i) swap(b[i],b[b[]-i+]);
                 }
             else if(a[]==b[]){
                 if(a[a[]--])
                 for(re int i=,lim=(a[]>>);i<=lim;++i) swap(a[i],a[a[]-i+]);
                 if(b[b[]--])
                 for(re int i=,lim=(b[]>>);i<=lim;++i) swap(b[i],b[b[]-i+]);
             }
         }
         if(a[]){for(re int i=;i<=a[];++i) putchar(a[i]+); puts("");}
         else puts("-1");
     }
     return ;
 }

reverse

T3 tree：

原题，不，比原题简单，然后赛时第一个提交，成功long long见祖宗，喜提WA80。

题解是什么方法我也不知道，所以就用自己的方法说了还不是颓的以前的题解。

我们设$f[x]$表示从$x$到$fa[x]$的期望步数，$g[x]$表示从$fa[x]$到$x$的期望步数。

考虑转移$f[x]=\frac{1}{du[x]}+\sum{\frac{f[son]+1+f[x]}{du[x]}}$

挺显然的，就是他可以直接上去，也可能先下去在上去。

化简得$f[x]=du[x]+\sum{f[son]}$，一遍dfs可以求出

在来考虑g的转移$g[x]=\frac{1}{du[fa]}+\frac{1+g[x]+g[fa]}{du[fa]}+\frac{\sum{g[x]+1+f[brothers]}}{du[fa]}$

其实和f的转移也差不多就是分类讨论，可以直接下去，可以到x的兄弟节点也可以到x的父节点的父节点。

化简得$g[x]=du[fa]+g[fa]+\sum{f[bother]}$

然后树上前缀和就可以求出从根到x的期望步数了。

吐槽：

考试时知道答案一定是整数就没开double，然后，关于int，他死了最后都想到开long long了为什么不交啊，我的首杀。

 //yuanti
 //xingkuizuoguo
 #include<bits/stdc++.h>
 using namespace std;
 const int N=1e5+;
 #define int long long
 int first[N],nex[N<<],to[N<<],tot;
 void add(int a,int b){
     to[++tot]=b,nex[tot]=first[a],first[a]=tot;
 }
 int f[N],g[N];//f[x] x->fa[x] g[x] fa[x]->x
 int sumg[N],sumf[N];
 int du[N];
 void dfs(int x,int fa){
     f[x]=du[x];
     for(int i=first[x];i;i=nex[i]){
         int y=to[i];
         if(y==fa) continue;
         dfs(y,x);
         f[x]+=f[y];
     }
     sumf[x]=f[x];
 }
 void dfs1(int x,int fa){
     for(int i=first[x];i;i=nex[i]){
         int y=to[i];
         if(y==fa) continue;
         g[y]=sumf[x]-f[y]+g[x];
         dfs1(y,x);
     }
 }
 void dfs2(int x,int fa){//cout<<fa<<" "<<g[fa]<<" "<<sumg[fa]<<endl;
     sumg[x]=sumg[fa]+g[x];
     for(int i=first[x];i;i=nex[i]){
         int y=to[i];
         if(y==fa) continue;
         dfs2(y,x);
     }
 }

 signed main(){
     int n;
     scanf("%lld",&n);
     for(int i=;i<n;++i){
         int x,y;
         scanf("%lld%lld",&x,&y);
         add(x,y);
         add(y,x);
         du[x]++;du[y]++;
     }
     dfs(,);
     f[]=;
     dfs1(,);
     sumg[]=g[];
     dfs2(,);
 //    for(int i=1;i<=n;++i) cout<<"f["<<i<<"]=="<<f[i]<<" ";
 //    cout<<endl;
 //    for(int i=1;i<=n;++i) cout<<"g["<<i<<"]=="<<g[i]<<" ";
 //    cout<<endl;
     for(int i=;i<=n;++i){
         printf("%lld.000\n",sumg[i]+);
     }
 }
 /*
  3
  1 2
  2 3
 */

tree