[2019南昌邀请赛网络赛D][dp]

https://nanti.jisuanke.com/t/38223

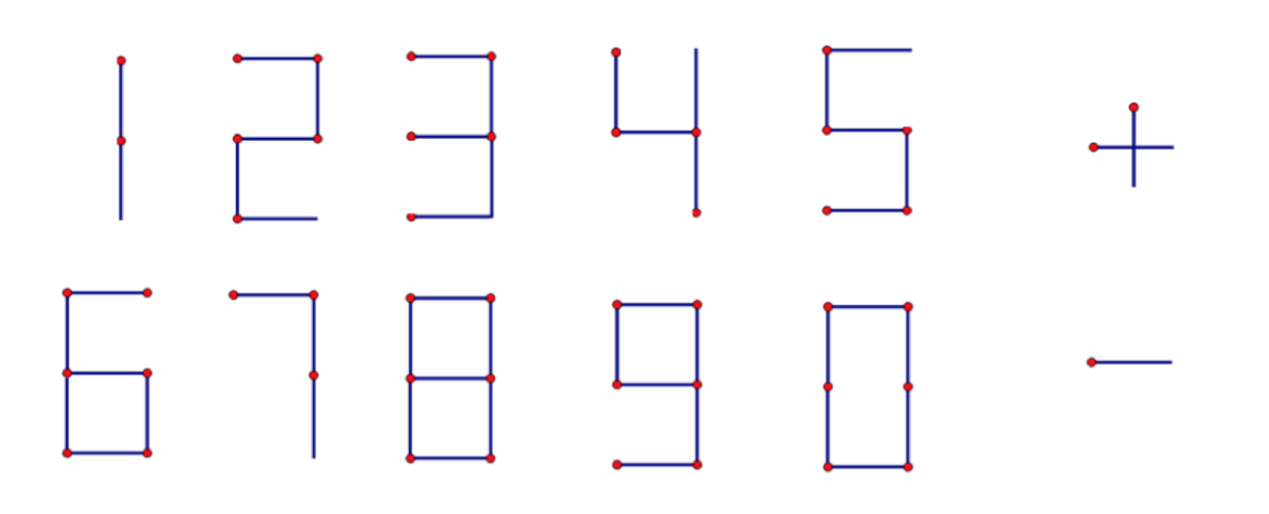
Xiao Ming recently indulges in match stick game and he thinks he is good at it. His friend Xiao Jun decides to test him. Xiao Jun gives him an expression of length , made by match sticks and asks him to calculate the maximum value of the expression by moving any match sticks (but he can’t discard any of them). The expression is made up of some numbers, plus signs and minus signs represented as A_1 \ op_1 \ A_2 \ op_2 \ A_3 \ op_3 \ \cdots A_{m - 1} \ op_{m - 1} \ A_mA1​ op1​ A2​ op2​ A3​ op3​ ⋯Am−1​ opm−1​ Am​. mm must be count by himself, A_k(1 \le k \le m)Ak​(1≤k≤m) is an integer without leading zeros and less than 10^9109 , op_k (1 \le k \le m)opk​(1≤k≤m) is a plus sign or a minus sign. At the same time, there are some requirements of the new expression:

1. The new expression should also be made up of mm numbers and m - 1m−1 operators.
2. The number of digits per number should keep consistent with the original.
3. There couldn’t be any leading zeros per number.

Input

The first line consists of a single integer TTdenoting the number of test cases.

There’re two lines in each test case.

The first line contains an integer nn.

A string of length nn follows in the next line, denoting the expression given.

The expression is guaranteed to be valid.

Output

For each test case, print a single integer denoting the maximum result of the expression.

Constraints

1 \le n \le 1001≤n≤100

Note

Expression with the maximum result for the second sample is 7 - 17−1 .

Expression with the maximum result for the second sample is 7 + 7 + 97+7+9.

样例输入复制

3
3
1-1
3
1+1
5
1+2+3

样例输出复制

0
6
23
题意：给出每个数字和加号减号需要的火柴数，然后给出t组多项式，求不改变多项式项数以及每项数字位数的前提下得到的多项式的最大值
题解：由于不存在括号而且加法和减法是同级运算，所以这个求解过程满足dp的子问题性质，可以使用dp解决，由于项数以及位数不能变，所以先dp出i个火柴能拼出的j位最大值和最小值，然后dp枚举每一项的前面的符号是+还是-,是加法就使用i火柴能拼出j位数字的最大值更新dp数组，否则就使用最小值更新

 #include<iostream>
 #include<vector>
 #include<cstring>
 #include<cstdio>
 #include<queue>
 #include<map>
 using namespace std;
 char ch[];
 map<char,int>mp;
 typedef long long ll;
 int q[];
 ll dp[][],dp2[][],dp3[][];
 vector<int>g[];
 int main(){
     int t;
     scanf("%d",&t);
     g[].push_back();
     mp['']=;
     g[].push_back();
     mp['']=;
     g[].push_back();
     mp['']=;
     g[].push_back();
     mp['']=;
     g[].push_back();
     mp['']=;
     g[].push_back();
     mp['']=;
     g[].push_back();
     mp['']=;
     g[].push_back();
     mp['']=;
     g[].push_back();
     mp['']=;
     g[].push_back();
     mp['']=;
     mp['+']=;
     mp['-']=;
     memset(dp2,-,sizeof(dp2));
     memset(dp3,-,sizeof(dp3));
     dp2[][]=;
     for(int i=;i<=;i++){
         for(int j=;j<=;j++){
             for(int k=;k<;k++){
             if(dp2[i-j][k-]!=-&&i>=j)dp2[i][k]=max(dp2[i-j][k-]*+g[j][g[j].size()-],dp2[i][k]);
            // if(dp2[i-j]!=-1&&dp2[i][k]==-1&&i>=j)dp2[i][k]=dp2[i-j][k-1]*10+g[j][g[j].size()-1];
             }
         }
     }
     dp3[][]=;
     for(int i=;i<=;i++){
         for(int j=;j<=;j++){
             for(int k=;k<;k++){
                 if(dp3[i-j][k-]!=-&&i>=j)dp3[i][k]=min(dp3[i-j][k-]*+g[j][],dp3[i][k]);
                 if(dp3[i-j][k-]!=-&&dp3[i][k]==-&&i>=j)dp3[i][k]=dp3[i-j][k-]*+g[j][];
             }
         }
     }
     //for(int i=1;i<=12;i++)cout<<dp2[i]<<endl;
     while(t--){
         int n;
         scanf("%d",&n);
         scanf("%s",ch);
         int tot=;
         ll sum=;
         int f=;
         for(int i=;i<n;i++){
             if(ch[i]=='+'||ch[i]=='-'){tot++;q[tot]=i-f;f=i+;}
             sum+=mp[ch[i]];
         }
         q[++tot]=n-f;
         memset(dp,-,sizeof(dp));
         dp[][]=;
        // cout<<sum<<endl;
         for(int i=;i<=tot;i++){
             for(int j=;j<=sum;j++){
                 for(int k=;k<=;k++){
                     //cout<<dp2[k][q[i]]<<endl;
                     if(i>&&j-k->=&&dp[i-][j-k-]!=-&&dp2[k][q[i]]!=-)dp[i][j]=max(dp[i-][j-k-]+dp2[k][q[i]],dp[i][j]);
                     if(i==&&j-k>=&&dp[i-][j-k]!=-&&dp2[k][q[i]]!=-)dp[i][j]=max(dp[i-][j-k]+dp2[k][q[i]],dp[i][j]);
                     if(j-k->=&&dp[i-][j-k-]!=-&&dp3[k][q[i]]!=-)dp[i][j]=max(dp[i-][j-k-]-dp3[k][q[i]],dp[i][j]);
                     if(dp[i][j]==-){
                         if(i>&&j-k->=&&dp[i-][j-k-]!=-&&dp2[k][q[i]]!=-){
                             dp[i][j]=dp[i-][j-k-]+dp2[k][q[i]];
                         }
                         if(i==&&j-k>=&&dp[i-][j-k]!=-&&dp2[k][q[i]]!=-){
                             dp[i][j]=dp[i-][j-k]+dp2[k][q[i]];
                         }
                         if(j-k->=&&dp[i-][j-k-]!=-&&dp3[k][q[i]]!=-){
                             dp[i][j]=dp[i-][j-k-]-dp3[k][q[i]];
                         }
                     }
                 }
             }
         }
         printf("%lld\n",dp[tot][sum]);
     }
     return ;
 }