poj 1279 -- Art Gallery (半平面交)
鏈接:http://poj.org/problem?id=1279
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 5337 | Accepted: 2277 |
Description
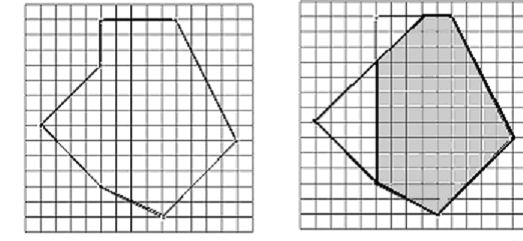
Input
Output
Sample Input
1
7
0 0
4 4
4 7
9 7
13 -1
8 -6
4 -4
Sample Output
80.00
Source
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm> #define eps 1e-8
#define MAXX 1510 typedef struct point
{
double x;
double y;
}point; point p[MAXX],s[MAXX]; using namespace std;
bool dy(double x,double y)
{
return x>y+eps;
}
bool xy(double x,double y)
{
return x<y-eps;
}
bool dyd(double x,double y)
{
return x>y-eps;
}
bool xyd(double x,double y)
{
return x<y+eps;
}
bool dd(double x,double y)
{
return fabs(x-y)<eps;
} double crossProduct(point a,point b,point c)
{
return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x);
} point IntersectPoint(point u1,point u2,point v1,point v2)
{
point ans=u1;
double t = ((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x))/
((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));
ans.x += (u2.x-u1.x)*t;
ans.y += (u2.y-u1.y)*t;
return ans;
} double Area(point p[],int n)
{
double ans=0.0;
for(int i=; i<n-; i++)
{
ans += crossProduct(p[],p[i],p[i+]);
}
return fabs(ans)/2.0;
} double dist(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
} bool cmp(point a,point b)
{
double tmp=crossProduct(p[],a,b);
if(dd(tmp,0.0))
return dy(dist(p[],a),dist(p[],b));
return xy(tmp,0.0);
} point Getsort(int n)
{
int tmp=;
for(int i=; i<n; i++)
{
if(xy(p[i].x,p[tmp].x) || dd(p[i].x,p[tmp].x)&&xy(p[i].y,p[tmp].y))
{
tmp=i;
}
}// printf("%d^^",tmp);
swap(p[],p[tmp]);
sort(p+,p+n,cmp);
} void cut(point p[],point s[],int n,int &len)
{
point tp[MAXX];
p[n]=p[];
for(int i=; i<=n; i++)
{
tp[i]=p[i];
}
int cp=n,tc;
for(int i=; i<n; i++)
{
tc=;
for(int k=; k<cp; k++)
{
if(xyd(crossProduct(p[i],p[i+],tp[k]),0.0))
s[tc++]=tp[k];
if(xy(crossProduct(p[i],p[i+],tp[k])*
crossProduct(p[i],p[i+],tp[k+]),0.0))
s[tc++]=IntersectPoint(p[i],p[i+],tp[k],tp[k+]);
}
s[tc]=s[];
for(int k=; k<=tc; k++)
tp[k]=s[k];
cp=tc;
}
len=cp;
} int main()
{
int t,n,m,i,j;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=; i<n; i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
}
//point tmp=IntersectPoint(p[0],p[1],p[2],p[3]);
//printf("%lf %lf\n",tmp.x,tmp.y);
Getsort(n);//for(i=0; i<n; i++)printf("%lf**%lf*\n",p[i].x,p[i].y);
int len;
cut(p,s,n,len);//for(i=0; i<len; i++)printf("%lf==%lf=\n",s[i].x,s[i].y);
double area=Area(s,len);
printf("%.2lf\n",area);
}
return ;
}
利用面积正负来判断顺or逆,这种代码是以逆时针为主,我的面积顺时针为正,
需要改变方向
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm> #define eps 1e-8
#define MAXX 1510 typedef struct point
{
double x;
double y;
}point; point p[MAXX],s[MAXX]; using namespace std;
bool dy(double x,double y)
{
return x>y+eps;
}
bool xy(double x,double y)
{
return x<y-eps;
}
bool dyd(double x,double y)
{
return x>y-eps;
}
bool xyd(double x,double y)
{
return x<y+eps;
}
bool dd(double x,double y)
{
return fabs(x-y)<eps;
} double crossProduct(point a,point b,point c)
{
return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x);
} point IntersectPoint(point u1,point u2,point v1,point v2)
{
point ans=u1;
double t = ((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x))/
((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));
ans.x += (u2.x-u1.x)*t;
ans.y += (u2.y-u1.y)*t;
return ans;
} double Area(point p[],int n)
{
double ans=0.0;
p[n]=p[];
point tmp;
tmp.x=,tmp.y=;
for(int i=; i<n; i++)
{
ans += crossProduct(tmp,p[i],p[i+]);
}
return ans/2.0;
} void changeWise(point p[],int n)
{
for(int i=; i<n/; i++)
swap(p[i],p[n-i-]);
} double dist(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
/*
bool cmp(point a,point b)
{
double tmp=crossProduct(p[0],a,b);
if(dd(tmp,0.0))
return dy(dist(p[0],a),dist(p[0],b));
return xy(tmp,0.0);
} point Getsort(int n)
{
int tmp=0;
for(int i=1; i<n; i++)
{
if(xy(p[i].x,p[tmp].x) || dd(p[i].x,p[tmp].x)&&xy(p[i].y,p[tmp].y))
{
tmp=i;
}
}// printf("%d^^",tmp);
swap(p[0],p[tmp]);
sort(p+1,p+n,cmp);
}
*/
void cut(point p[],point s[],int n,int &len)
{
point tp[MAXX];
p[n]=p[];
for(int i=; i<=n; i++)
{
tp[i]=p[i];
}
int cp=n,tc;
for(int i=; i<n; i++)
{
tc=;
for(int k=; k<cp; k++)
{
if(xyd(crossProduct(p[i],p[i+],tp[k]),0.0))
s[tc++]=tp[k];
if(xy(crossProduct(p[i],p[i+],tp[k])*
crossProduct(p[i],p[i+],tp[k+]),0.0))
s[tc++]=IntersectPoint(p[i],p[i+],tp[k],tp[k+]);
}
s[tc]=s[];
for(int k=; k<=tc; k++)
tp[k]=s[k];
cp=tc;
}
len=cp;
} int main()
{
int t,n,m,i,j;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=; i<n; i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
}
double tmp=Area(p,n);
if(dy(tmp,0.0))
changeWise(p,n);
//point tmp=IntersectPoint(p[0],p[1],p[2],p[3]);
//printf("%lf %lf\n",tmp.x,tmp.y);
//Getsort(n);for(i=0; i<n; i++)printf("%lf**%lf*\n",p[i].x,p[i].y);
int len;
cut(p,s,n,len);//for(i=0; i<len; i++)printf("%lf==%lf=\n",s[i].x,s[i].y);
double area=Area(s,len);
printf("%.2lf\n",fabs(area));
}
return ;
}
poj 1279 -- Art Gallery (半平面交)的更多相关文章
- POJ 1279 Art Gallery 半平面交/多边形求核
http://poj.org/problem?id=1279 顺时针给你一个多边形...求能看到所有点的面积...用半平面对所有边取交即可,模版题 这里的半平面交是O(n^2)的算法...比较逗比.. ...
- POJ 1279 Art Gallery 半平面交求多边形核
第一道半平面交,只会写N^2. 将每条边化作一个不等式,ax+by+c>0,所以要固定顺序,方便求解. 半平面交其实就是对一系列的不等式组进行求解可行解. 如果某点在直线右侧,说明那个点在区域内 ...
- POJ 1279 Art Gallery(半平面交)
题目链接 回忆了一下,半平面交,整理了一下模版. #include <cstdio> #include <cstring> #include <string> #i ...
- POJ 1279 Art Gallery 半平面交 多边形的核
题意:求多边形的核的面积 套模板即可 #include <iostream> #include <cstdio> #include <cmath> #define ...
- poj 1279 Art Gallery - 求多边形核的面积
/* poj 1279 Art Gallery - 求多边形核的面积 */ #include<stdio.h> #include<math.h> #include <al ...
- poj 1279 Art Gallery (Half Plane Intersection)
1279 -- Art Gallery 还是半平面交的问题,要求求出多边形中可以观察到多边形所有边的位置区域的面积.其实就是把每一条边看作有向直线然后套用半平面交.这题在输入的时候应该用多边形的有向面 ...
- POJ 1279 Art Gallery(半平面交求多边形核的面积)
题目链接 题意 : 求一个多边形的核的面积. 思路 : 半平面交求多边形的核,然后在求面积即可. #include <stdio.h> #include <string.h> ...
- [POJ]1279: Art Gallery
题目大意:有一个N边形展馆,问展馆内有多少地方可以看到所有墙壁.(N<=1500) 思路:模板题,半平面交求出多边形的核后计算核的面积. #include<cstdio> #incl ...
- POJ 1279 Art Gallery【半平面交】(求多边形的核)(模板题)
<题目链接> 题目大意: 按顺时针顺序给出一个N边形,求N边形的核的面积. (多边形的核:它是平面简单多边形的核是该多边形内部的一个点集该点集中任意一点与多边形边界上一点的连线都处于这个多 ...
随机推荐
- DirectX 绘制
先上图.后面会描写 ,细节
- tmpfs
什么是tmpfs tmpfs是Linux/Unix系统上的一种基于内存的文件系统.tmpfs可以使用您的内存或swap分区来存储文件.由此可见,temfs主要存储暂存的文件. linux内核中的VM子 ...
- 分享总结:更好地CodeReview
代码质量分享 2016_06_24_舒琴_代码质量.key For 代码提交人 基本原则 Review时机: 对于普通bugfix或优化,CodeReview最迟要 ...
- bootstrap实现 手机端滑动效果,滑动到下一页,jgestures.js插件
bootstrap能否实现 手机端滑动效果,滑动到下一页 jgestures.js插件可以解决,只需要引入一个JS文件<script src="js/jgestures.min.js& ...
- Servlet乱码
request.setCharacterEncoding():是设置从request中取得的值或从数据库中取出的值 (只管post方式提交的问题///get需在server.xml中的: < ...
- eclipse项目中启动项目无法载入类
在eclipse 项目中,当载入jar包后,加载里面的包,可以找到此类,但是编译运行的时候报错java.lang.ClassNotFoundException: 1,路径名未写正确: 2,配置出错; ...
- How to create UrlSlug in Asp.Net MVC
转自:http://www.ehsanghanbari.com/Post/20/how-to-create-urlslug-in-aspnet-mvc UrlSlug Is a way of gene ...
- Pro ASP.NET MVC 5 Framework.学习笔记.6.3.MVC的必备工具
每个MVC程序员的军火库中,都有这三个工具:一个依赖注入(DI)容器,一个单元测试框架,一个模拟工具. 1.准备一个示例项目 创建一个ASP.NET MVC Web Application的Empty ...
- 删除 SQL Server 2005 Express 工具
安装sql server 2008 management,提示错误:Sql2005SsmsExpressFacet 检查是否安装了 SQL Server 2005 Express 工具. 失败,已安装 ...
- Oracle存储过程返回游标实例详解
复制代码 代码如下:CREATE OR REPLACE PROCEDURE PROCSENDEMAIL(P_TXT VARCHAR2, P_SUB VARCHAR2, P_SENDOR VARCHAR ...
