POJ 1470 Closest Common Ancestors （LCA, dfs+ST在线算法）

Closest Common Ancestors

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 13370		Accepted: 4338

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form:

nr_of_vertices 
vertex:(nr_of_successors) successor1 successor2 ... successorn 
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form: 
nr_of_pairs 
(u v) (x y) ...

The input file contents several data sets (at least one). 
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times 
For example, for the following tree: 

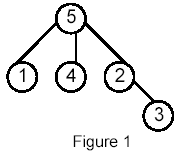
Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

Hint

Huge input, scanf is recommended.

Source

Southeastern Europe 2000

模板题

 /* ***********************************************
 Author        :kuangbin
 Created Time  :2013-9-5 8:54:16
 File Name     :F:\2013ACM练习\专题学习\LCA\POJ1470.cpp
 ************************************************ */

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <string>
 #include <math.h>
 #include <stdlib.h>
 #include <time.h>
 using namespace std;
 const int MAXN = ;
 int rmq[*MAXN];//rmq数组，就是欧拉序列对应的深度序列
 struct ST
 {
     int mm[*MAXN];
     int dp[*MAXN][];//最小值对应的下标
     void init(int n)
     {
         mm[] = -;
         for(int i = ;i <= n;i++)
         {
             mm[i] = ((i&(i-)) == )?mm[i-]+:mm[i-];
             dp[i][] = i;
         }
         for(int j = ; j <= mm[n];j++)
             for(int i = ; i + (<<j) -  <= n; i++)
                 dp[i][j] = rmq[dp[i][j-]] < rmq[dp[i+(<<(j-))][j-]]?dp[i][j-]:dp[i+(<<(j-))][j-];
     }
     int query(int a,int b)//查询[a,b]之间最小值的下标
     {
         if(a > b)swap(a,b);
         int k = mm[b-a+];
         return rmq[dp[a][k]] <= rmq[dp[b-(<<k)+][k]]?dp[a][k]:dp[b-(<<k)+][k];
     }
 };
 //边的结构体定义
 struct Edge
 {
     int to,next;
 };
 Edge edge[MAXN*];
 int tot,head[MAXN];

 int F[MAXN*];//欧拉序列，就是dfs遍历的顺序，长度为2*n-1,下标从1开始
 int P[MAXN];//P[i]表示点i在F中第一次出现的位置
 int cnt;

 ST st;
 void init()
 {
     tot = ;
     memset(head,-,sizeof(head));
 }
 void addedge(int u,int v)//加边，无向边需要加两次
 {
     edge[tot].to = v;
     edge[tot].next = head[u];
     head[u] = tot++;
 }
 void dfs(int u,int pre,int dep)
 {
     F[++cnt] = u;
     rmq[cnt] = dep;
     P[u] = cnt;
     for(int i = head[u];i != -;i = edge[i].next)
     {
         int v = edge[i].to;
         if(v == pre)continue;
         dfs(v,u,dep+);
         F[++cnt] = u;
         rmq[cnt] = dep;
     }
 }
 void LCA_init(int root,int node_num)//查询LCA前的初始化
 {
     cnt = ;
     dfs(root,root,);
     st.init(*node_num-);
 }
 int query_lca(int u,int v)//查询u,v的lca编号
 {
     return F[st.query(P[u],P[v])];
 }
 bool flag[MAXN];
 int Count_num[MAXN];
 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
     int n;
     int u,v,k;
     int Q;
     while(scanf("%d",&n) == )
     {
         init();
         memset(flag,false,sizeof(flag));
         for(int i = ;i <= n;i++)
         {
             scanf("%d:(%d)",&u,&k);
             while(k--)
             {
                 scanf("%d",&v);
                 flag[v] = true;
                 addedge(u,v);
                 addedge(v,u);
             }
         }
         int root;
         for(int i = ;i <= n;i++)
             if(!flag[i])
             {
                 root = i;
                 break;
             }
         LCA_init(root,n);
         memset(Count_num,,sizeof(Count_num));
         scanf("%d",&Q);
         while(Q--)
         {
             char ch;
             cin>>ch;
             scanf("%d %d)",&u,&v);
             Count_num[query_lca(u,v)]++;
         }
         for(int i = ;i <= n;i++)
             if(Count_num[i] > )
                 printf("%d:%d\n",i,Count_num[i]);
     }
     return ;
 }