混沌数学之CircuitChaotic(二维离散电路混沌系统)
相关软件参见:混沌数学之离散点集图形DEMO
相关代码:
// http://wenku.baidu.com/link?url=yg_gE7LUXCg2mXRp-ZZdfRXXIkcNj8YOhvN7dKLJxzWIu6M0g33-W3y3culjalCYfNc5VQefVJEiEwi_woXP69H8W4x-bF22nIRnD2lsn53
// 二维离散电路混沌系统
class CircuitChaotic : public DiscreteEquation
{
public:
CircuitChaotic()
{
m_StartX = 1.1832f;
m_StartY = 0.5916f; m_ParamA = 1.45f;
m_ParamB = 0.689f;
m_ParamC = 0.1f;
m_ParamD = 0.2f;
} void IterateValue(float x, float y, float& outX, float& outY) const
{
outX = m_ParamA*y - m_ParamD*y*y;
outY = -m_ParamB*x + m_ParamC*y;
} bool IsValidParamA() const {return true;}
bool IsValidParamB() const {return true;}
bool IsValidParamC() const {return true;}
bool IsValidParamD() const {return true;}
};
相关截图:


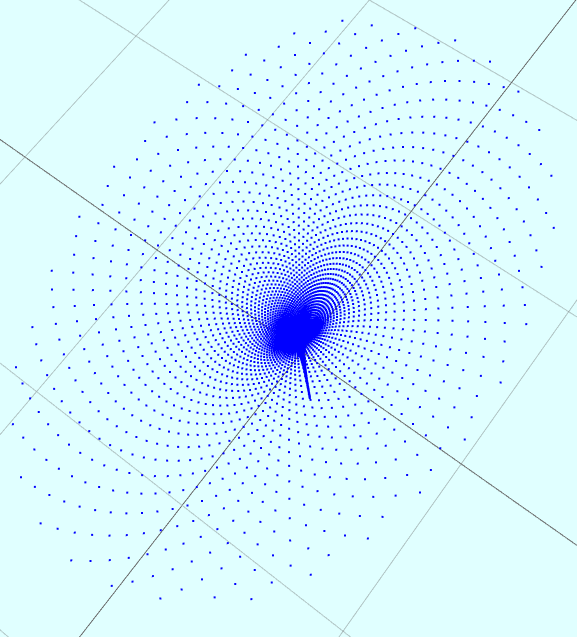

混沌数学之CircuitChaotic(二维离散电路混沌系统)的更多相关文章
- 多尺度二维离散小波重构waverec2
clc,clear all,close all; load woman; [c,s]=wavedec2(X,2,'haar');%进行2尺度二维离散小波分解.分解小波函数haar %多尺度二维离散小波 ...
- 单尺度二维离散小波重构(逆变换)idwt2
clc,clear all,close all; load woman; %单尺度二维离散小波分解.分解小波函数haar [cA,cH,cV,cD]=dwt2(X,'haar'); %单尺度二维离散小 ...
- 多尺度二维离散小波分解wavedec2
对X进行N尺度小波分解 [C,S]=wavedec2(X,N,'wname'); clc,clear all,close all; load woman; [c,s]=wavedec2(X,2,'db ...
- 单尺度二维离散小波分解dwt2
clc,clear all,close all; load woman; [cA,cH,cV,cD]=dwt2(X,'haar');%单尺度二维离散小波分解.分解小波函数haar figure,ims ...
- c语言数字图像处理(六):二维离散傅里叶变换
基础知识 复数表示 C = R + jI 极坐标:C = |C|(cosθ + jsinθ) 欧拉公式:C = |C|ejθ 有关更多的时域与复频域的知识可以学习复变函数与积分变换,本篇文章只给出DF ...
- 混沌数学之Chua's circuit(蔡氏电路)
蔡氏电路(英语:Chua's circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为.在1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者[1].这个电路的制作 ...
- Ios二维码扫描(系统自带的二维码扫描)
Ios二维码扫描 这里给大家介绍的时如何使用系统自带的二维码扫描方法和一些简单的动画! 操作步骤: 1).首先你需要搭建UI界面如图:下图我用了俩个imageview和一个label 2).你需要在你 ...
- 扫描二维码自动识别手机系统(Android/IOS)
移动互联网发展迅速,各种APP的开发都会推出多个版本(多终端),比如:iPhone版.iPad版.Android版.有些APP还会考虑覆盖到多个国家(国际化),比如:中文版.英文版.日文版.韩文版等. ...
- iOS二维码扫描IOS7系统实现
扫描相关类 二维码扫描需要获取摄像头并读取照片信息,因此我们需要导入系统的AVFoundation框架,创建视频会话.我们需要用到一下几个类: AVCaptureSession 会话对象.此类作为硬件 ...
随机推荐
- xmanager
[root@upright91 run]# ./runBenchmark.sh updbtpcc.properties sqlTableCreates Exception in thread &quo ...
- api设计 - php 接口 token 数据加密
最近在用php写app的接口,有一些疑问 首先关于token(令牌)token是用户登录的时候生成的 用户token在服务端保存入库 客户端则缓存在本地 大部分接口都要求客户端发送token 和服务端 ...
- Spark入门3(累加器和广播变量)
一.概要 通常情况下,当向Spark操作传递一个函数时,它会在一个远程集群节点上执行,它会使用函数中所有变量的副本.这些变量被复制到所有的机器上,远程机器上并没有被更新的变量会向驱动程序回传.在任务之 ...
- 洛谷P2525 Uim的情人节礼物·其之壱 [康托展开]
题目传送门 Uim的情人节礼物·其之壱 题目描述 情人节到了,Uim打算给他的后宫们准备情人节礼物.UIm一共有N(1<=N<=9)个后宫妹子(现充去死 挫骨扬灰!). 为了维护他的后宫的 ...
- [ 原创 ] Java基础3--Java中的接口
一.使用接口(interface)的目的 Java只支持单继承,即一个类最多只能继承一个直接父类,接口的主要功能就是可以实现类似于类的多重继承的功能. 二.接口的性质 1.接口具有继承性,即子接口可继 ...
- php 简单计算权重的方法(适合抽奖类的应用)
//简单权重计算器 $data222=array( 0=>array('id'=>1,'name'=>'一等奖','weight'=>'3'), 1=>a ...
- 【20181103T1】地球发动机【dp优化】
题面 一眼dp 设\(f_i\)表示前\(i\)个且\(i\)必须选的最大功率 有 \(f _i= max_{1 \leq j < i,A_i - A_j > X_j} \{f_j \}+ ...
- KMP 理解
例题 以字符串 ABABACA 为例 a 前缀: 后缀: 结果为0 ab 前缀:a 后缀: b 结果为0 aba 前缀:a ab 后缀: ba a 结果为1,此时 i=2,j=1 abab 前缀:a ...
- Alpha冲刺(1/10)——追光的人
1.队友信息 队员学号 队员博客 221600219 小墨 https://www.cnblogs.com/hengyumo/ 221600240 真·大能猫 https://www.cnblogs. ...
- SVN服务器与客户端下载地址_搭建使用
下载地址: http://subversion.apache.org/packages.html Windows CollabNet (supported and certified by Colla ...
