20162325 金立清 S2 W9 C18

20162325 2017-2018-2 《程序设计与数据结构》第9周学习总结

教材学习内容概要

---

堆是一棵完全二叉树，其中每个元素大于等于其所有子结点的值。
向堆中添加一个元素的方法是，首先将这个元素添加为叶结点，然后将其向上移动到合适的位置。
从堆中删除最大元素的方法是，首先将这个元素的叶结点来取代根，然后将其向下移动到合适的位置。
堆排序利用堆的基本特性对一组元素进行排序。
优先队列不是FIFO队列。它根据优先级排列元素，而不是根据它们进入队列的次序来排序。

堆

---

• 堆的定义如下：
  （1）堆是一颗完全二叉树；
  （2）堆树中某个节点的值总是不大于或不小于其孩子节点的值；
  （3）堆树中每个节点的子树都是堆树。
  当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。如下图所示，左边为最大堆，右边为最小堆。

• 辨析（以最大堆为例）：
  

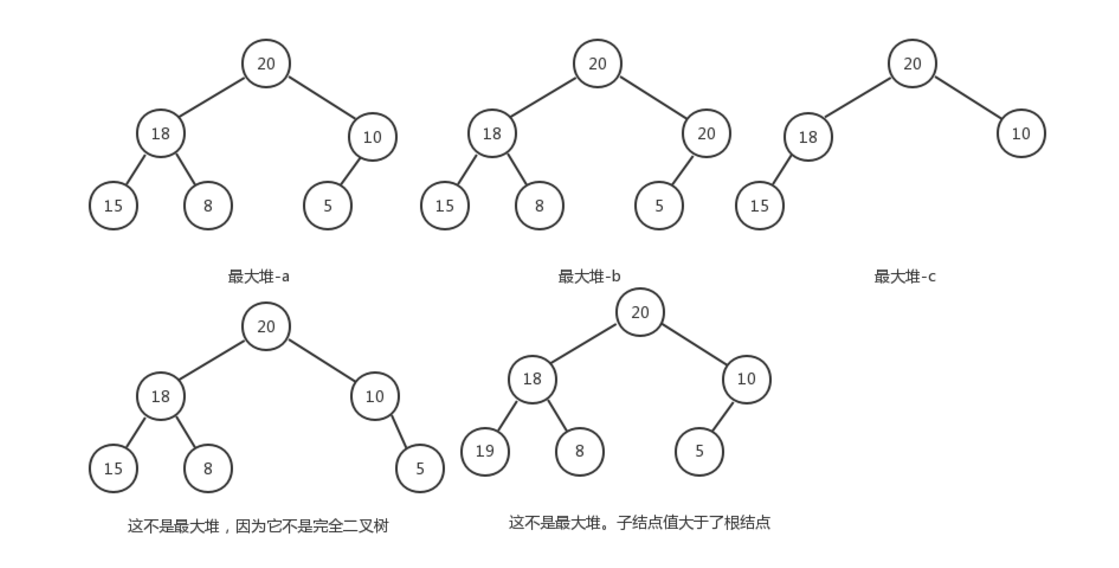
这里需要注意的是：在多个子树中，并不是说其中一个子树的父结点一定大于另一个子树的儿子结点。最大堆是树结构，而且一定要是完全二叉树。

备注：本章集中讨论最大堆，所有的操作通过翻转比较运算后都可适用于最小堆。如有需要可参考最小堆 构建、插入、删除的过程图解-CSDN博客理解。

向堆中添加一个元素

---

• 最大堆的插入操作可以简单看成是结点上浮。当我们在向堆中插入一个结点我们必须满足完全二叉树的标准，那么被插入结点的位置的是固定的。而且要满足父结点关键字值不小于子结点关键字值，那么我们就需要去移动父结点和子结点的相互位置关系。具体的位置变化，如下图：

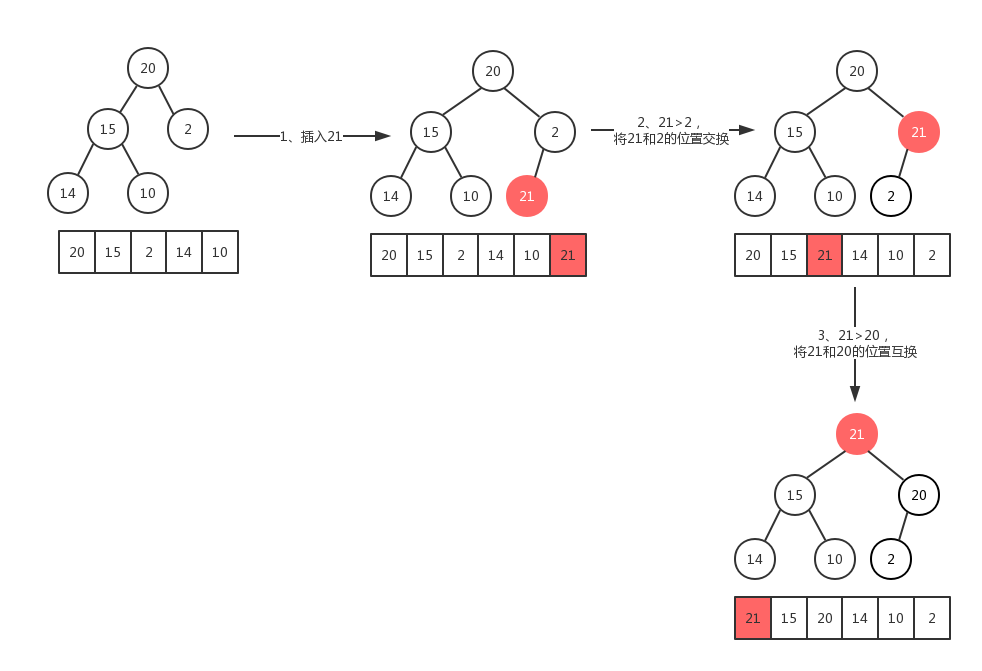
• 由于堆是一棵完全二叉树，存在n个元素，那么他的高度为:log2(n+1)，这就说明代码中的for循环会执行O(log2(n))次。因此插入函数的时间复杂度为：O(log2(n))。

从堆中删除最大元素

---

• 最大堆的删除操作，总是从堆的根结点删除元素。同样根元素被删除之后为了能够保证该树还是一个完全二叉树，我们需要来移动完全二叉树的最后一个结点，让其继续符合完全二叉树的定义，从这里可以看作是最大堆最后一个结点的下沉（也就是下文提到的结点1）操作。例如在下面的最大堆中执行删除操作：

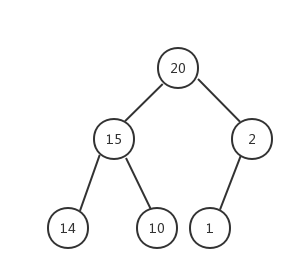
• 现在对上面