A Deep Neural Network’s Loss Surface Contains Every Low-dimensional Pattern

目录

• 概
• 相关工作
• 主要内容
  • 引理1
  • 定理1
  • 定理2

A Deep Neural Network’s Loss Surface Contains Every Low-dimensional Pattern

概

作者关于Loss Surface的情况做了一个理论分析, 即证明足够大的神经网络能够逼近所有的低维损失patterns.

相关工作

loss landscape 的提及.

文中多处用到了universal approximators.

主要内容

引理1

\(\mathcal{F}\)定义了universal approximators, 即同一定义域内的任意函数\(f\)都能用\(\mathcal{F}\)中的元素来逼近. \(\sigma(f_\theta)\)则是将值域进行了扩展, 而这并不影响其universal approximator的性质.

定理1

证明:

假设神经网络的第一层的权重矩阵为\(\theta_W \in \mathbb{R}^{d \times k}\), 偏置向量为\(\theta_b\), 神经网络剩余的参数为\(\theta'\), 记\(\theta = \{\theta_W, \theta_b, \theta'\}\). 则网络的输出为:

\[\tag{1}
f_{\theta}(x) = f_{\{\theta_W, \theta_b, \theta' \}}(x) = g_{\theta'}(\langle x, \theta_W \rangle + \theta_b),
\]

\(N\)个样本点的损失就是

\[\tag{2}
L(\theta) = \frac{1}{N} \sum_i \ell (f_{\theta}(x_i), y_i).
\]

现在假设目标\(z\)维loss pattern为(应当为连续函数)

\[\tag{3}
\mathcal{T}(h_1,h_2,\ldots, h_z):[0,1]^z \rightarrow [0, 1].
\]

我们现在, 希望将网络中的某些参数视作变量\(h_1,\ldots,h_z\), 得以逼近\(\mathcal{T}\).

令\(\theta_W=0\) (这样网络的输出与\(x\)无关), \(\theta_b=[h_1,\ldots, h_z,0,\ldots,0]\)(这隐含了\(k \ge z\)的假设).



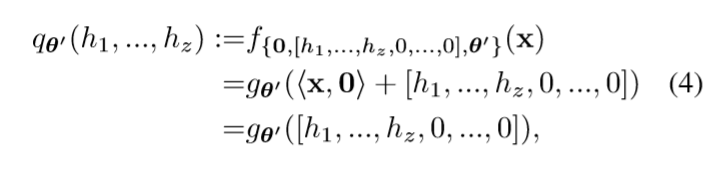
根据universal approximation theorem我们可以使得\(q_{\theta'}\)成为approximator. 相对应的

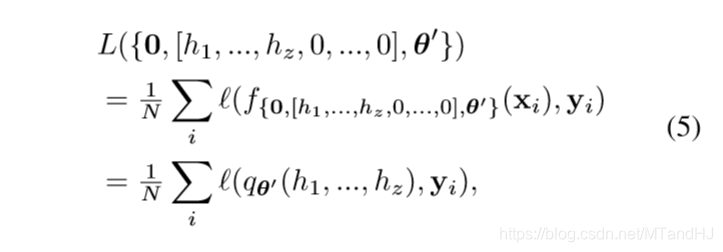
定义\(\sigma(p):=\frac{1}{N}\sum_i \ell(q_{\theta'}(h_1,\ldots, h_z),y_i)\), 只需要\(\sigma\)满足引理1中的条件, 就存在\(\theta_{\epsilon}(\mathcal{T})\), 使得\(L(h_1,h_2,\ldots, h_z, \theta_{\epsilon}(\mathcal{T}))\)逼近\(\mathcal{T}\).

定理2

说实话, 这个定理没怎么看懂, 看证明, 这个global minimum似乎指的是\(\mathcal{T}(h)\)的最小值.

证明:

\(\theta_b\)不变, \(\theta_W\)只令前\(z\)列为0, 则第一层(未经激活)的输出为\((h_1,\ldots,h_z，\phi(x))\), 于是

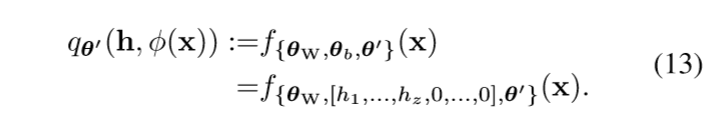
令\(h^* := \arg \min_{h \in [0,1]^z \mathcal{T}(h)}\), 并假设\(L^*=\mathcal{T}(h^*)\)(?). 假设损失\(\ell_i(p) = \ell (p, y_i)\), 可逆且逆函数光滑(这个性质对于损失函数来讲很普遍).

在这个假设下, 我们有

\[\tag{14}
q_{\theta'}(h, \phi(x_i)) \approx \ell_i^{-1}(\mathcal{T}(h)),
\]

文中说这个也是因为逼近定理, 固定\(i\)的时候, 这个自然是成立的, 如何能保证对于所有的\(i=1,\ldots,n\)成立, 我有一个思路.

假设二者的距离(\(+\infty\)范数)为\(\epsilon_i^h \in \mathbb{R}\), 则

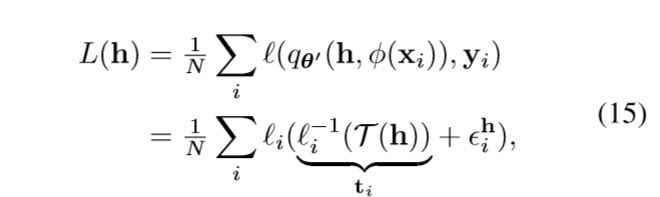
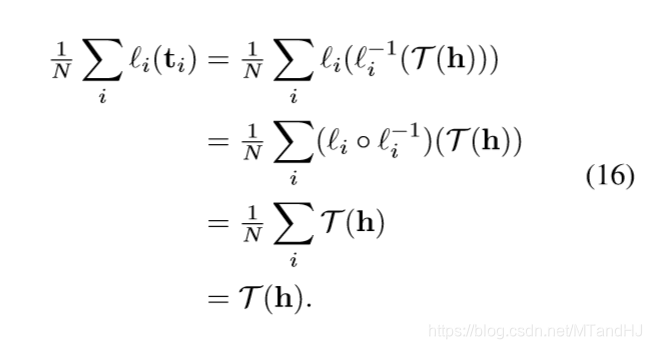
所以



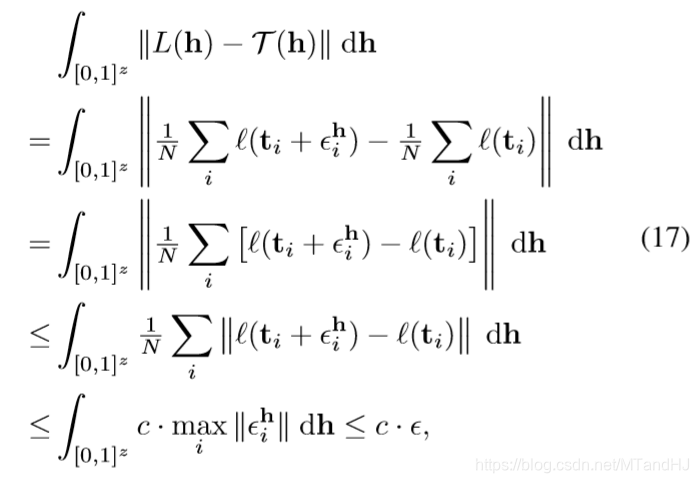
且此时\(|L(h^*)-\mathcal{T}(h^*)|<\epsilon\).

我比较关心的问题是, 能否选择合适的loss patterns (相当于选择合适的空间) 使得网络在某些性能上比较好(比方防过拟合, 最优性).