神经网络与机器学习 笔记—支持向量机（SVM）(上)

支持向量机（SVM）的主要思想：

给定训练样本，支持向量机建立一个超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化。

线性可分模式的最优超平面

训练样本{（xi,di）}^N i=1 ,其中xi是输入模式的第i个样例，di是对应的期望相应（目标输出）。首先假设由子集di=+1代表的模式（类）和di=-1代表的模式是“线性可分的”。用于分离的产平面形式的决策曲面方程是：

W^T X + b = 0

其中X是输入向量，W是可调的权值向量，b是偏置。因此可以写成:

W^T X + b  >= 0  当di=+1

W^T X + b   < 0  当di=-1

在这里做了模式线性可分的假设，以便在相当简单的环境里解释支持向量机背后的基本思想；对于一个给定的权值向量W和偏置b，由式W^T X + b = 0定义的超平面和最近的数据点之间的间隔被称为分离边缘，用ρ表示。支持向量机的目标是找到一个特殊的超平面，这个超平面的分离边缘ρ最大。在这种条件下，决策曲面称为最优超平面。

下面是二维空间中最优超平面的集合结构。

然后是进行处理和转化一下：

二维情况下点到最优超平面的袋鼠距离的几何解释：

满足

第一行或者第二行等号情况的特殊数据点（xi,di）称为支持向量，“支持向量机”因此得名。其他的训练样本完全不重要。由于支持向量的特点，这些向量在这类机器学习运行中起着主导作用。支持向量是最靠近决策面的数据点，这样的数据点是最难分类的。因此，他们和决策面的最优位置直接相关。同时各种推导之后会得到这么一个公式：

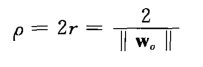
说明最大化两个类之间的分离边缘等价于最小化权值向量w的欧几里得范数。

最优超平面是唯一的，意味着最优权值向量w0提供正反例之间最大可能的分离。这个优化条件是通过最小化权值向量w的欧几里得范数获得的。

然后是基本上分四步类求这个超平面：

1. 寻找最优超平面问题，以这样一个陈述为开始：即在原始权重空间的带约束的优化问题。
2. 对于上述问题建立拉格朗日函数。[拉格朗日函数可以用来求目标函数约束条件下的极值]
3. 推到出极值最优化条件。
4. 问题的最后阶段是在对偶空间解决带拉格朗日乘子的优化问题。