【LeetCode】1462. 课程安排 IV Course Schedule IV (Python)

• 作者： 负雪明烛
• id： fuxuemingzhu
• 个人博客：http://fuxuemingzhu.cn/

---

目录

• 题目描述
• 题目大意
• 解题方法
• • DFS
• 日期

题目地址：https://leetcode-cn.com/problems/course-schedule-iv/

题目描述

你总共需要上 n 门课，课程编号依次为 0 到 n-1 。

有的课会有直接的先修课程，比如如果想上课程 0 ，你必须先上课程 1 ，那么会以 [1,0] 数对的形式给出先修课程数对。

给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。

对于每个查询对 queries[i] ，请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。

请返回一个布尔值列表，列表中每个元素依次分别对应 queries 每个查询对的判断结果。

注意：如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程，那么课程 a 也是课程 c 的先修课程。

示例 1：

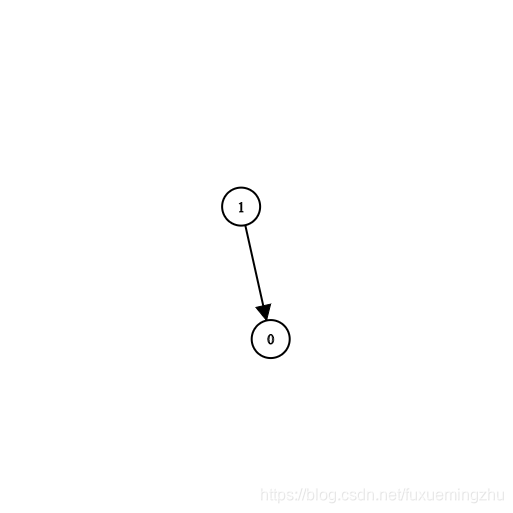
输入：n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

示例 2：

输入：n = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

示例 3：

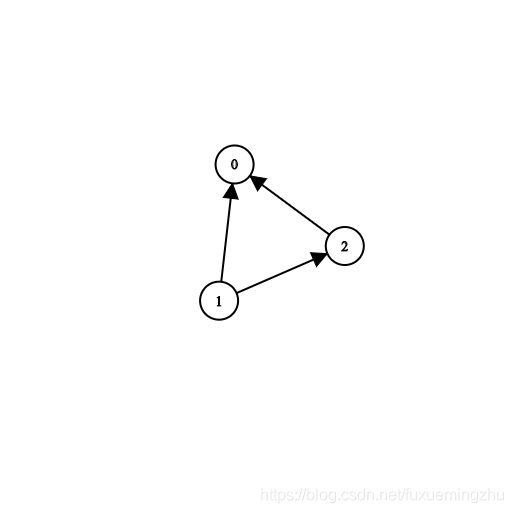
输入：n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

示例 4：

输入：n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
输出：[false,true]

示例 5：

输入：n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
输出：[true,false,true,false]

提示：

1. 2 <= n <= 100
2. 0 <= prerequisite.length <= (n * (n - 1) / 2)
3. 0 <= prerequisite[i][0], prerequisite[i][3] < n
4. prerequisite[i][0] != prerequisite[i][4]
5. 先修课程图中没有环。
6. 先修课程图中没有重复的边。
7. 1 <= queries.length <= 10^4
8. queries[i][0] != queries[i][5]

题目大意

题目给出了一个图。判断是否可以从queries[i][0]走向queries[i][1]。

解题方法

DFS

检查有向图中从queries[i][0]出发是否可以到达queries[i][1]，最简单的思路就是 DFS 看到能否搜索到。但是看了题目给出的数量级，估算如果每次query都在全图 DFS 搜索，时间复杂度为 O(queries.length * prerequisite.length) 约为 10^8 量级，则会超时。

那么 DFS 就不行了吗？并不见得。我们可以看出 DFS 会存在同一路径重复查找的现象，可以进行优化。

举例说明，假如题目给出的先修课程的图是这样的：

1 -> 2 -> 3 -> 4

假如第一个 query 判断了 1 -> 4 是可以的；
假如第二个 query 要判断 2 -> 4，是否需要重新搜索一遍呢？我们在第一个query中已经走过了这条路了呀，就没有必要重新搜索了。

即，我们的思路就是记录已经判断过的所有的路径，防止重复计算。比如在上面的例子中，我们在搜索 1 -> 4 的过程中，保存记录 1,2,3 都可以走到 4；如果下次再判断 2 是否能到 4 的时候，就可以在O(1)的时间内直接出结果了。

代码的实现时，先写出普通的 DFS 搜索是否可从 start 到达 end 的代码，然后可以用 Python3 提供的@functools.lru_cache，该函数能自动保存函数的参数和返回，相当于函数调用的记忆化。如果不用该函数，也可以自己定义memo数组来记录参数和返回。

• 时间复杂度：最好情况下只需要第一次搜索的时候把路径保存下来，之后查表就行，因此时间复杂度是 O(n)；最坏情况下，查询的时候从来没有走过重复的路径（比如星型的图），时间复杂度是O(N * queries.length)。
• 空间复杂度：最省空间的时候是没有保存过重复的路径，空间复杂度是O(1)；最费空间是把所有的节点两两路径保存，空间复杂度是O(N^2)。

Python 代码如下：

class Solution(object):
    def checkIfPrerequisite(self, n, prerequisites, queries):
        """
        :type n: int
        :type prerequisites: List[List[int]]
        :type queries: List[List[int]]
        :rtype: List[bool]
        """
        self.graph = collections.defaultdict(list)
        for pre in prerequisites:
            self.graph[pre[0]].append(pre[1])
        return [self.dfs(query[0], query[1]) for query in queries]

    # start -> end ?
    @functools.lru_cache
    def dfs(self, start, end):
        if start == end:
            return True
        return any(self.dfs(nxt, end) for nxt in self.graph[start])

欢迎关注负雪明烛的刷题博客，leetcode刷题800多，每道都讲解了详细写法！

日期

2020 年 6 月 1 日 —— 6月的开始，儿童节快乐！