linux文件属性和系统信息

文件属性

　　1.权限

　　　　权限指某一个用户针对某个文件所能做的操作

　　　　1.权限的种类

　　　　　　可读（r）

　　　　　　可写（w）

　　　　　　可执行（x）

　　　　　　无权限（-）

　　　　2.权限位

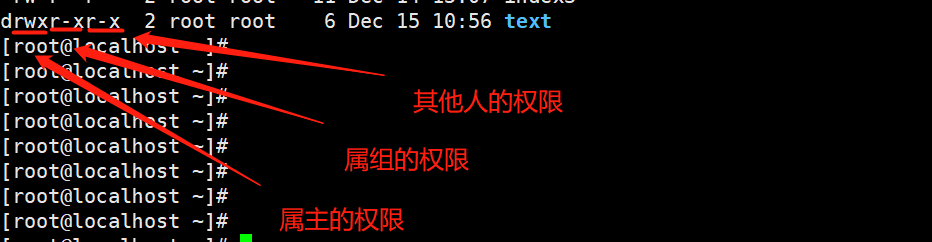
　　　　　　linux中的权限位分为三个部分，分别是属主、属组和其他人。

　　　　　　文件权限前三位表示属主，中间三位表示属组，后三位表示其他人。

　　　　3.数字编号

　　　　　　每一个权限都有一个数字编号。

　　　　　　　　可读(r) 　　　　　  　： 4
　　　　　　　　可写(w)　　　　　 　 ： 2
　　　　　　　　可执行(x) 　　　　      ： 1
　　　　　　　　没有对应权限（-）  　 ： 0

　　　　　　在添加权限的时候可以将权限加起来。

　　　　　　例如text的权限是属主rwx，属组r-x，其他人r-x

　　　　　　则等价于755（4+2+1,4+1,4+1）

　　　　4.添加权限

　　　　　　添加权限的命令为chmod，使用格式：

　　　　　　　　chmod [参数] [权限表达式] [操作对象]

　　　　　　参数：

　　　　　　　　-R：递归添加权限权限

　　　　5.权限的归属

　　　　　　属主：u

　　　　　　属组：g

　　　　　　其他人：o

　　　　　　可以用 角色 +/- 权限 的方式单独修改某个角色的权限

　　　　6.测试权限对于用户的意义

　　　　　　1.普通用户是要严格遵守权限的

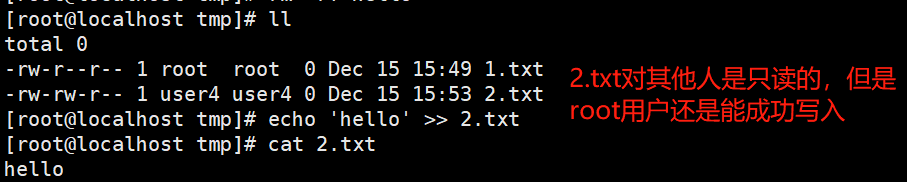
　　　　　　2.root用户是高于权限的

　　　　　　3.权限需要重新登录才生效

　　　　7.测试权限对于目录的意义

　　　　　　1.文件可读，路径的最小权限是必须有可执行权限

　　　　　　2.文件可写，路径的最小权限是必须有可执行权限

　　　　　　3.文件可执行，路径的最小权限是必须有可读和可执行权限

　　　　8.创建文件的默认权限

　　　　　　在linux中，常用文件的权限是666，目录的权限是777

　　　　　　1.文件的权限是跟umask值相减，遇到奇数加一，偶数不变。

　　　　　　2.文件夹的权限只要跟umask值相减即可。

　　　　

　　　　　　由此可见root用户以及组名和用户名不相同的用户，umask的值为022。

　　　　　　组名和用户名相同的普通用户，umask的值为002。

　　　　　　默认的文件权限：644

　　　　　　默认的文件夹权限是：755

　　2.文件时间信息

　　　　文件时间信息分为：

　　　　　　1.访问文件时间

　　　　　　2.修改文件时间

　　　　　　3.属性修改时间

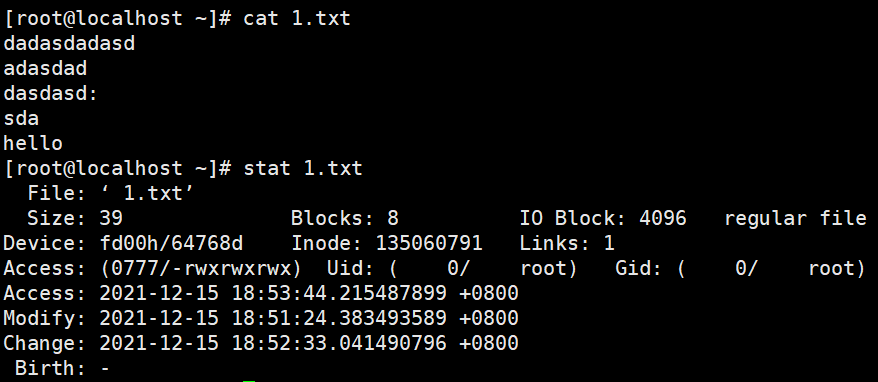
　　　　访问时间信息的命令：stat

　　　　时间信息变化情况：

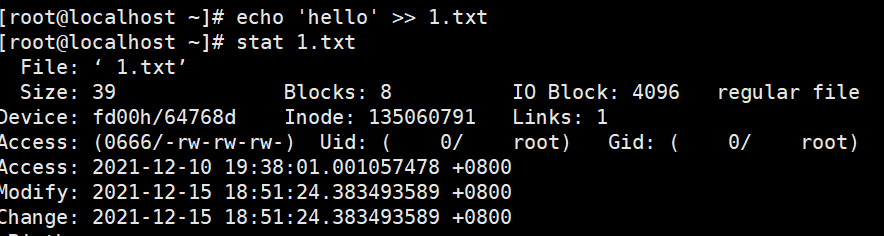
　　　　　　1.编辑文件内容

　　　　　　　　访问文件时间不变，修改时间改变，属性修改时间改变

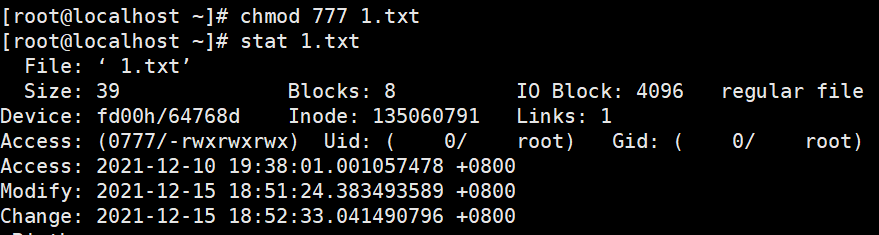
　　　　　　2.修改文件属性

　　　　　　　　访问文件时间不变，修改文件时间不变，属性修改时间改变

　　　　　　3.访问文件

　　　　　　　　访问文件时间改变，修改文件时间不变，属性修改时间不变

系统用户信息

　　1.系统用户信息

　　　　1.查看系统内核信息

　　　　　　命令：cat /etc/redhat-release

　　　　2.查看系统内核版本

　　　　　　

　　　　3.查看系统硬件位数

　　2.设置用户密码

　　　　1.交互方式

　　　　　　passwd [用户名]

　　　　2.非交互方式

　　　　　　echo [密码]|passwd --stdin [用户名]

　　3.命令提示信息

　　　　1.临时修改方式

　　　　　　export PS1=‘[\u@\h \W]\$’（W表示路径最后一位，w表示全部路径）

　　　　2.永久修改方式

　　　　　　修改/etc/profile文件，在其中添加export PS1='[\u@\h \w]\$'

　　搭建yum私有仓库

　　　　1.创建目录充当仓库

　　　　2.下载软件，存放于yum仓库中

　　　　　　1.安装wget

　　　　　　2.在yumrepo文件下创建Packages目录

　　　　　　3.下载软件到Packages目录

　　　　3.建立依赖关系

　　　　　　1.下载建立依赖关系的命令

　　　　　　2.建立yum源的依赖关系

　　　　4.编写yum源

　　　　　　1.来到/etc/yum.repos.d下将原有的源放到别的目录

　　　　　　2.创建新的源文件

　　　　　　3.编写repo文件

　　　　　　　　　   名称

　　　　　　　　　　简介

　　　　　　　　　　地址

　　　　　　　　　　安全验证

　　　　　　4.更新源

　　　　　　　　

　　　　5.测试