【Matlab】线性调频信号LFM 仿真
【知识点】
生成序列
i = a:step:b
举例:
i = 1:1:9

画图(子图)
subplot(m,n,p)或者subplot(m n p)
总结起来就是,画一个m行n列的图。
p表示在第p个位置。
subplot是将多个图画到一个平面上的工具。其中,m表示是图排成m行,n表示图排成n列,也就是整个figure中有n个图是排成一行的,一共m行,如果m=2就是表示2行图。p表示图所在的位置,p=1表示从左到右从上到下的第一个位置。(横着数)时间序列的间隔
间隔时间\(T_s=\frac{1}{F_s}\)
(这里我要再看一下dsp)
B = 70e6; %带宽70MHzT = 2e-6; %脉宽2usFs = 100e6; %采样率N = T*Fs; %采样点数t = -T/2:1/Fs:T/2-1/Fs; %时间序列K = B/T; %线性调频率St = exp(j*pi*K*t.^2); %信号theta = pi*K*t.^2; %相位f = K*t; %信号频率%画图figuresubplot(2,2,1);plot(real(St));title('信号实部');subplot(2,2,2);plot(imag(St));title('信号虚部');subplot(2,2,3);plot(theta);title('信号相位');subplot(2,2,4);plot(f);title('信号频率 Hz');%figure2%plot(abs(fftshift(fft(St))));title('信号频谱');
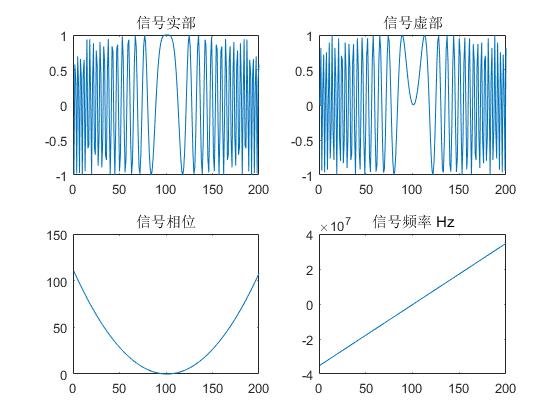
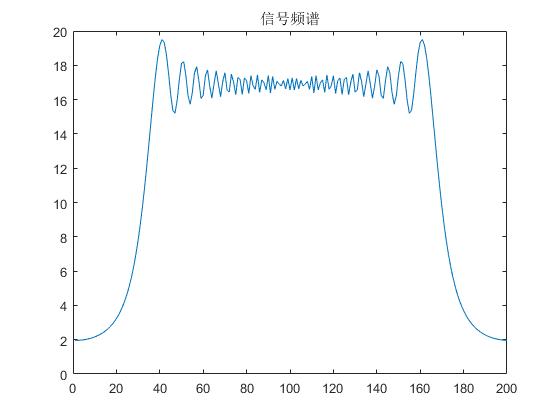
【Matlab】线性调频信号LFM 仿真的更多相关文章
- 信号基础知识----线性调频信号LFM //matlab命令:chirp
%关于线性调频信号(LFM) %参考书目:声呐技术,第二章P33 clc;close all;clear all;%参数----------------------------------f0=100 ...
- 用MATLAB对信号做频谱分析
1.首先学习下傅里叶变换的东西.学高数的时候老师只是将傅里叶变换简单的说了下,并没有深入的讲解.而现在看来,傅里叶变换似乎是信号处理的方面的重点只是呢,现在就先学习学习傅里叶变换吧. 上面这幅图在知乎 ...
- MATLAB与Carsim联合仿真时提示matlab not found的解决方法(CarSim在联合仿真时提示找不到MATLAB的解决方法)
CarSim8.02并没有提供选择联合仿真的MATLAB/Simulink的版本的功能,CarSim总是与最后安装的MATLAB/Simulink进行联合仿真,如果安装有多个matlab版本则只打开最 ...
- MATLAB处理信号得到频谱、相谱、功率谱
(此帖引至网络资源,仅供参考学习)第一:频谱 一.调用方法 X=FFT(x):X=FFT(x,N):x=IFFT(X);x=IFFT(X,N) 用MATLAB进行谱分析时注意: (1)函数FFT返回值 ...
- 震荡信号Simulink仿真
1. simulink仿真设计 震荡信号本质是调制信号,可以表示为: u(t)=A*(1+m*cos(Ωt+θ))*cos(ωt+φ)=A*cos (ωt+φ)+ A*m*cos(Ωt+θ)*cos( ...
- 利用Matlab实现PID控制仿真
该文转自博客园: https://www.cnblogs.com/kui-sdu/p/9048534.html %PID Controller clear, clc, close all; ts=0. ...
- Matlab/Modelsim图像联合仿真平台
FPGA图像仿真平台 1 引言 在使用modelsim进行图像算法的功能仿真时,无法得到图像的实时预览,因此直观性有所欠缺.因此可配合matlab使用,通过modelsim读出txt格式的图像,利用m ...
- matlab数据导入verilog仿真
Matlab中的fopen和fprintf函数可以生成txt格式文件,并将波形数据以 %d 整数 %e 实数:科学计算法形式 %f 实数:小数形式 %g 由系统自动选取上述两种格式之一 %s 输出字符 ...
- matlab 正弦信号产生
fs=2400;%设定采样频率N=1000; %采样的点数n=0:N-1;t=n/fs; %1/fs相当于隔多长时间才一个点f1=50;%设定争先信号频率xn=sin(2*pi*f1*t);figur ...
随机推荐
- scrapy的安装,scrapy创建项目
简要: scrapy的安装 # 1)pip install scrapy -i https://pypi.douban.com/simple(国内源) 一步到位 # 2) 报错1: building ...
- 基于ambari搭建hadoop生态圈大数据组件
Ambari介绍1Apache Ambari是一种基于Web的工具,支持Apache Hadoop集群的供应.管理和监控.Ambari已支持大多数Hadoop组件,包括HDFS.MapReduce.H ...
- 行星万象表白墙微信小程序、社交微信小程序,后台完整,支持多区域运营,扫码体验。
简介 中国目前大概有5000个表白墙,累计用户近3000万,是一个庞大的群体,但现在大都以微信朋友圈为基础进行信息中转,但是这种模式经营者和用户都不友好,尤其是经营者无法变现,用户无法公开评论,这些种 ...
- [atARC096F]Sweet Alchemy
给定一棵有根树,记$f_{i}$表示$i$的父亲,每一个点有一个代价$c_{i}$ 给定常数$D$和$X$,再给每个点赋一个权值$v_{i}$($v_{i}\ge 0$),满足以下条件下最大化$\su ...
- 应用SpringAOP及Tlog工具完成日志链路追踪、收集、持久化
一.痛点 目前我司各系统的日志管理比较原始,使用logback打日志到log文件,虽然有服务管理平台,但记录的日志也仅仅是前置机调用后台系统的出入参,当遇到问题时查日志较为麻烦. 登录VPN-打开服务 ...
- [Net 6 AspNetCore Bug] 解决返回IAsyncEnumerable<T>类型时抛出的OperationCanceledException会被AspNetCore 框架吞掉的Bug
记录一个我认为是Net6 Aspnetcore 框架的一个Bug Bug描述 在 Net6 的apsnecore项目中, 如果我们(满足以下所有条件) api的返回类型是IAsyncEnumerabl ...
- mybatis-批量操作数据(list对象 )
在实际工作中老是忘记 传入的参数和数据库参数名称要一致还是与实体类型一致导致很多笑话发生. 那我还是做个记录吧! dao层: int addRemark(@Param("list" ...
- Redis | 第5章 Redis 中的持久化技术《Redis设计与实现》
目录 前言 1. RDB 持久化 1.1 RDB 文件的创建与载入 1.2 自动间隔性保存 1.2.1 设置保存条件 1.2.2 dirty 计数器和 lastsave 属性 1.2.3 检查保存条件 ...
- java番外茶余饭后闲聊
java番外茶余饭后闲聊 **本人博客网站 **IT小神 www.itxiaoshen.com 今天聊点题外话没事时可以作为平时沟通交流的谈资,接下来一起简单了解下个人知晓对Java界开发产生深远影响 ...
- RNA_seq 热图绘制
若已经拿到表达矩阵exprSet 若差异较大,进行log缩小不同样本的差距 1.热图全体 1 ##加载包 2 library(pheatmap) 3 4 ##缩小表达量差距 5 exprSet < ...
