HDU2363 最短路+贪心

Cycling

Time Limit: 5000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1418    Accepted Submission(s): 467

Problem Description

You want to cycle to a programming contest. The shortest route to the contest might be over the tops of some mountains and through some valleys. From past experience you know that you perform badly in programming contests after experiencing large differences in altitude. Therefore you decide to take the route that minimizes the altitude difference, where the altitude difference of a route is the difference between the maximum and the minimum height on the route. Your job is to write a program that finds this route.
You are given:

the number of crossings and their altitudes, and

the roads by which these crossings are connected.
Your program must find the route that minimizes the altitude difference between the highest and the lowest point on the route. If there are multiple possibilities, choose the shortest one.
For example:

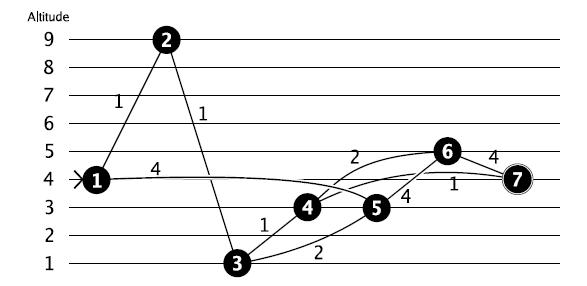
In this case the shortest path from 1 to 7 would be through 2, 3 and 4, but the altitude difference of that path is 8. So, you prefer to go through 5, 6 and 4 for an altitude difference of 2. (Note that going from 6 directly to 7 directly would have the same difference in altitude, but the path would be longer!)

 

Input

On the first line an integer t (1 <= t <= 100): the number of test cases. Then for each test case:

One line with two integers n (1 <= n <= 100) and m (0 <= m <= 5000): the number of crossings and the number of roads. The crossings are numbered 1..n.

n lines with one integer hi (0 <= h_i <= 1 000 000 000): the altitude of the i-th crossing.

m lines with three integers a_j , b_j (1 <= a_j , b_j <= n) and c_j (1 <= c_j <= 1 000 000): this indicates that there is a two-way road between crossings a_j and b_j of length c_j . You may assume that the altitude on a road between two crossings changes linearly.
You start at crossing 1 and the contest is at crossing n. It is guaranteed that it is possible to reach the programming contest from your home.

 

Output

For each testcase, output one line with two integers separated by a single space:

the minimum altitude difference, and

the length of shortest path with this altitude difference.

 

Sample Input

1

7 9

4 9 1 3
3
5
4

1 2 1

2 3 1

3 4 1

4 7 1

1 5 4

5 6 4

6 7 4

5 3 2

6 4 2

 

Sample Output

2 11

 

Source

bapc2007_pre

 题意：

n个点，m条路，每个点有一个权值，求从1点出发到n点，经过的点的权值最大与最小之差最小的一条最短路。

代码：

//这题气炸了，用dijk怎么做怎么不对，改了spfa才过的。要求最小差值的最短路可以把所有的点之间的差值
//算出来，按照差值从小到大排序，从小到大枚举每一个差值所对应的高度上下界，在这个范围之内求
//最短路，求到的第一个就是结果。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<vector>
using namespace std;
const int inf=0x7fffffff;
int dis[],vis[],hig[];
int up,low,t,n,m,cnt;
struct Lu
{
    int x,y,w;
}L[];
bool cmp(Lu x,Lu y) {return x.w<y.w;}
struct node{
    int to,value;
};
vector<node>g[];
int spfa()
{
    int s=;
    for(int i=;i<=n;i++)
        dis[i]=inf;
    memset(vis,,sizeof(vis));
    vis[s]=;
    dis[s]=;
    queue<int>q;
    q.push(s);
    while(!q.empty()){
        int cur=q.front();
        q.pop();
        vis[cur]=;
        if(hig[cur]<low||hig[cur]>up) continue; //起始点也不例外
        for(int i=;i<(int)g[cur].size();i++){
            int k=g[cur][i].to;
            if(hig[k]<low||hig[k]>up) continue;  //在范围之中
            if(dis[k]>dis[cur]+g[cur][i].value){
                dis[k]=dis[cur]+g[cur][i].value;
                if(!vis[k]){
                    vis[k]=;
                    q.push(k);
                }
            }
        }
    }
    return dis[n];
}
int main()
{
    int x,y,z,ans1,ans2;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        cnt=;ans2=inf;
        for(int i=;i<=n;i++){
            g[i].clear();     //记住。
            scanf("%d",&hig[i]);
        }
        for(int i=;i<=n;i++){
            for(int j=i;j<=n;j++){  //有可能起点等于终点所以j从i开始
                L[cnt].x=min(hig[i],hig[j]);
                L[cnt].y=max(hig[i],hig[j]);
                L[cnt].w=L[cnt].y-L[cnt].x;
                cnt++;
            }
        }
        for(int i=;i<=m;i++){
            scanf("%d%d%d",&x,&y,&z);
            node no;
            no.to=y;
            no.value=z;
            g[x].push_back(no);
            no.to=x;
            g[y].push_back(no);
        }
        sort(L,L+cnt,cmp);
        int flag=,tmp;
        for(int i=;i<cnt;i++){
            if(flag&&tmp<L[i].w) break;//出现高度差一样，最短路不同的情况
            low=L[i].x;up=L[i].y;
            int ans=spfa();
            if(ans!=inf){
                ans1=L[i].w;
                ans2=min(ans2,ans);
                flag=;
                tmp=L[i].w;
            }
        }
        printf("%d %d\n",ans1,ans2);
    }
    return ;
}