BZOJ3028 食物 和 LOJ6261 一个人的高三楼

总结一下广义二项式定理。

食物

明明这次又要出去旅游了，和上次不同的是，他这次要去宇宙探险！我们暂且不讨论他有多么NC，他又幻想了他应该带一些什么东西。理所当然的，你当然要帮他计算携带N件物品的方案数。他这次又准备带一些受欢迎的食物，如：蜜桃多啦，鸡块啦，承德汉堡等等当然，他又有一些稀奇古怪的限制，每种食物的限制如下：

1. 承德汉堡：偶数个
2. 可乐：0个或1个
3. 鸡腿：0个，1个或2个
4. 蜜桃多：奇数个
5. 鸡块：4的倍数个
6. 包子：0个，1个，2个或3个
7. 土豆片炒肉：不超过一个。
8. 面包：3的倍数个

注意，这里我们懒得考虑明明对于带的食物该怎么搭配着吃，也认为每种食物都是以‘个’为单位（反正是幻想嘛），只要总数加起来是N就算一种方案。因此，对于给出的N,你需要计算出方案数，并对10007取模。

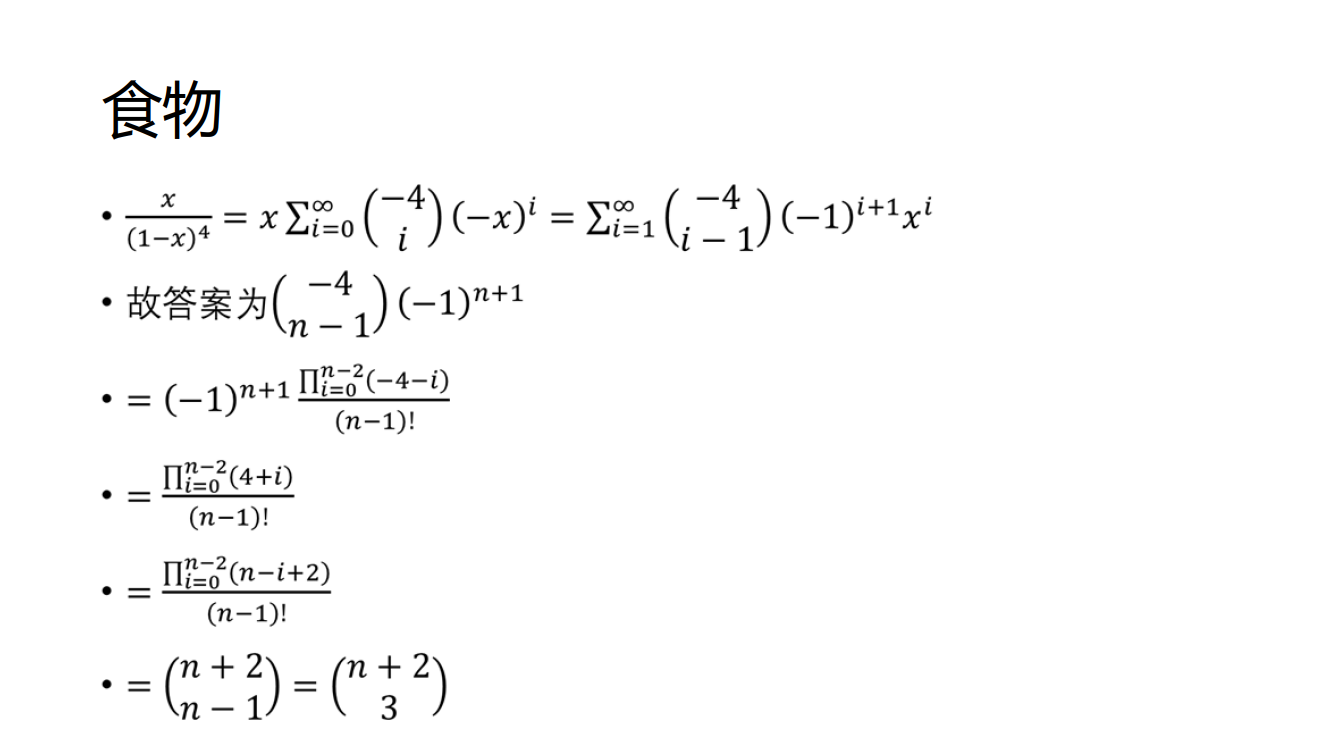
co int mod=10007;
int main(){
	int n=0;char c=getchar();
	while(!isdigit(c)) c=getchar();
	for(;isdigit(c);c=getchar()) n=(n*10+c-'0')%mod;
	n=(n+2)%mod;
	printf("%lld\n",(LL)n*(n-1)*(n-2)/6%mod);
	return 0;
}

一个人的高三楼

给你一个长度为n的数列a_i，求它的k次前缀和模998244353。（就是做k次前缀和后的数列）

n≤10⁵,k≤2⁶⁰。

zsy的题解

设\(F_t(x)\)表示数列在做过\(t\)次前缀和之后的生成函数。

尝试构造一个函数\(G(x)\)，满足\(F_t(x)G(x)\equiv F_{t+1}(x) \mod x^n\)。

发现\(G(x)=\sum_{i=0}^{n}x^i\)。

所以有\(F_k(x)=F_0(x)G^k(x)\)。直接多项式快速幂即可，理论复杂度\(O(n\log n)\)。

考虑一下上式的组合意义。因为\(G(x)\)的每一项都是1，那么\([x^i]G^k(x)\)相当于从\(k\)个盒子里取出若干个球使取出来的总数为\(i\)方案数。在这里认为盒子不同而球相同。而这个方案数显然是可以组合算的，用隔板法即可。

也就是说，\(G^k(x)=\sum_{i=0}^{n}\binom{i+k-1}{k-1}x^i\)。

发现\(k\)非常大不好预处理组合数。考虑组合数的一个同层的递推式：\(\binom{n+1}{m}=\binom{n}{m}\times\frac{n+1}{n-m+1}\)。

所以直接递推即可，复杂度\(O(n\log n)\)。

co int N=4e5;
int a[N],b[N];
int rev[N],omg[N];

void num_trans(int a[],int lim){
	for(int i=0;i<lim;++i)if(i<rev[i]) swap(a[i],a[rev[i]]);
	for(int i=1;i<lim;i<<=1)
		for(int j=0;j<lim;j+=i<<1)
			for(int k=0;k<i;++k){
				int t=mul(omg[lim/(i<<1)*k],a[j+i+k]);
				a[j+i+k]=add(a[j+k],mod-t),a[j+k]=add(a[j+k],t);
			}
}
int main(){
	int n=read<int>(),K=read<LL>()%mod;
	for(int i=1;i<=n;++i) read(a[i]);
	b[0]=1;
	for(int i=1;i<=n;++i) b[i]=mul(b[i-1],mul(i+K-1,fpow(i,mod-2)));

	int len=ceil(log2(2*n+1)),lim=1<<len;
	for(int i=0;i<lim;++i) rev[i]=rev[i>>1]>>1|(i&1)<<(len-1);
	omg[0]=1,omg[1]=fpow(3,(mod-1)/lim);
	for(int i=2;i<lim;++i) omg[i]=mul(omg[i-1],omg[1]);
	num_trans(a,lim),num_trans(b,lim);
	for(int i=0;i<lim;++i) a[i]=mul(a[i],b[i]);
	omg[1]=fpow(omg[1],mod-2);
	for(int i=2;i<lim;++i) omg[i]=mul(omg[i-1],omg[1]);
	num_trans(a,lim);
	int ilim=fpow(lim,mod-2);
	for(int i=1;i<=n;++i) printf("%d\n",mul(a[i],ilim));
	return 0;
}

LOJ又炸了。代码回归简洁了。