DP问题(3) : hdu 1080

题目转自hdu 1080，题目传送门

---

题目大意：

不想翻译！

---

解题思路：

其实就是一道变异的求lcs（Longest common subsequence 最长公共子序列）的题

不过，它的依据是下面这张图：

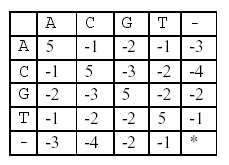
所以，需要一个数组来存规则：

int ta[][]={
    {,-,-,-,-},
    {-,,-,-,-},
    {-,-,,-,-},
    {-,-,-,,-},
    {-,-,-,-,}
};

同时，需要把每个字母对应成一个数字

处理字母对应代码如下：

int get_init(char s)
{
    if(s=='A') return ;
    else if(s=='C') return ;
    else if(s=='G') return ;
    else if(s=='T') return ;
    else return ;
}

但有是由于它的计分标准要按照那个表计算

所以我们要通过函数来计算所对应的分值：

int get_value(char s1,char s2)
{
    int x=get_init(s1);
    int y=get_init(s2);
    return ta[x][y];
}

但是，令人头秃的是如何初始化......

于是，思考了0.5h后，我放弃了

后来，我去问了lhc学长（学长博客点此，被迫推荐）

然后这位大佬看了题，没过10min就读懂了

1min后，初始化代码就被他写出来了，如下：

for(int i=;i<=l1;i++) dp[i][]=dp[i-][]+get_value(s1[i],'-');
for(int i=;i<=l2;i++) dp[][i]=dp[][i-]+get_value('-',s2[i]);

p.s.这代码我可看了0.25h才看懂，大佬真的很nb

然后随便写一个n²的dp就可以愉快地AC了......（愉快吗？）

---

AC代码如下：

#include<iostream>
#include<stdio.h>
#include<string.h>
#define maxn 105
using namespace std;
char s;
char s1[maxn],s2[maxn];
int T,l1,l2;
int dp[maxn][maxn];
int ta[][]={
    {,-,-,-,-},
    {-,,-,-,-},
    {-,-,,-,-},
    {-,-,-,,-},
    {-,-,-,-,}
};
int get_init(char s)
{
    if(s=='A') return ;
    else if(s=='C') return ;
    else if(s=='G') return ;
    else if(s=='T') return ;
    else return ;
}
int get_value(char s1,char s2)
{
    int x=get_init(s1);
    int y=get_init(s2);
    return ta[x][y];
}
void dp_lcs(int l1,int l2)
{
    for(int i=;i<=l1;i++)
        for(int j=;j<=l2;j++)
            dp[i][j]=max(dp[i-][j-]+get_value(s1[i],s2[j]),max(dp[i-][j]+get_value(s1[i],'-'),dp[i][j-]+get_value('-',s2[j])));
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        memset(dp,,sizeof(dp));
        scanf("%d%s",&l1,s1+);
        scanf("%d%s",&l2,s2+);
        dp[][]=;
        for(int i=;i<=l1;i++) dp[i][]=dp[i-][]+get_value(s1[i],'-');
        for(int i=;i<=l2;i++) dp[][i]=dp[][i-]+get_value('-',s2[i]);
        dp_lcs(l1,l2);
        printf("%d\n",dp[l1][l2]);
    }
    return ;
}

码风清奇，不喜勿喷

从这道题我们可以看出，有几个大佬当朋友还是有用的......