【CSP模拟赛】starway（玄学建边 最小生成树）

问題描述

小w伤心的走上了 Star way to heaven。
   到天堂的道路是一个笛卡尔坐标系上一个n×m的长方形通道(顶点在(0,0)）和（n,m))，小w从最左边任意一点进入，从右边任意一点走到天堂。
   最左最右的距离为n，上下边界距离为m。
   其中长方形内有k个Star，每个Star都有一个整点坐标，Star的大小可以忽略不计，
   每个Star以及长方形上下两个边缘（宇宙的边界）都有引力，所以为了成功到达heaven小w离他们越远越好。
   请问小V走到终点的路径上，距离所有星星以及边界的最小距离最大值可以为多少？

输入格式

一行三个整数n,m,k。
   接下来k行，每行两个整数x_i,y_i表示一个点的坐标。

输出格式

一行一个整数表示答案，绝对误差不能超过10^-6。
输入样例
    10 5 2
    1 1
    2 3
输出样例
    1.11803399
    对于100%的数据 $k\leq 6000 ,n,m\leq 10^6$

分析

没什么好分析的，noi.ac上的原题都不会做了，可见这个Oier有多菜

根据套路，题目中说到最小距离最大，我们考虑二分这个最小距离然后检验

设最小距离为len

对于一个点，如果到它的最小距离为len，那么以它为圆心，len为半径形成的圆就是雷区，是不能进入的

对于一条线，雷区就是一个贼长的矩形

下图是len为1时样例的雷区

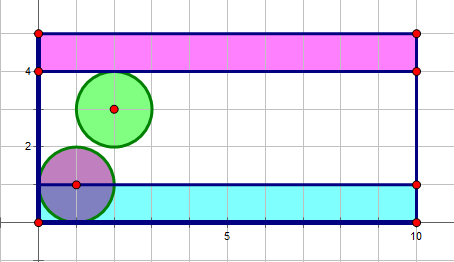
显然，如果小w只走白色区域就可以从左边走到右边，那么这个len就是可以在增加一些的

那么如何判断这些雷区可以封死小w走的路呢？

我们来看一下封死的情况，让len为$\sqrt 2$

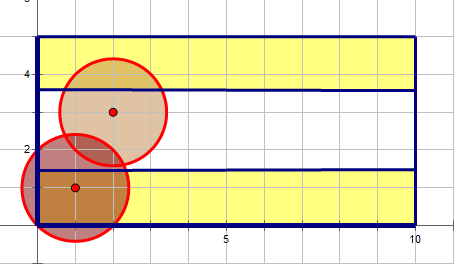
如果把上下边界也看成点，距离小于len*2的点连边

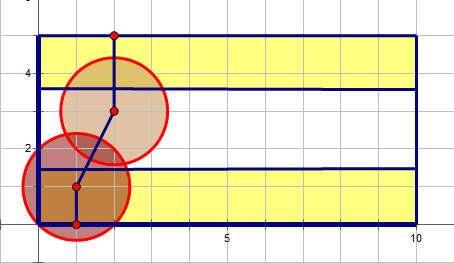
我们发现，若是上下两个边界联通了，就从左边到右边的路就被封死了。

于是我们可以二分len然后O(n^2)连边，O(n)判定，复杂度为O(nlogn)

不过6000的数据还是过不了。

由联通，所以想到最小生成树，在最小生成树中，从下边界到上边界路径上最长的边应该就是限制上下边界联通的边，拿它除以2就是答案

然而身为年度憨憨人物的我忘了prim只记得kruskal，暴力最小生成树

prim的时间复杂度为O(n^2),kruskal的时间复杂度为O(mlogm),此题m=n^2

所以选择prim算法。

如果怕精度问题可以用longlong存下距离的平方

#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,k,vis[],pre[],p[][];long long d[],ans;
long long dis(int a,int b){return 1ll*(p[a][]-p[b][])*(p[a][]-p[b][])+1ll*(p[a][]-p[b][])*(p[a][]-p[b][]);}
int main()
{
    scanf("%d%d%d",&n,&m,&k);d[k+]=1ll*m*m;
    for(int i=;i<=k;i++)scanf("%d%d",&p[i][],&p[i][]),d[i]=1ll*p[i][]*p[i][];
    for(int i=;i<=k+;i++)
    {
        int nx=;long long mn=1000000000000ll;
        for(int j=;j<=k+;j++)if(d[j]<=mn&&!vis[j])mn=d[nx=j];
        if(nx==k+){d[nx]=ans=mn;break;}vis[nx]=;
        for(int j=;j<=k+;j++)
        if(j==k+)
            pre[j]=d[j]>1ll*(m-p[nx][])*(m-p[nx][])?nx:pre[j],
            d[j]=min(d[j],1ll*(m-p[nx][])*(m-p[nx][]));
        else if(!vis[j]&&d[j]>dis(j,nx))d[j]=dis(j,nx),pre[j]=nx;
    }
    int x=k+;while(x)ans=max(ans,d[x]),x=pre[x];
    printf("%.9lf\n",sqrt(ans)/2.0);
}