QuantLib 金融计算——收益率曲线之构建曲线（4）

如果未做特别说明，文中的程序都是 C++11 代码。

QuantLib 金融计算——收益率曲线之构建曲线（4）

本文代码对应的 QuantLib 版本是 1.15。相关源代码可以在 QuantLibEx 找到。

概述

QuantLib 中提供了用三次 B 样条函数拟合期限结构的功能，但是，并未提供使用三次样条函数拟合期限结构的功能。本文展示了如何在 QuantLib 的框架内实现三次样条函数，并拟合期限结构。

示例所用的样本券交易数据来自专门进行期限结构分析的 R 包——termstrc。具体来说是数据集 govbonds 中的 GERMANY 部分，包含 2008-01-30 这一天德国市场上 52 只固息债的成交数据。

注意：为了适配 QuantLib，实际计算中删除了两只债券的数据，以保证所有样本券的到期时间均不相同。样本券数据在《收益率曲线之构建曲线（3）》的附录中列出。

三次样条函数与期限结构

用三次样条函数拟合期限结构，实质上是用若干三次样条函数的组合近似贴现因子曲线的形状，

\[d(t,\beta) = 1 + \sum_{l=1}^n \beta_l c_l(t)
\]

贴现因子 \(d(t,\beta)\) 表示为三次样条函数的线性组合，\(\beta_l\) 是最优化计算需要估计出的参数。

三次样条函数 \(c_l(t)\) 的形式基于文献 (Ferstl and Hayden, 2010)，

\[\begin{cases}
& \text{ if } l=n, c_l(t)=t\\
& \text{ else }, c_{l}\left(t\right)=
\left\{\begin{array}{ll}
0 & {t<k_{l-1}} \\
{\frac{\left(t-k_{l-1}\right)^{3}}{6\left(k_{l}-k_{l-1}\right)}} & {k_{l-1} \leq t<k_{l}} \\
{\frac{\left(k_{l}-k_{l-1}\right)^{2}}{6}+\frac{\left(k_{l}-k_{l-1}\right)\left(t-k_{l}\right)}{2}+\frac{(t-k_l)^2}{2} -\frac{\left(t-k_{l}\right)^{3}}{6\left(k_{l+1}-k_{l}\right)}} & {k_{l} \leq t<k_{l+1}} \\
{\left(k_{l+1}-k_{l-1}\right)\left[\frac{2 k_{l+1}-k_{l}-k_{l-1}}{6}+\frac{t-k_{l+1}}{2}\right]} & {k_{l+1} \leq t}
\end{array}\right.
\end{cases}
\]

对于有 \(n\) 个参数的贴现因子曲线，用户需要提供 \(n-1\) 个 knots \(k_i(1\le i\lt n)\)，并令 \(k_0 = 0\) 以及 \(k_n = k_{n-1}\)。

knots 的选择

knots 的选择基于文献 (McCulloch, 1975)，也可以参考文献 (Ferstl and Hayden, 2010)，

\[\begin{cases}
& \text{ if } l=1, k_l = 0\\
& \text{ else if } l=n-1,k_l=m_N \\
& \text{ else }, k_l = m_h + \theta(m_{h+1} - m_h)
\end{cases}
\]

其中，\(h=\left\lceil\frac{(l-1) k}{n-2}\right\rceil\)，\(\theta=\frac{(l-1) k}{n-2}-h\)，\(n = \left\lfloor\sqrt{k}+0.5 \right\rfloor\)，\(m_i(1 \le i\le N)\) 是升序排列后样本券的剩余期限。

实现三次样条函数

三次样条函数类 CubicSpline 的实现仿照已存在的 BSpline 类，

CubicSpline.hpp

class CubicSpline {

  public:

    CubicSpline(const std::vector<Real>& knots);

    ~CubicSpline();

    Real operator()(Natural i, Real x) const;

  private:

    Size n_;

    std::vector<Real> knots_ex_;

};

CubicSpline.cpp

CubicSpline::CubicSpline(const std::vector<Real>& knots)

    : n_(knots.size() + 1), knots_ex_(knots) {

    knots_ex_.insert(knots_ex_.begin(), 0.0);

    knots_ex_.insert(knots_ex_.end(), knots.back());

}

CubicSpline::~CubicSpline() {

}

Real CubicSpline::operator()(Natural i, Real x) const {

    using namespace std;

    if (i < n_) {

        Real q = knots_ex_[i], q_minus = knots_ex_[i - 1], q_plus = knots_ex_[i + 1];

        if (x < q_minus) {

            return 0.0;

        } else if (q_minus <= x and x < q) {

            return pow(x - q_minus, 3) / (6.0 * (q - q_minus));

        } else if (q <= x and x < q_plus) {

            return pow(q - q_minus, 2) / 6.0

                   + (q - q_minus) * (x - q) / 2.0

                   + pow(x - q, 2) / 2.0

                   - pow(x - q, 3) / (6.0 * (q_plus - q));

        } else {

            return (q_plus - q_minus)

                   * ((2.0 * q_plus - q - q_minus) / 6.0

                      + (x - q_plus) / 2.0);

        }

    } else {

        return x;

    }

}

实现拟合方法

拟合方法 CubicSplinesFitting 的实现仿照已存在的 CubicBSplinesFitting 类，两者均是 FittedBondDiscountCurve::FittingMethod 的派生类，

CubicSplinesFitting.hpp

class CubicSplinesFitting

    : public FittedBondDiscountCurve::FittingMethod {

  public:

    CubicSplinesFitting(const std::vector<Time>& knotVector,

                        const Array& weights = Array(),

                        ext::shared_ptr<OptimizationMethod>

                            optimizationMethod = ext::shared_ptr<OptimizationMethod>(),

                        const Array& l2 = Array());

    CubicSplinesFitting(const std::vector<Time>& knotVector,

                        const Array& weights,

                        const Array& l2);

    //! cubic spline basis functions

    Real basisFunction(Integer i, Time t) const;

    static std::vector<Time> autoKnots(const std::vector<Time>& maturities);

#if defined(QL_USE_STD_UNIQUE_PTR)

    std::unique_ptr<FittedBondDiscountCurve::FittingMethod> clone() const;

#else

    std::auto_ptr<FittedBondDiscountCurve::FittingMethod> clone() const;

#endif

  private:

    Size size() const;

    DiscountFactor discountFunction(const Array& x, Time t) const;

    CubicSpline splines_;

    Size size_;

    //! N_th basis function coefficient to solve for when d(0)=1

    Natural N_;

};

CubicSplinesFitting.cpp

CubicSplinesFitting::CubicSplinesFitting(const std::vector<Time>& knots,

                                         const Array& weights,

                                         ext::shared_ptr<OptimizationMethod> optimizationMethod,

                                         const Array& l2)

    : FittedBondDiscountCurve::FittingMethod(

          false, weights, optimizationMethod, l2),

      splines_(knots) {

    Size basisFunctions = knots.size() + 1;

    size_ = basisFunctions;

    N_ = 0;

}

CubicSplinesFitting::CubicSplinesFitting(const std::vector<Time>& knots,

                                         const Array& weights,

                                         const Array& l2)

    : FittedBondDiscountCurve::FittingMethod(

          false, weights, ext::shared_ptr<OptimizationMethod>(), l2),

      splines_(knots) {

    Size basisFunctions = knots.size() + 1;

    size_ = basisFunctions;

    N_ = 0;

}

Real CubicSplinesFitting::basisFunction(Integer i,

                                        Time t) const {

    return splines_(i, t);

}

QL_UNIQUE_OR_AUTO_PTR<FittedBondDiscountCurve::FittingMethod> CubicSplinesFitting::clone() const {

    return QL_UNIQUE_OR_AUTO_PTR<FittedBondDiscountCurve::FittingMethod>(

        new CubicSplinesFitting(*this));

}

Size CubicSplinesFitting::size() const {

    return size_;

}

DiscountFactor CubicSplinesFitting::discountFunction(const Array& x,

                                                     Time t) const {

    DiscountFactor d = 1.0;

    for (Size i = 0; i < size_; ++i) {

        d += x[i] * splines_(i + 1, t);

    }

    return d;

}

std::vector<Time> CubicSplinesFitting::autoKnots(const std::vector<Time>& maturities) {

    using namespace std;

    vector<Time> m(maturities);

    sort(m.begin(), m.end());

    Size k = m.size();

    Size n(floor(sqrt(k) + 0.5));

    vector<Time> knots(n - 1);

    knots[0] = 0.0;

    knots[n - 1] = m.back();

    for (Size l = 1; l < n - 1; ++l) {

        Size h(ceil(Real(l * k) / Real(n - 2)));

        Real theta = Real(l * k) / Real(n - 2) - h;

        knots[l] = m[h - 1] + theta * (m[h] - m[h - 1]);

    }

    return knots;

}

测试

用上述两个类拟合样本券的期限结构，并和 termstrc 的结果做比较。

辅助函数 CubicSplineSpotRate 用于将样条函数表示的贴现因子转换成即期利率。

QuantLib::Real CubicSplineSpotRate(const std::vector<QuantLib::Real>& knots,

                                   const QuantLib::Array& weights,

                                   const QuantLib::Time& t) {

    using namespace std;

    using namespace QuantLib;

    CubicSpline spline(knots);

    Size s = weights.size();

    Real d = 1.0, r;

    for (Size i = 0; i < s; ++i) {

        d += weights[i] * spline(i + 1, t);

    }

    r = -std::log(d) / t;

    return r;

}

测试函数

void TestCubicSplineFitting() {

    using namespace std;

    using namespace QuantLib;

    // 样本券数据，以及相关配置

    Size bondNum = 50;

    vector<Real> cleanPrice = {

        100.002, 99.92, 99.805, 99.75, 100.305, 99.76, 99.75, 99.975, 100.0416, 100.0574,

        99.5049, 101.0971, 101.137, 100.7199, 99.8883, 100.908, 103.3553, 99.5034, 103.913, 97.4229,

        104.5636, 99.7527, 104.3708, 99.6051, 104.8603, 101.3415, 105.29, 102.4969, 103.7602, 100.2803,

        102.6046, 102.5291, 99.4748, 95.9702, 97.1815, 114.2849, 100.2847, 112.23, 98.397, 102.0235,

        99.8483, 121.2711, 125.9157, 114.5791, 103.2202, 123.4668, 113.4694, 103.1873, 91.5603, 95.4441};

    vector<Handle<Quote>> priceHandle(bondNum);

    for (Size i = 0; i < bondNum; ++i) {

        ext::shared_ptr<Quote> q(

            new SimpleQuote(cleanPrice[i]));

        Handle<Quote> hq(q);

        priceHandle[i] = hq;

    }

    vector<Year> issueYear = {

        2002, 2006, 2003, 2006, 1998, 2006, 2003, 2006, 1999, 2007,

        2004, 2007, 1999, 2007, 2004, 2007, 1999, 2005, 2000, 2005,

        2000, 2006, 2001, 2006, 2001, 2007, 2002, 2007, 2002, 2003,

        2003, 2004, 2004, 2005, 2005, 1986, 2006, 1986, 2006, 2007,

        2007, 1993, 1997, 1998, 1998, 2000, 2000, 2003, 2004, 2006};

    vector<Month> issueMonth = {

        Aug, Mar, Apr, May, Jul, Aug, Sep, Nov, Jan, Feb,

        Feb, May, Jul, Aug, Aug, Sep, Oct, Feb, May, Aug,

        Sep, Feb, May, Aug, Dec, Feb, Jun, Aug, Dec, Jun,

        Oct, Apr, Oct, Apr, Oct, Jun, Apr, Sep, Oct, Apr,

        Sep, Dec, Jul, Jan, Oct, Jan, Oct, Jan, Dec, Dec};

    vector<Day> issueDay = {

        14, 8, 11, 30, 4, 30, 25, 30, 4, 28, 2, 30, 4, 24, 25, 21, 22,

        24, 5, 26, 29, 26, 23, 30, 28, 28, 26, 24, 31, 24, 21, 25, 27, 28,

        30, 20, 26, 20, 31, 27, 21, 29, 3, 4, 7, 4, 27, 22, 24, 28};

    vector<Year> maturityYear = {

        2008, 2008, 2008, 2008, 2008, 2008, 2008, 2008, 2009, 2009,

        2009, 2009, 2009, 2009, 2009, 2009, 2010, 2010, 2010, 2010,

        2011, 2011, 2011, 2011, 2012, 2012, 2012, 2012, 2013, 2013,

        2014, 2014, 2015, 2015, 2016, 2016, 2016, 2016, 2017, 2017,

        2018, 2024, 2027, 2028, 2028, 2030, 2031, 2034, 2037, 2039};

    vector<Month> maturityMonth = {

        Feb, Mar, Apr, Jun, Jul, Sep, Oct, Dec, Jan, Mar,

        Apr, Jun, Jul, Sep, Oct, Dec, Jan, Apr, Jul, Oct,

        Jan, Apr, Jul, Oct, Jan, Apr, Jul, Oct, Jan, Jul,

        Jan, Jul, Jan, Jul, Jan, Jun, Jul, Sep, Jan, Jul,

        Jan, Jan, Jul, Jan, Jul, Jan, Jan, Jul, Jan, Jul};

    vector<Day> maturityDay = {

        15, 14, 11, 13, 4, 12, 10, 12, 4, 13, 17, 12, 4, 11, 9, 11,

        4, 9, 4, 8, 4, 8, 4, 14, 4, 13, 4, 12, 4, 4, 4, 4, 4, 4, 4,

        20, 4, 20, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4};

    vector<Date> issueDate(bondNum), maturityDate(bondNum);

    for (Size i = 0; i < bondNum; ++i) {

        Date idate(issueDay[i], issueMonth[i], issueYear[i]);

        Date mdate(maturityDay[i], maturityMonth[i], maturityYear[i]);

        issueDate[i] = idate;

        maturityDate[i] = mdate;

    }

    vector<Real> couponRate = {

        0.0425, 0.03, 0.03, 0.0325, 0.0475, 0.035, 0.035, 0.0375, 0.0375, 0.0375,

        0.0325, 0.045, 0.045, 0.04, 0.035, 0.04, 0.05375, 0.0325, 0.0525, 0.025,

        0.0525, 0.035, 0.05, 0.035, 0.05, 0.04, 0.05, 0.0425, 0.045, 0.0375, 0.0425,

        0.0425, 0.0375, 0.0325, 0.035, 0.06, 0.04, 0.05625, 0.0375, 0.0425, 0.04,

        0.0625, 0.065, 0.05625, 0.0475, 0.0625, 0.055, 0.0475, 0.04, 0.0425};

    Frequency frequency = Annual;

    Actual365Fixed dayCounter(Actual365Fixed::Standard);

    BusinessDayConvention paymentConv = Unadjusted;

    BusinessDayConvention terminationDateConv = Unadjusted;

    BusinessDayConvention convention = Unadjusted;

    Real redemption = 100.0;

    Real faceAmount = 100.0;

    Germany calendar(Germany::Eurex);

    Date today = calendar.adjust(Date(30, Jan, 2008));

    Settings::instance().evaluationDate() = today;

    Natural bondSettlementDays = 0;

    Date bondSettlementDate = calendar.advance(

        today,

        Period(bondSettlementDays, Days));

    vector<ext::shared_ptr<BondHelper>> instruments(bondNum);

    vector<Time> maturity(bondNum);

    // 配置 helper

    for (Size i = 0; i < bondNum; ++i) {

        vector<Real> bondCoupon = {couponRate[i]};

        Schedule schedule(

            issueDate[i],

            maturityDate[i],

            Period(frequency),

            calendar,

            convention,

            terminationDateConv,

            DateGeneration::Backward,

            false);

        ext::shared_ptr<FixedRateBondHelper> helper(

            new FixedRateBondHelper(

                priceHandle[i],

                bondSettlementDays,

                faceAmount,

                schedule,

                bondCoupon,

                dayCounter,

                paymentConv,

                redemption));

        maturity[i] = dayCounter.yearFraction(

            bondSettlementDate, helper->maturityDate());

        instruments[i] = helper;

    }

    Real tolerance = 1.0e-6;

    Natural max = 5000;

    ext::shared_ptr<OptimizationMethod> optMethod(

        new LevenbergMarquardt());

    vector<Real> knots = CubicSplinesFitting::autoKnots(maturity);

    vector<Real> termstrcKnotes = {

        0.000000, 1.006027, 2.380274, 5.033425, 9.234521, 31.446575};

    cout << "QuantLib knots:\t";

    for (auto v : knots) {

        cout << setprecision(6) << fixed << v << ", ";

    }

    cout << endl;

    cout << "termstrc knots:\t";

    for (auto v : termstrcKnotes) {

        cout << setprecision(6) << fixed << v << ", ";

    }

    cout << endl;

    cout << endl;

    CubicSplinesFitting csf(

        knots, Array(), optMethod);

    FittedBondDiscountCurve tsCubicSplines(

        bondSettlementDate,

        instruments, dayCounter,

        csf, tolerance, max);

    Array weights = tsCubicSplines.fitResults().solution();

    Array termstrcWeights(7);

    termstrcWeights[0] = 1.9320e-02, termstrcWeights[1] = -8.4936e-05,

    termstrcWeights[2] = -3.2009e-04, termstrcWeights[3] = -3.7101e-04,

    termstrcWeights[4] = 7.2921e-04, termstrcWeights[5] = 2.0159e-03,

    termstrcWeights[6] = -4.1632e-02;

    cout << "QuantLib weights: \t" << weights << endl;

    cout << "termstrc weights: \t" << termstrcWeights << endl;

    cout << endl;

    cout << "QuantLib final cost value:\t"

         << tsCubicSplines.fitResults().minimumCostValue() << endl;

    cout << endl;

    // 比较 QuantLib 和 termstrc 的结果

    Real spotRate, termstrcSpot;

    for (Size i = 0; i < bondNum; ++i) {

        Time t = dayCounter.yearFraction(

            bondSettlementDate, maturityDate[i]);

        spotRate =

            tsCubicSplines.zeroRate(t, Compounding::Continuous, frequency).rate() * 100.0;

        termstrcSpot =

            CubicSplineSpotRate(termstrcKnotes, termstrcWeights, t) * 100.0;

        cout << setprecision(3) << fixed

             << t << ",\t"

             << spotRate << ",\t"

             << termstrcSpot << ",\t"

             << spotRate - termstrcSpot << endl;

    }

}

部分结果：

QuantLib knots:	0.000000, 1.117808, 2.690411, 5.430137, 9.432877, 31.446575,

termstrc knots:	0.000000, 1.006027, 2.380274, 5.033425, 9.234521, 31.446575,

QuantLib weights: 	[ 0.005281; 0.004565; -0.002934; 0.000804; 0.000652; 0.001886; -0.038316 ]

termstrc weights: 	[ 0.019320; -0.000085; -0.000320; -0.000371; 0.000729; 0.002016; -0.041632 ]

QuantLib final cost value:	0.000338

0.044,	3.823,	4.125,	-0.302

0.121,	3.809,	4.061,	-0.253

0.197,	3.794,	4.001,	-0.207

0.370,	3.761,	3.878,	-0.116

...

..

.

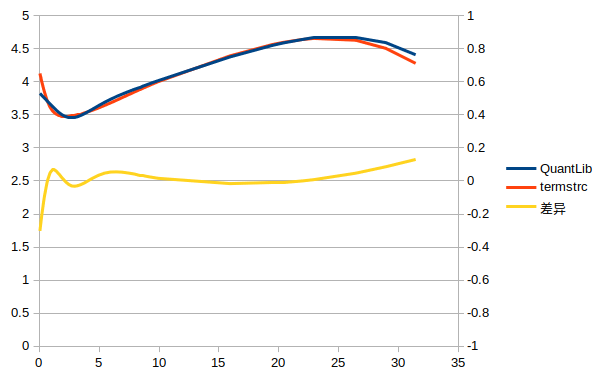
图 1：结果对比

注意：尽管以 termstrc 的结果作为基准，并不意味着基准就是正确答案。

由于样本券的数量不同（termstrc 使用了 52 只券），两者的 knots 差异较大。同时，因为优化方法的不同（termstrc 使用 OLS，QuantLib 使用 Levenberg-Marquardt 算法），估计出的参数也有差异。最终导致两个期限结构在两端差异较大。

不过，考虑到最终的 cost value，QuantLib 的结果可能更好一些。

参考文献

Ferstl.R, Hayden.J (2010). "Zero-Coupon Yield Curve Estimation with the Package termstrc." Journal of Statistical Software, Volume 36, Issue 1.
McCulloch JH (1975). "The Tax-Adjusted Yield Curve." The Journal of Finance, 30(3), 811–830.