LDA算法 (主题模型算法) 学习笔记
转载请注明出处: http://www.cnblogs.com/gufeiyang
随着互联网的发展,文本分析越来越受到重视。由于文本格式的复杂性,人们往往很难直接利用文本进行分析。因此一些将文本数值化的方法就出现了。LDA就是其中一种很NB的方法。 LDA有着很完美的理论支撑,而且有着维度小等一系列优点。本文对LDA算法进行介绍,欢迎批评指正。
本文目录:
1、Gamma函数
2、Dirichlet分布
3、LDA文本建模
4、吉普斯抽样概率公式推导
5、使用LDA
1、Gamma函数
T(x)= ∫ tx-1 e-tdt T(x+1) = xT(x)
若x为整数,则有 T(n) = (n-1)!
2、Dirichlet分布
这里抛出两个问题:
问题1: (1) X1, X2......Xn 服从Uniform(0,1)
(2) 排序后的顺序统计量为X(1), X(2), X(3)......X(n)
(3) 问X(k1)和X(k1+k2)的联合分布式什么
把整个概率区间分成[0,X1) , [X1, X1+Δ), [X1+Δ, X1+X2), [X1+X2, X1+X2+Δ), [X1+X2+Δ,1]
X(k1) 在区间[X1, X1+Δ), X(k1+k2) 在区间[X1+X2, X1+X2+Δ)。 我们另X3 = 1-X1-X2.
则,
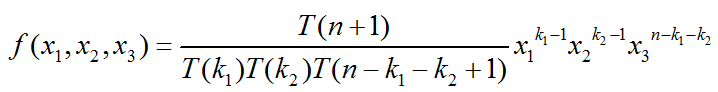
即Dir(x1, x2, x3| k1, k2, n-k1-k2+1)
问题2: (1) X1, X2......Xn 服从Uniform(0,1), 排序后的顺序统计量为X(1), X(2), X(3)......X(n)
(2) 令p1 = [0, X(k1)], p2 = [X(k1), X(k1+k2)], p3 = 1-p1-p2
(3) 另外给出新的信息, Y1, Y2.....Ym服从Uniform(0, 1), Yi落到[0,X(k1)], [X(k1), X(k1+k2)], [X(k1+k2), 1]的数目分别是m1, m2, m3
(4) 问后验概率 p(p1,p2,p3|Y1,Y2,....Ym)的分布。
其实这个问题和问题1很像,只是在同样的范围内多了一些点而已。 因此这个概率分布为 Dir(x1,x2,x3| k1+m1, k2+m2, n-k1-k2+1+m3)。
我们发现这么一个规律 Dir(p|k) + multCount(m) = Dir(p|k+m)。 即狄利克雷分布是多项分布的共轭分布。
狄利克雷分布有这么一个性质:如果 则,
则,

3、 LDA文本建模
首先我们想一篇文章是如何形成的:作者在写一篇文章的时候首先会想这个文章需要包含什么主题呢。比如在写武侠小说的时候,首先会想小说里边需要包含武侠、爱情、亲情、搞笑四个主题。并且给这四个主题分配一定的比例(如武侠0.4,爱情0.3,亲情0.2,搞笑0.1)。每个主题会包含一些word,不同word的概率也是不一样的。 因此我们上帝在生成一篇文章的时候流程是这个样子的:
(1)上帝有两个坛子的骰子,第一个坛子装的是doc-topic骰子,第二个坛子装的是topic-wod骰子。
(2)上帝随机的从二个坛子中独立抽取了k个topic-doc骰子,编号1-K。
(3)每次生成一篇新的文档前,上帝先从第一个坛子中随机抽取一个doc-topic骰子,然后重复如下过程生成文档中的词。
<1>、投掷这个doc-topic骰子,得到一个topic的编号z。
<2>、选择K个topic-word骰子中编号为z的的那个,投掷这个骰子, 于是就得到了这个词。
假设语料库中有M篇文章, 所有的word和对应的topic如下表示:
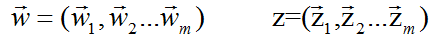
我们可以用下图来解释这个过程:

一共两个物理过程:
第一个过程:  ,这个过程分两个阶段。第一个阶段是上帝在生成一篇文档之前,先抽出一个主题分布的骰子
,这个过程分两个阶段。第一个阶段是上帝在生成一篇文档之前,先抽出一个主题分布的骰子 ,这个分布选择了狄利克雷分布(狄利克雷分布是多项分布的共轭分布)。 第二个阶段根据
,这个分布选择了狄利克雷分布(狄利克雷分布是多项分布的共轭分布)。 第二个阶段根据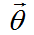 来抽样得到每个单词的topic。这是一个多项分布。 整个过程是符合狄利克雷分布的。
来抽样得到每个单词的topic。这是一个多项分布。 整个过程是符合狄利克雷分布的。
第二个过程: ,这个过程也分两个阶段。第一个阶段是对每个主题,生成word对应的概率,即选取的骰子
,这个过程也分两个阶段。第一个阶段是对每个主题,生成word对应的概率,即选取的骰子 ,这个分布也是选择了狄利克雷分布。 第二个阶段是根据
,这个分布也是选择了狄利克雷分布。 第二个阶段是根据 ,对于确定的主题选择对应的word,这是一个多项分布。因此,整个过程是狄利克雷分布。
,对于确定的主题选择对应的word,这是一个多项分布。因此,整个过程是狄利克雷分布。
4、吉普斯抽样概率公式推导
LDA的全概率公式为:  。 由于
。 由于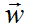 是观测到的已知数据,只有
是观测到的已知数据,只有 是隐含的变量,所以我们需要关注的分布为:
是隐含的变量,所以我们需要关注的分布为: 。 我们利用Gibbs Sampling进行抽样。 我们要求的某个位置i(m,n)对应的条件分布为
。 我们利用Gibbs Sampling进行抽样。 我们要求的某个位置i(m,n)对应的条件分布为 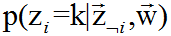 。
。
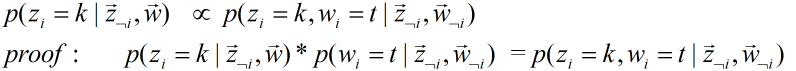
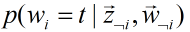 是一个定值,因此原公式成立。
是一个定值,因此原公式成立。
下边是公式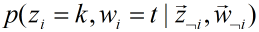 的推导:
的推导:
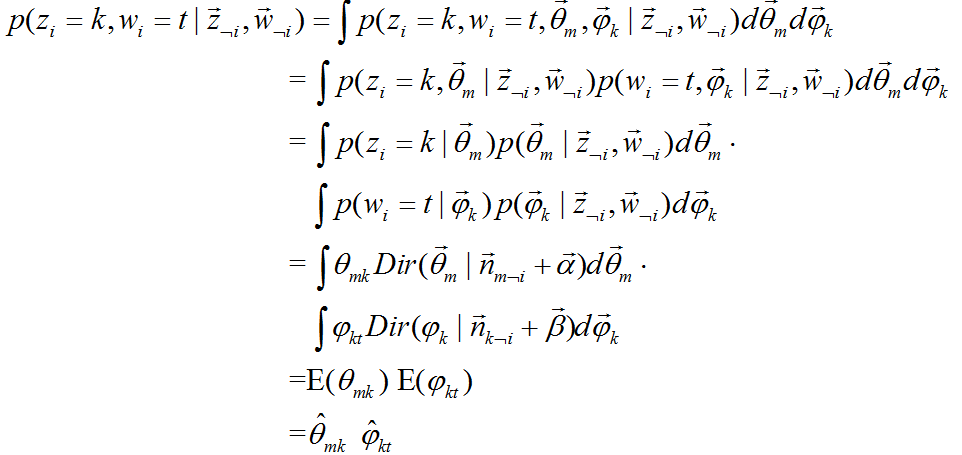
又由于根据狄利克雷分布的特性:
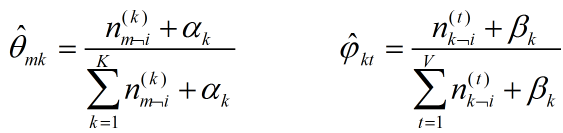

抽样的时候,首先随机给每个单词一个主题,然后用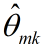 和
和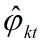 进行Gibbs抽样,抽样后更新这两个值,一直迭代到收敛(EM过程)。
进行Gibbs抽样,抽样后更新这两个值,一直迭代到收敛(EM过程)。
至此抽样就结束了。
5、使用LDA
抽样结束后,我们可以统计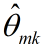 和
和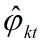 来得到
来得到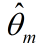 和
和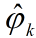 。
。
对于LDA我们的目标有两个:
(1)得到文章库中每篇文章的主题分布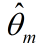
(2)对于一篇新来的文章,能得到它的主题分布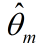 。
。
第一个目标很容易就能达到。下面主要介绍如果计算 一篇新文章的主题分布。这里我们假设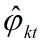 是不会变化的。因此对于一篇新文章到来之后,我们直接用Gibbs Sampling得到新文章的
是不会变化的。因此对于一篇新文章到来之后,我们直接用Gibbs Sampling得到新文章的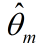 就好了。 具体抽样过程同上。
就好了。 具体抽样过程同上。
由于工程上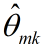 对于计算新的文章没有作用,因此往往只会保存
对于计算新的文章没有作用,因此往往只会保存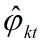 。
。
参考资料:
《LDA数学八卦》 Rickjin著
python LDA package:
http://pythonhosted.org/lda/index.html
LDA算法 (主题模型算法) 学习笔记的更多相关文章
- LDA(主题模型算法)
LDA整体流程 先定义一些字母的含义: 文档集合D,topic集合T D中每个文档d看作一个单词序列< w1,w2,...,wn >,wi表示第i个单词,设d有n个单词.(LDA里面称之为 ...
- Spark:聚类算法之LDA主题模型算法
http://blog.csdn.net/pipisorry/article/details/52912179 Spark上实现LDA原理 LDA主题模型算法 [主题模型TopicModel:隐含狄利 ...
- [综] Latent Dirichlet Allocation(LDA)主题模型算法
多项分布 http://szjc.math168.com/book/ebookdetail.aspx?cateid=1&§ionid=983 二项分布和多项分布 http:// ...
- 机器学习实战(Machine Learning in Action)学习笔记————06.k-均值聚类算法(kMeans)学习笔记
机器学习实战(Machine Learning in Action)学习笔记————06.k-均值聚类算法(kMeans)学习笔记 关键字:k-均值.kMeans.聚类.非监督学习作者:米仓山下时间: ...
- Spark机器学习(8):LDA主题模型算法
1. LDA基础知识 LDA(Latent Dirichlet Allocation)是一种主题模型.LDA一个三层贝叶斯概率模型,包含词.主题和文档三层结构. LDA是一个生成模型,可以用来生成一篇 ...
- RSA算法、SSL协议学习笔记
最近学习计算机网络,涉及到SSL协议,我想起了去年密码学课程讲过的非对称加密RSA算法,结合阮老师的博客,写写学习笔记,这里再回忆一下. RSA算法 RSA算法是一种非对称密码算法,所谓非对称,就是指 ...
- LDA概率主题模型
目录 LDA 主题模型 几个重要分布 模型 Unigram model Mixture of unigrams model PLSA模型 LDA 怎么确定LDA的topic个数? 如何用主题模型解决推 ...
- TF-IDF与主题模型 - NLP学习(3-2)
分词(Tokenization) - NLP学习(1) N-grams模型.停顿词(stopwords)和标准化处理 - NLP学习(2) 文本向量化及词袋模型 - NLP学习(3-1) 在上一篇博文 ...
- LDA(Latent Dirichlet Allocation)主题模型算法
原文 LDA整体流程 先定义一些字母的含义: 文档集合D,topic集合T D中每个文档d看作一个单词序列< w1,w2,...,wn >,wi表示第i个单词,设d有n个单词.(LDA里面 ...
随机推荐
- ZK中使用JS读取客户端txt文件内容问题
最近写一个需求时遇到一个问题,用户需要通过点击一个按钮直接读取他自己电脑上D盘的一个txt文件内容显示到页面,因为项目现在是用ZK写的.我对于ZK也是刚刚了解不就,很多都还不是很熟.起初我是想用io流 ...
- Java 之 方法引用
方法引用 一.冗余的Lambda场景 来看一个简单的函数式接口以应用Lambda表达式: @FunctionalInterface public interface Printable { void ...
- UCOSIII互斥信号量
互斥信号量可以解决优先级反转问题 优化后现象 优化方法:L和H等待同一个信号量的时候,将L任务优先级提至H相同优先级 实验举例 void start_task(void *p_arg) { OS_CR ...
- Struts框架笔记04_拦截器_标签库
目录 1. Struts2的拦截器 1.1 拦截器概述 1.2 拦截器的实现原理 1.3 Struts的执行流程 1.4 拦截器入门 1.4.1 环境搭建 1.4.2 编写拦截器 1.4.3 配置拦截 ...
- 批处理引擎MapReduce编程模型
批处理引擎MapReduce编程模型 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. MapReduce是一个经典的分布式批处理计算引擎,被广泛应用于搜索引擎索引构建,大规模数据处理 ...
- Integer Inquiry UVA-424(大整数)
题意分析: 将字符串倒着存入int数组中,每次加完后再取余除去大于10的部分 关键:倒着存入,这样会明显缩短代码量. #include<iostream> #include<cstd ...
- python_并发编程——管道
1.管道 from multiprocessing import Pipe conn1,conn2 = Pipe() #返回两个值 conn1.send('wdc') #发送 print(conn2. ...
- vue中超简单的方法实现点击一个按钮出现弹框,点击弹框外关闭弹框
效果图展示: View层 <template> <div> <div class="mask" v-if="showModal" ...
- 【C语言基础】编码规范
from:程序员互动联盟 2016-12-28 1. 基本要求 1.1 程序结构清析,简单易懂,单个函数的程序行数不得超过100行. 1.2 打算干什么,要简单,直接了当,代码精简,避免垃圾程序. ...
- python的优缺点。
Python的定位是“优雅”.“明确”.“简单”,所以Python程序看上去总是简单易懂,初学者学Python,不但入门容易,而且将来深入下去,可以编写那些非常非常复杂的程序. 开发效率非常高,Pyt ...
