最小二乘法 及python 实现
参考 最小二乘法小结 机器学习:Python 中如何使用最小二乘法
什么是” 最小二乘法” 呢
定义:最小二乘法(又称最小平方法)是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。
作用:利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
原则:以” 残差平方和最小” 确定直线位置 (在数理统计中,残差是指实际观察值与估计值之间的差)
数学公式: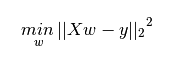
基本思路:对于一元线性回归模型, 假设从总体中获取了 n 组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn),对于平面中的这 n 个点,可以使用无数条曲线来拟合。而线性回归就是要求样本回归函数尽可能好地拟合这组值,也就是说,这条直线应该尽可能的处于样本数据的中心位置。因此,选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。 求最小,那就通过 对参数分别求导数联立方程组来解。
- 最小二乘法是直接利用最小化误差平法和,来对参数求导,求得参数解,属于比较确定的值
- 而 梯度下降法 ,属于迭代法,知道梯度 下降的方向刘,挨个去迭代。
1. 最小二乘法的原理与要解决的问题

2. 最小二乘法的代数法解法


3.最小二乘法的局限性和适用场景

##最小二乘法
import numpy as np ##科学计算库
import scipy as sp ##在numpy基础上实现的部分算法库
import matplotlib.pyplot as plt ##绘图库
from scipy.optimize import leastsq ##引入最小二乘法算法 '''
设置样本数据,真实数据需要在这里处理
'''
##样本数据(Xi,Yi),需要转换成数组(列表)形式
Xi=np.array([6.19,2.51,7.29,7.01,5.7,2.66,3.98,2.5,9.1,4.2])
Yi=np.array([5.25,2.83,6.41,6.71,5.1,4.23,5.05,1.98,10.5,6.3]) '''
设定拟合函数和偏差函数
函数的形状确定过程:
1.先画样本图像
2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
''' ##需要拟合的函数func :指定函数的形状
def func(p,x):
k,b=p
return k*x+b ##偏差函数:x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
return func(p,x)-y '''
主要部分:附带部分说明
1.leastsq函数的返回值tuple,第一个元素是求解结果,第二个是求解的代价值(个人理解)
2.官网的原话(第二个值):Value of the cost function at the solution
3.实例:Para=>(array([ 0.61349535, 1.79409255]), 3)
4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
''' #k,b的初始值,可以任意设定,经过几次试验,发现p0的值会影响cost的值:Para[1]
p0=[1,20] #把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi)) #读取结果
k,b=Para[0]
print("k=",k,"b=",b)
print("cost:"+str(Para[1]))
print("求解的拟合直线为:")
print("y="+str(round(k,2))+"x+"+str(round(b,2))) '''
绘图,看拟合效果.
matplotlib默认不支持中文,label设置中文的话需要另行设置
如果报错,改成英文就可以
''' #画样本点
plt.figure(figsize=(8,6)) ##指定图像比例: 8:6
plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2) #画拟合直线
x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color="red",label="拟合直线",linewidth=2)
plt.legend(loc='lower right') #绘制图例
plt.show()
结果如下所示:
输出结果:
k= 0.900458420439 b= 0.831055638877
cost:1
求解的拟合直线为:
y=0.9x+0.83
绘图结果:
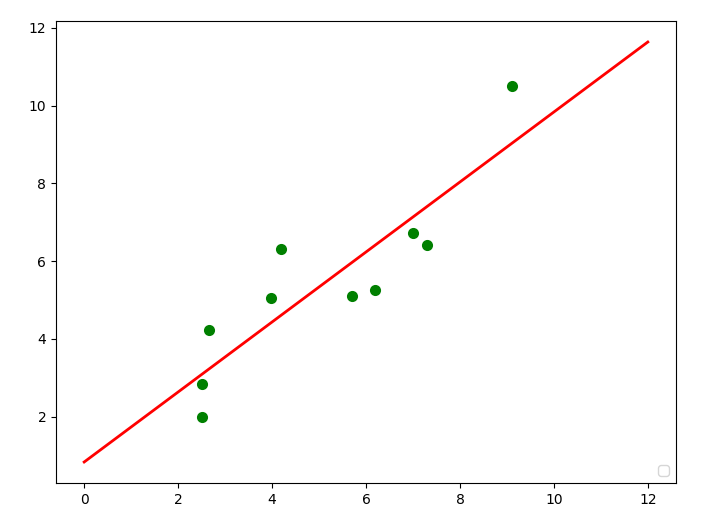
最小二乘法 及python 实现的更多相关文章
- 回归_最小二乘法(python脚本实现)
python机器学习-乳腺癌细胞挖掘(博主亲自录制视频) https://study.163.com/course/introduction.htm?courseId=1005269003& ...
- 简单线性回归(最小二乘法)python实现
简单线性回归(最小二乘法)¶ 0.引入依赖¶ In [7]: import numpy as np import matplotlib.pyplot as plt 1.导入数据¶ In [ ...
- 转悠望南山 Python闲谈(二)聊聊最小二乘法以及leastsq函数
1 最小二乘法概述 自从开始做毕设以来,发现自己无时无刻不在接触最小二乘法.从求解线性透视图中的消失点,m元n次函数的拟合,包括后来学到的神经网络,其思想归根结底全都是最小二乘法. 1-1 “多线 ...
- Python闲谈(二)聊聊最小二乘法以及leastsq函数
1 最小二乘法概述 自从开始做毕设以来,发现自己无时无刻不在接触最小二乘法.从求解线性透视图中的消失点,m元n次函数的拟合,包括后来学到的神经网络,其思想归根结底全都是最小二乘法. 1-1 “多线→一 ...
- 机器学习实战笔记(Python实现)-08-线性回归
--------------------------------------------------------------------------------------- 本系列文章为<机器 ...
- (转)梯度下降法及其Python实现
梯度下降法(gradient descent),又名最速下降法(steepest descent)是求解无约束最优化问题最常用的方法,它是一种迭代方法,每一步主要的操作是求解目标函数的梯度向量,将当前 ...
- python数据分析入门——matplotlib的中文显示问题&最小二乘法
正在学习<用python做科学计算>,在练习最小二乘法时遇到matplotlib无法显示中文的问题.查资料,感觉动态的加上几条语句是最好,这里贴上全部的代码. # -*- coding: ...
- 机器学习:Python中如何使用最小二乘法
之所以说"使用"而不是"实现",是因为python的相关类库已经帮我们实现了具体算法,而我们只要学会使用就可以了.随着对技术的逐渐掌握及积累,当类库中的算法已经 ...
- Python实现实现基于最小二乘法的线性回归
下面展示利用Python实现基于最小二乘法的线性回归模型,同时不需要引入其他科学计算以及机器学习的库. 利用Python代码表示如下: #首先引入数据集x,和y的值的大小利用Python的数据结构:列 ...
随机推荐
- POJ2125 Destroying The Graph
题目链接:ヾ(≧∇≦*)ゝ 大致题意: 给出一个有向图D=(V,E).对于每个点U,定义两种操作a(u),b(u) 操作a(u):删除点U的所有出边,即属于E,操作花费为Ca(u). 操作b(u):删 ...
- 【BZOJ1295】[SCOI2009]最长距离(最短路)
[BZOJ1295][SCOI2009]最长距离(最短路) 题面 BZOJ 洛谷 题解 这题很妙啊. 我们枚举一个点,只需要考虑到他的最远点就行了,显然只需要考虑一个点即可.那么这两个点之前联通的最小 ...
- 前端学习 -- Css -- 选择器的优先级
当使用不同的选择器,选中同一个元素时并且设置相同的样式时,这时样式之间产生了冲突,最终到底采用哪个选择器定义的样式,由选择器的优先级(权重)决定优先级高的优先显示. 优先级的规则 内联样式 , 优先级 ...
- 四、spring boot 1.5.4 日志管理
spring boot日志默认采用logback进行输出,你可以对logback进行定制化,方法如下: 在resources文件夹下建立logback.xml配置文件 <?xml version ...
- Eclipse启动项目正常,放到tomcat下单独启动就报错的 一例
一个老的ssh的项目,进行二次开发(增加一些新功能)后, 首先用Eclipse中集成的Tomcat启动没有任何问题,但是把启动后的webapps下得目录放到 windows的普通tomcat下单独启动 ...
- Flask script 内的Shell 类 使用
1.集成Python shell 每次自动shell会话都要导入数据库实例和模型,很烦人.为了避免一直重复导入,我们可以做些配置让Flask-Script的Shell命令自动导入特定的对象.若想把对象 ...
- Linux下使用cron让Python程序持久化运行
正常情况下,一个python程序如果希望实现一直运行,不出错不奔溃是很难的,即使编译为可持续文件也是一样 幸运的是很多需求并不是需要24小时不间断运行,而是每隔一段时间运行一次即可 Linux系统自带 ...
- Angular的依赖注入(依赖反转)原理说明
依赖注入(依赖反转)意思是由函数决定要引入什么样的依赖: let mod = angular.module('test',[]); mod.controller('test_c',function($ ...
- Java基础-SSM之mybatis一对多和多对一关系映射
Java基础-SSM之mybatis一对多和多对一关系映射 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 一.准备测试环境(创建数据库表) 1>.创建customers表: ...
- java基础-网络编程(Socket)技术选型入门之NIO技术
java基础-网络编程(Socket)技术选型入门之NIO技术 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 一.传统的网络编程 1>.编写socket通信的MyServer ...
