OpenJudge 求重要逆序对数

https://blog.csdn.net/mrvector/article/details/81090165

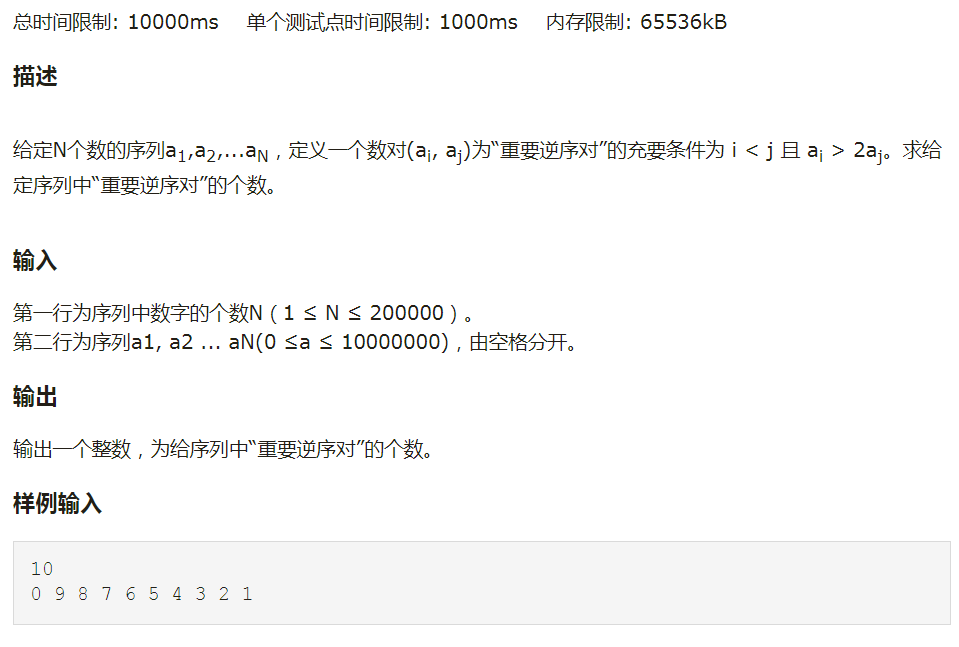
【题解】

方法与求逆序对的个数类似，用归并排序分治求解。不同之处在于添加了一个虚拟指针pointer。

【代码】

 #include <iostream>
 using namespace std;
 #define maxn 200005

 int s[maxn], temp[maxn];
 long long ans;

 void Merge(int left, int right, int mid)
 {
     int i = left, j = mid + , k = left;
     int pointer = left;
     while (i <= mid && j <= right) {
         if (s[i] > s[j]) {
             temp[k++] = s[j];
             while (pointer <= mid && s[pointer] <=  * s[j])
                 pointer++;
             if (pointer < mid + )
                 ans += mid - pointer + ;
             j++;
         }
         else {
             temp[k++] = s[i];
             i++;
         }
     }
     while (i <= mid)
         temp[k++] = s[i++];
     while (j <= right)
         temp[k++] = s[j++];
     for (int i = left; i <= right; i++)
         s[i] = temp[i];
 }

 void MergeSort(int left, int right)
 {
     int mid = (left + right) >> ;
     if (left < right) {
         MergeSort(left, mid);
         MergeSort(mid + , right);
         Merge(left, right, mid);
     }
 }

 int main()
 {
     int N;
     cin >> N;
     for (int i = ; i < N; i++)
         cin >> s[i];
     MergeSort(, N - );
     cout << ans << endl;
     //system("pause");
     return ;
 }