Bzoj4818:生成函数 快速幂

转来的题面: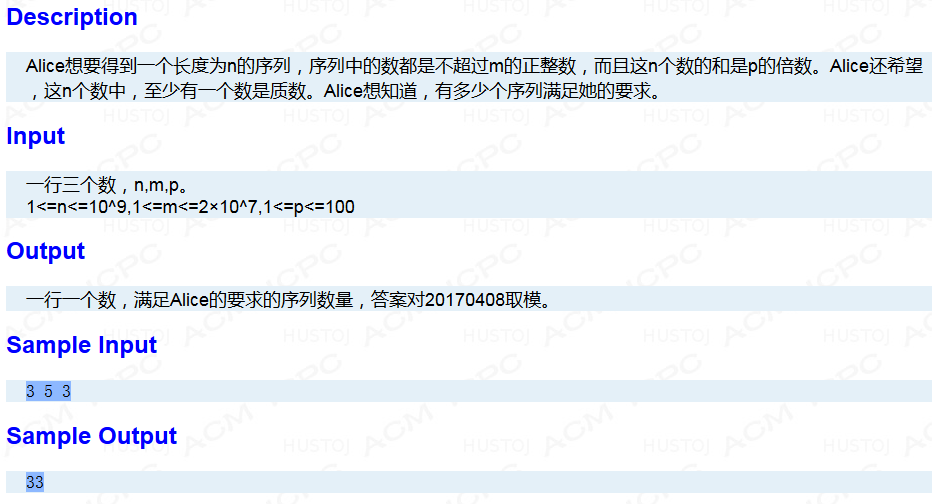

首先这题显然补集转化，就是用全部方案减去不含任何质数的方案。
然后怎么做呢?
考虑m比较小，我们能大力把<=m的质数全都筛出来。
发现n很大，要么倍增要么快速幂......
发现p相当小，所以我们能在mod p的同余系下做啊。

一看到同余系下求方案数立刻想到卷积和生成函数......
假设我们有一个多项式f(x)，其中x^i的系数为a个数的序列mod p为i的方案数(a为我们引入的变量)。
同时我们有另一个多项式g(x),其中x^i的系数为b个数的序列mod p为i的方案数(b为我们引入的变量)。
那么，我们如果让f(x)和g(x)做卷积的话，新的多项式x^i的系数就是(a+b)个数的序列mod p为i的方案数的说。
这就是生成函数了。

回到这个题，我们先初始化多项式f(x)，令x^i的系数为为1个数mod p为i的方案数。
然后我们求出这个多项式的n次方，就是我们需要的答案了。

发现这道题的p很小，我们连FFT都不用，直接用一个多项式类暴力快速幂就行了。复杂度O(m+p^2logn)，跑的飞起。

话说为什么p才100啊，如果修改一下模数然后NTT的话，可以做到p为1e5级别，n为1e18级别的。

代码:

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define debug cout
 typedef long long int lli;
 using namespace std;
 const int maxn=1e2+1e1,maxl=2e7+1e2,lim=2e7;
 const int mod=;

 bool vis[maxl];
 int p,m;

 struct Poly {
     lli dat[maxn];
     Poly() {
         memset(dat,,sizeof(dat));
     }
     lli& operator [] (const int &x) {
         return dat[x];
     }
     const lli& operator [] (const int &x) const {
         return dat[x];
     }
     friend Poly operator * (const Poly &a,const Poly &b) {
         Poly ret;
         for(int i=;i<p;i++) for(int j=;j<p;j++) {
             ( ret[(i+j)%p] += a[i] * b[j] % mod ) %= mod;
         }
         return ret;
     }
 }full,oly;

 inline void sieve() {
     static int prime[maxl],cnt;
     vis[] = ;
     for(int i=;i<=m;i++) {
         if( !vis[i] ) prime[++cnt] = i;
         for(int j=;j<=cnt&&(lli)i*prime[j]<=m;j++) {
             vis[i*prime[j]] = ;
             if( ! ( i % prime[j] ) ) break;
         }
     }
 }

 inline void init() {
     for(int i=;i<=m;i++) {
         full[i%p]++;
         if( vis[i] ) oly[i%p]++;
     }
 }

 inline Poly fastpow(Poly base,int tim) {
     Poly ret = base; --tim;
     while( tim ) {
         if( tim &  ) ret = ret * base;
         if( tim >>=  ) base = base * base;
     }
     return ret;
 }

 int main() {
     static int n;
     static lli ans;
     scanf("%d%d%d",&n,&m,&p) , sieve();
     init();
     full = fastpow(full,n) , oly = fastpow(oly,n);
     ans = ( full[] - oly[] + mod ) % mod;
     printf("%lld\n",ans);
     return ;
 }