KL散度与JS散度

1.KL散度

KL散度( Kullback–Leibler divergence)是描述两个概率分布P和Q差异的一种测度。对于两个概率分布P、Q，二者越相似，KL散度越小。

KL散度的性质：P表示真实分布，Q表示P的拟合分布

1. 非负性：KL(P||Q)>=0，当P=Q时，KL(P||Q)=0；
2. 反身性：KL(P||P)=0
3. 非对称性：D(P||Q) ≠ D(Q||P)
4. KL散度不满足三角不等

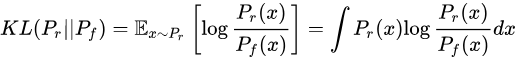
python 代码实现：

from scipy import stats

P = [0.2, 0.4, 0.4]
Q = [0.4, 0.2, 0.5]
print(stats.entropy(P,Q))

0.1446821953906301

KL散度很容易梯度消失，KL 散度假设这两个分布共享相同的支撑集（也就是说，它们被定义在同一个点集上）。如果2个分布相聚太远或者2个分布之间没有重叠，计算出来的值为无穷大。

2.JS散度

• JS散度的取值范围在0-1之间，完全相同时为0
• JS散度是对称的

from scipy import stats
import numpy as np
P =np.asarray( [[0.00934234 , 2.1068802],[0.01882005 , 2.03656788],[ 0.25182744 , 2.14507649]])

Q = np.asarray([[ 0.34670991, -0.24534987],[ 0.93025953 ,-0.69697827],[ 0.47976121, -0.33842087]])
M = (P+Q)/2
print(0.5*stats.entropy(P, M)+0.5*stats.entropy(Q, M))