SourceTree 3.1.3 版本跳过bitbucket注册方法（亲测好用）

1.首先下载并安装好git程序。

2.接着下载并执行SourceTreeSetup-3.1.3.exe，会进入登录或注册bitbucket的界面，我只是想用软件，并不想去注册账号。怎么办？请往下看。

3.

打开 %LocalAppData%\Atlassian目录，接着进入SourceTree目录，创建accounts.json文件，并修改accounts.json内容如下：

[

{

"$id": "1",

"$type": "SourceTree.Api.Host.Identity.Model.IdentityAccount, SourceTree.Api.Host.Identity",

"Authenticate": true,

"HostInstance": {

"$id": "2",

"$type": "SourceTree.Host.Atlassianaccount.AtlassianAccountInstance, SourceTree.Host.AtlassianAccount",

"Host": {

"$id": "3",

"$type": "SourceTree.Host.Atlassianaccount.AtlassianAccountHost, SourceTree.Host.AtlassianAccount",

"Id": "atlassian account"

},

"BaseUrl": "https://id.atlassian.com/"

},

"Credentials": {

"$id": "4",

"$type": "SourceTree.Model.BasicAuthCredentials, SourceTree.Api.Account",

"Username": "",

"Email": null

},

"IsDefault": false

}

]

4.

打开 %LocalAppData%\Atlassian，进入“SourceTree.exe_Url_iayhtc13zv3obzuz5vchezjs1az2q5ef”（注该目录可能和版本相关，不同版本的路径可能不完全一样。）

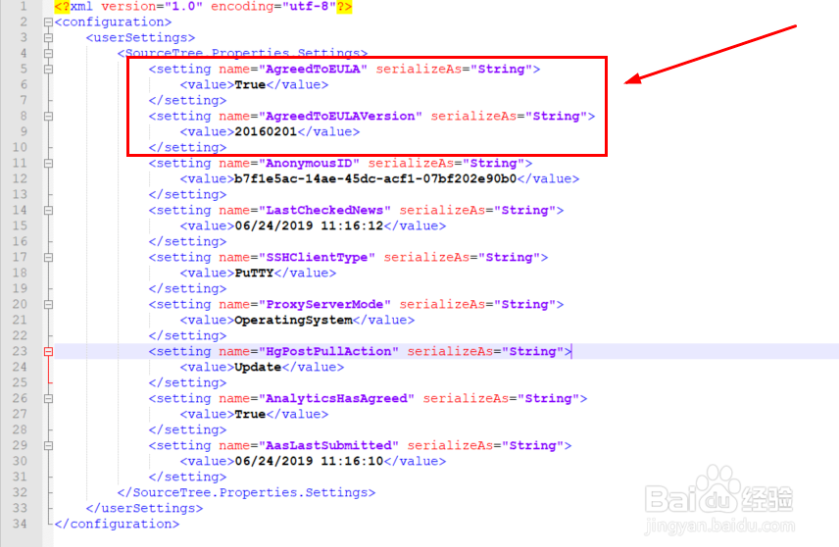
接着进入"3.1.3.3158"目录，打开user.config文件，在里面加入六行代码。

<setting name="AgreedToEULA" serializeAs="String">

                <value>True</value>

            </setting>

            <setting name="AgreedToEULAVersion" serializeAs="String">

                <value></value>

            </setting>

5

再次执行SourceTreeSetup-3.1.3.exe，此处可能会出现如下二种情况，

情况一就进入下一步安装。

第二种情况

选择第四个

6。完成安装，过程跳过繁琐的bitbucket注册。 ：）

搞定。

本文参考地址：https://jingyan.baidu.com/article/4f34706e6e4985e386b56d79.html 百度经验