[hdu5372 Segment Game]树状数组

题意：有两种操作：(1)插入线段，第i次插入的线段左边界为Li，长度为i (2)删除线段，删除第x次插入的线段。每次插入线段之前询问有多少条线段被它覆盖。

思路：由于插入的线段长度是递增的，所以第i次插入的线段的长度比以前插入的所有线段都要长，从以前插入的线段里面任取一条，考虑其与当前线段的位置关系，主要有以下三种：

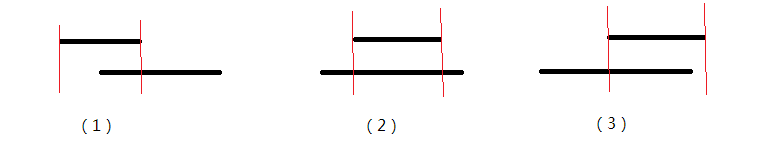
图中，下方表示当前线段。注意到，只有被当前线段覆盖的线段，它的左右边界和当前线段的左右边界的相对位置是不同的。也就是说，查询有多少个线段的右端点小于等于该线段右端点，再查询有多少条线段左端点小于该线段的左端点， 两者之差就是答案。因为不符合要求的线段同时进入了前者和后者，而符合要求的答案只进入了前者。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128

//#pragma comment(linker, "/STACK:1024000000") #include <map> #include <set> #include <cmath> #include <ctime> #include <deque> #include <queue> #include <stack> #include <vector> #include <cstdio> #include <string> #include <cstdlib> #include <cstring> #include <iostream> #include <algorithm> using namespace std; #define X first #define Y second #define pb push_back #define mp make_pair #define all(a) (a).begin(), (a).end() #define fillchar(a, x) memset(a, x, sizeof(a)) #define copy(a, b) memcpy(a, b, sizeof(a)) typedef long long ll; typedef pair<int, int> pii; typedef unsigned long long ull; //#ifndef ONLINE_JUDGE void RI(vector<int>&a,int n){a.resize(n);for(int i=;i<n;i++)scanf("%d",&a[i]);} void RI(){}void RI(int&X){scanf("%d",&X);}template<typename...R> void RI(int&f,R&...r){RI(f);RI(r...);}void RI(int*p,int*q){int d=p<q?:-; while(p!=q){scanf("%d",p);p+=d;}}void print(){cout<<endl;}template<typename T> void print(const T t){cout<<t<<endl;}template<typename F,typename...R> void print(const F f,const R...r){cout<<f<<", ";print(r...);}template<typename T> void print(T*p, T*q){int d=p<q?:-;while(p!=q){cout<<*p<<", ";p+=d;}cout<<endl;} //#endif template<typename T>bool umax(T&a, const T&b){return b<=a?false:(a=b,true);} template<typename T>bool umin(T&a, const T&b){return b>=a?false:(a=b,true);} template<typename T> void V2A(T a[],const vector<T>&b){for(int i=;i<b.size();i++)a[i]=b[i];} template<typename T> void A2V(vector<T>&a,const T b[]){for(int i=;i<a.size();i++)a[i]=b[i];} #if 0 const double PI = acos(-1.0); const int INF = 1e9 + 7; const double EPS = 1e-8; #endif /* -------------------------------------------------------------------------------- */ const int maxn = 4e5 + ; int u[maxn], v[maxn], w[maxn], tot; pii rem[maxn]; class TA { int C[maxn], n; inline int lowbit(int x) { return x & -x; } public: void init(int n) { this->n = n; for (int i = ; i <= n; i ++) C[i] = ; } void update(int p, int x) { while (p <= n) { C[p] += x; p += lowbit(p); } } int query(int p) { int ans = ; while (p) { ans += C[p]; p -= lowbit(p); } return ans; } }; TA lta, rta; inline int find(int x) { return lower_bound(w, w + tot, x) - w + ; } int main() { #ifndef ONLINE_JUDGE freopen("in.txt", "r", stdin); //freopen("out.txt", "w", stdout); #endif // ONLINE_JUDGE int cas = , n; while (cin >> n) { tot = ; int len = ; for (int i = ; i < n; i ++) { scanf("%d%d", u + i, v + i); if (u[i] == ) { rem[len] = mp(v[i], v[i] + len); w[tot ++] = v[i]; w[tot ++] = v[i] + len ++; } } sort(w, w + tot); tot = unique(w, w + tot) - w; lta.init(tot); rta.init(tot); printf("Case #%d:\n", ++ cas); len = ; for (int i = ; i < n; i ++) { if(u[i] == ) { pii buf = rem[v[i]]; int lid = find(buf.X), rid = find(buf.Y); lta.update(lid, - ); rta.update(rid, - ); } else { int lid = find(v[i]), rid = find(v[i] + len ++); printf("%d\n", rta.query(rid) - lta.query(lid - )); lta.update(lid, ); rta.update(rid, ); } } } return ; }