Knapsack Problem

0-1背包

• 描述：N件物品，第i件的重量是w[i]，价值v[i]。有一个容量为W的背包，求将哪些物品放入背包可使总价值最大。每件物品可以用0或1次。
• 分析：根据题意，可以写出表达式：

\[max(\Sigma v_ix_i), s.t. \Sigma w_ix_i<=W, x_i\in\{0, 1\}
\]

最直接的思路就是：对于每件物品，都有yes/no两种选择，尝试所有的组合，记录每个组合的价值，选出满足重量条件的最大价值。时间复杂度\(O(2^n)\)，空间复杂度\(O(n)\)。

// backtracking
class knapsack01 {
public:
	int knapsack(int W, vector<int>& w, vector<int>& v, string& ans) {
		string cur(w.size(), '0');

		dfs(0, 0, 0, W, w, v, cur, ans);
		return maxV;
	}
private:
	void dfs(int s, int curW, int curV, int W, vector<int>& w, vector<int>& v, string& cur, string& ans) {
		// 到达叶子结点，得到一个解，所以在这里更改最终结果
		if (s >= w.size()) {
			if (maxV < curV) {
				ans.assign(cur);
				maxV = curV;
			}
			return;
		}

		// as for goods s, two choices
		for (int i = 0; i < 2; ++i) {
			cur[s] = i + '0';

			if (curW + i * w[s] <= W) {
				curW += i * w[s];
				curV += i * v[s];
				dfs(s + 1, curW, curV, W, w, v, cur, ans);
				curW -= i * w[s];
				curV -= i * v[s];
			}
		}
	}

	int maxV = 0;
};

上面的程序可以通过剪枝进行优化，下来换一种思路：

令dp[i][j]表示前i件物品重量恰好为j时具有的最大价值，问题转化为求dp[N][0...W]的最大值，边界条件dp[0...N][0]=0：

假设3件物品，\(w=\{1,1,2\}\)，\(v=\{1,2,4\}\)，\(W=2\)，先用递归形式分析，每件物品只有yes/no两种状态：



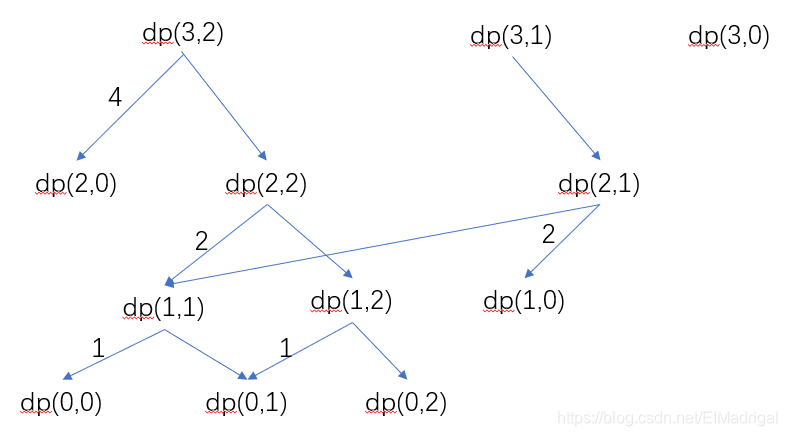
可以看到，求解过程中有很多重叠子问题，故可以采用记忆化递归求解，时间复杂度即为子问题数量\(O(NW)\)，空间复杂度\(O(NW)\)。

记忆化递归可以写成自底向上的动态规划，状态转移方程：

\[dp[i][j]=max\{dp[i-1][j], v[i]+dp[i-1][j-w[i]]\}
\]

// dp->space complexity O(NW)
class knapsack01 {
public:
	int knapsack(int W, vector<int>& w, vector<int>& v) {
		const int N = w.size();
		vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));
		for(int i = 1;i <= N;++i)
			for (int j = w[i - 1]; j <= W; ++j) {
				dp[i][j] = max(dp[i - 1][j], v[i - 1] + dp[i - 1][j - w[i - 1]]);
			}

		return *max_element(dp[N].begin(), dp[N].end());
	}
};

前i件物品只依赖于前i-1件物品，\(dp\)数组的更新方向为：



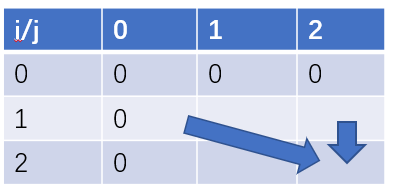
所以可以使用滚动数组降低空间复杂度为\(O(W)\)：

// dp->space complexity O(W)
// method 1: use temp array
class knapsack01 {
public:
	int knapsack(int W, vector<int>& w, vector<int>& v) {
		const int N = w.size();
		vector<int> dp(W + 1, 0);
		for (int i = 1; i <= N; ++i) {
			vector<int> temp(W + 1, 0);
			for (int j = w[i - 1]; j <= W; ++j) {
				temp[j] = max(temp[j], v[i - 1] + dp[j - w[i - 1]]);
			}
			dp.swap(temp);
		}

		return *max_element(dp.begin(), dp.end());
	}
};

// method 2: use scrolling array
class knapsack01 {
public:
	int knapsack(int W, vector<int>& w, vector<int>& v) {
		const int N = w.size();
		vector<int> dp(W + 1, 0);
		for (int i = 1; i <= N; ++i) {
			// iterate j reversely, avoid dp override
			for (int j = W; j >= w[i - 1]; --j) {
				dp[j] = max(dp[j], v[i - 1] + dp[j - w[i - 1]]);
			}
		}

		return *max_element(dp.begin(), dp.end());
	}
};

完全背包

• 每件物品可以使用任意多次。
• 一个Naive的思路： 虽然题目描述每件物品可以使用任意多次，但实际上由于W的限制，每件物品最多使用\(\lfloor W/w[i] \rfloor\)次。这样我们可以将每件物品拆为\(\lfloor W/w[i] \rfloor\)件，问题就转化为了0-1背包。子问题仍然有NW个，但是求解每个子问题需要\(O(W/w[i])\)，总的时间复杂度\(O(\Sigma (W/w[i])*W)\)，也即\(O(W*拆后物品件数)\)。
• 更tricky的做法：W无法改变，只能改变拆后物品件数。这里可以使用二进制的思想：假设我们某件物品可以使用\(10=8+2\)次，原本需要复制出10件，现在只要复制出2件，价值和重量是原来的8倍和2倍，这样就降低了复杂度。
• 完全背包有\(O(NW)\)的算法。

多重背包

• 每件物品最多可以使用\(num[i]\)次。
• 同样，Naive的思路就是将每件物品都复制\(num[i]\)次，问题转化为0-1背包，复杂度\(O(\Sigma nums[i]*W)\)。
• 将\(num[i]\)用二进制表示，价值和重量变为原来的相应倍，降低复杂度。

Future

后续还有混合背包、二维费用的背包等，详情可以学习背包九讲。