luogu P2280 激光炸弹(二维前缀和)

由题给的xi, yi范围,可以建立二维地图maze[i][j],记录i j范围上的所有目标的价值总和 即有maze[xi][yi] += wi

然后接下来的目标就是求出该二维数组的前缀和

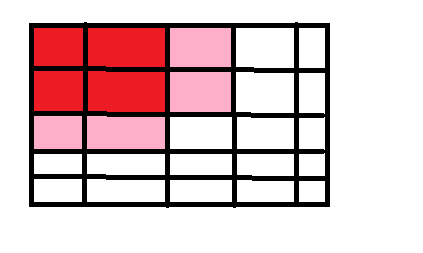
可得到前缀和计算的递推式: maze[i][j] += maze[i-1][j] + maze[i][j-1]-maze[i-1][j-1]

继而可以推出 对于一个边长为r的正方形其覆盖范围价值为 maze[i][j] - maze[i-r][j] - maze[i][j-r] + maze[i-r][j-r]

完整代码如下:

#include <bits/stdc++.h>
using namespace std;

int maze[][];

int main() {
    int n, r;
    scanf("%d%d", &n, &r);
    int a = r, b = r;
    for(int i = , x, y, w; i < n; i++) {
       scanf("%d%d%d", &x, &y, &w);
       x++, y++;
       a = max(a, x);
       b = max(b, y);
       maze[x][y] += w;
    }
    for(int i = ; i <= a; i++)
        for(int j = ; j <= b; j++)
            maze[i][j] += maze[i-][j] + maze[i][j-] - maze[i-][j-];

    int res = ;
    for(int i = r; i <= a; i++)
        for(int j = r; j <= b; j++)
            res = max(res, maze[i][j] - maze[i-r][j] - maze[i][j-r] + maze[i-r][j-r]);

    printf("%d\n", res);
}