红黑树的插入Java实现

package practice;

public class TestMain {
    public static void main(String[] args) {
        int[] ao = {5, 1, 18, 3, 8, 20, 13, 16, 12};
        Integer[] a = new Integer[9];
        for (int i = 0; i < a.length; i++) {
            a[i] = new Integer(ao[i]);
        }
        RedBlackBST<Integer,String> tree= new RedBlackBST<Integer,String>();
        for (int i = 0; i < a.length; i++) {
            tree.put(a[i], a[i].toString());
        }

        tree.print();
    }
}
/*
 * 红黑树
 * 与2-3树比较，红链接即表示像2-3树中的3-节点4-节点一样在"同一位置"（将红链接画平）
 */
class RedBlackBST <K extends Comparable<K>, V> {
    private static final boolean RED   = true;
    private static final boolean BLACK = false;

    private Node root;

    private class Node{
        K key;
        V value;
        Node left, right;
        int N;
        boolean color;

        public Node(K key, V value, int N, boolean color) {
            this.key   = key;
            this.value = value;
            this.N     = N;
            this.color = color;
        }
    }
    /*
     * 插入节点
     */
    public void put(K key, V value) {
        root = put(root, key, value);
    }
    private Node put(Node node, K key, V value) {
        if (node == null) { return new Node(key, value, 1, RED);}
        /*
         * 前面部分与二叉树插入一致，红黑树就是像二叉树一样插入后进行调整（旋转，颜色转换）
         */
        if (compare(key, node.key) < 0)      { node.left = put(node.left, key, value);}
        else if (compare(key, node.key) > 0) { node.right = put(node.right, key, value);}
        else                                 { node.value = value;}
        /*
         * 这里的旋转就是为了保证"同一位置"（即一个节点有两条红链接）的三个节点由从小到大排序且中间的节点连着他们的父节点
         * 颜色转换即是2-3树中的"向上增长"
         */
        if (!isRed(node.left)&&isRed(node.right))    { node = rorateLeft(node);} //左旋
        if (isRed(node.left)&&isRed(node.left.left)) { node = rorateRight(node);} //右旋
        if (isRed(node.left)&&isRed(node.right))     { flipColors(node);} //颜色转换

        node.N = size(node.left) + size(node.right) + 1;
        return node;
    }
    /*
     * 节点左旋 父节点为dad 红节点为son（dad为动图中的E son为图中的S）
     * 当右子节点是红色而左子节点是黑色，就以本节点为dad，右子节点为son进行左旋
     */
    private Node rorateLeft(Node dad) {
        Node son = dad.right;
        dad.right = son.left;
        son.left = dad;
        son.color = dad.color;
        dad.color = RED;
        son.N = dad.N;
        dad.N = size(dad.left) + size(dad.right) +1;
        return son;
    }
    /*
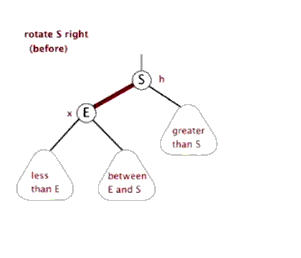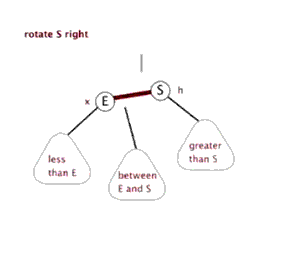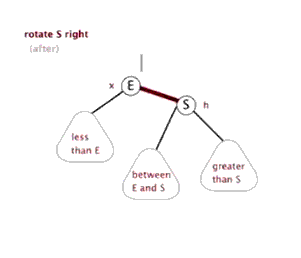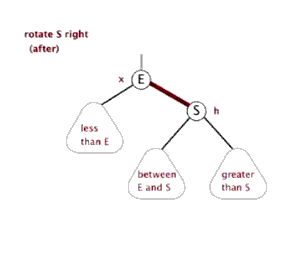
     * 节点右旋 父节点为dad 红节点为son
     * 当左子节点是红色且它的左子节点也是红色，就以本节点为dad，左子节点为son进行右旋
     */
    private Node rorateRight(Node dad) {
        Node son = dad.left;
        dad.left = son.right;
        son.right = dad;
        son.color = dad.color;
        dad.color = RED;
        son.N = dad.N;
        dad.N = size(dad.left) + size(dad.right) +1;
        return son;
    }
    /*
     * 颜色转换
     * 如果这个节点的左右子节点都为红色，就把他们都变为黑色，然后把自己变成红色
     */
    private void flipColors(Node node) {
        node.color = RED;
        node.left.color = BLACK;
        node.right.color =BLACK;
    }
    /*
     * 是否为红
     */
    private boolean isRed(Node node) {
        if (node == null) { return false;}
        return node.color == RED;
    }
    /*
     * 树的大小
     */
    private int size(Node node) {
        if (node == null) { return 0;}
        else              { return node.N;}
    }
    /*
     * key1 <  key2 -1
     * key1 >  key2  1
     * key1 == key2  0
     */
    private int compare(K key1, K key2) {
        return key1.compareTo(key2);
    }
    public void print() {
        print(root);
    }
    private void print(Node node) {
        if (node == null) {
            return;
        }
        print(node.left);
        System.out.println("key = "+node.key+" node.N = "+node.N);
        print(node.right);
    }

}

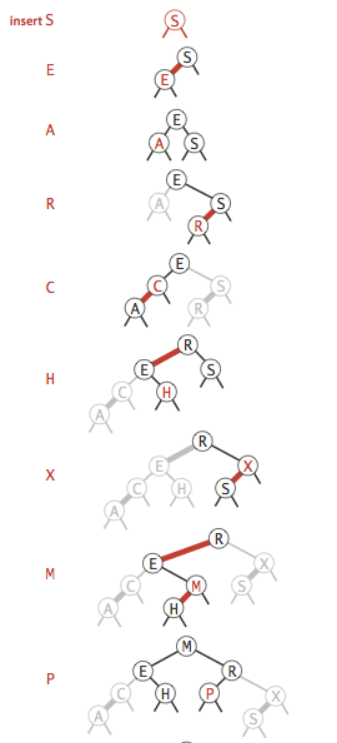
插入图示(S,E,A,R,C,H,X,M,P对应5,1,18,3,8,20,13,16)

左旋转

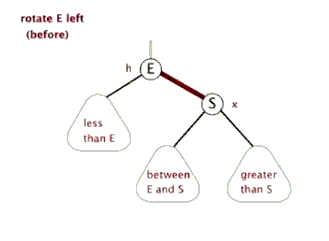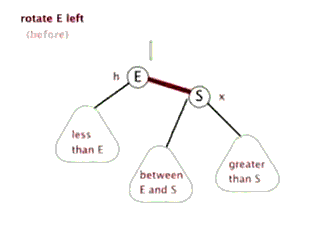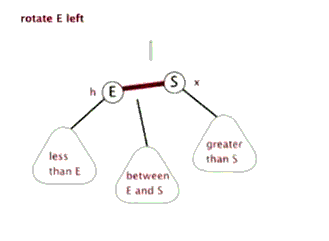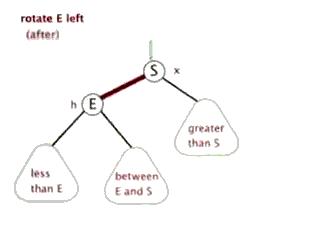
右旋转

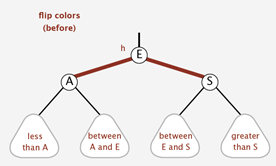
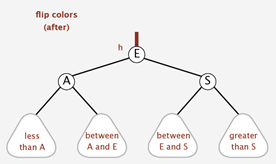
颜色转换