数据结构-二叉树 C和C++实现

二叉树，指针域具有两个“下一节点域”的特殊链表结构。

先来看看它的结构

来看程序中需要使用到的概念：

1、基本概念：

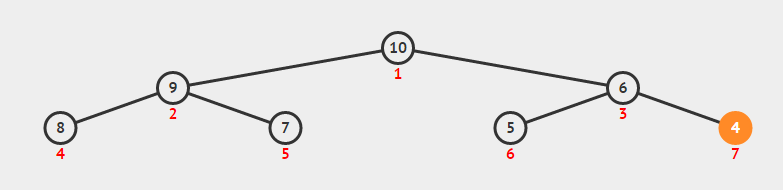
树根：二叉树的第一个节点,如图“10”为树根，也叫根节点

子树：对于某一个节点指针域指向的节点，左指针指向的节点为左子节点，右指针指向的节点为右子节点

树高：树的层数，如图树高为3

树宽：树在最多节点一层的节点数，如图树宽为4

叶子：不具有子树的节点，如图有4个叶子，分别为8、7、5、4

2、树的形态：

满二叉树：每一层上的节点数都是当层的最大节点数的二叉树，如上图为一颗满二叉树。

完全二叉树：对于一颗满二叉树，从右往左删除它的叶子节点，那么任意这样子的树都称为完全二叉树。若图中橙色的“4”删除掉，则为完全二叉树。

3、遍历方法：

先序遍历：按照“根->左子树->右子树”的顺序遍历数据。如图遍历顺序为（黑色数字）：10，9，8，7，6，5，4

中序遍历：按照“左子树->根->右子树”的顺序遍历数据。如图遍历顺序为（黑色数字）：8，9，7，10，5，6，4

后序遍历：按照“左子树->右子树->根”的顺序遍历数据。如图遍历顺序为（黑色数字）：8，7，9，5，4，6，10

---

---

---

C语言版本

C语言版本测试中用开头图中的例子：

如图这棵树有7个节点，红色数字为节点编号，圆圈内黑色数字为节点的值。

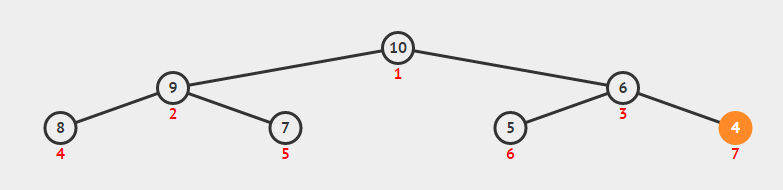
包含BiTreeNode、BinaryTree、Queue三个部分。main中为测试程序。

BiTreeNode为数的节点操作、BinaryTree为树本身的操作。Queue只用于统计宽度。

树的重要程序文件：

BiTreeNode.c:

#include <string.h>
#include "BiTreeNode.h"

bool BiTreeNode_Reset(BiTreeNode *node,int index, TreeElem data);
bool BiTreeNode_Delete(BiTreeNode *node);
int BiTreeNode_getIndex(BiTreeNode *node);
TreeElem BiTreeNode_getData(BiTreeNode *node);
BiTreeNode *BiTreeNode_getParent(BiTreeNode *node);
BiTreeNode *BiTreeNode_getLChild(BiTreeNode *node);
BiTreeNode *BiTreeNode_getRChild(BiTreeNode *node);
bool BiTreeNode_setIndex(BiTreeNode *node,int index);
bool BiTreeNode_setData(BiTreeNode *node,TreeElem data);
bool BiTreeNode_setParenet(BiTreeNode *node,BiTreeNode *parent);
bool BiTreeNode_setLChild(BiTreeNode *node,BiTreeNode *child);
bool BiTreeNode_setRChild(BiTreeNode *node,BiTreeNode *child);

BiTreeNode *BiTreeNode_NodeSearch(BiTreeNode *node,int index);
int NodeLeavesStatistics(BiTreeNode *Node,int leaves);//统计叶子数
int NodeChildrenNodeHeigh(BiTreeNode *Node); //统计子节点的最大高度（包含本节点）/（以本节点作为根求树的高度）

void BiTreeNode_PreorderTraversal(BiTreeNode *node);
void BiTreeNode_InorderTraversal(BiTreeNode *node);
void BiTreeNode_SubsequentTraversal(BiTreeNode *node);

bool BiTreeNode_Reset(BiTreeNode *node,int index, TreeElem data)
{
    if(node == NULL)
    {
         return false;//please malloc first.
    }
    node->iIndex = index;
    node->tData = data;
    node->pParent = NULL;
    node->pLeftChild = NULL;
    node->pRightChild = NULL;
    return true;
}

bool BiTreeNode_Delete(BiTreeNode *node)
{
    if(node == NULL)
    {
        return false;
    }
    if(node->pLeftChild != NULL)
    {
        BiTreeNode_Delete(node->pLeftChild);
        node->pLeftChild = NULL;
    }
    if(node->pRightChild != NULL)
    {
        BiTreeNode_Delete(node->pRightChild);
        node->pRightChild = NULL;
    }
    node->pParent = NULL;
    free(node);
    return true;
}

int BiTreeNode_getIndex(BiTreeNode *node)
{
    return node->iIndex;
}

TreeElem BiTreeNode_getData(BiTreeNode *node)
{
    return node->tData;
}

BiTreeNode *BiTreeNode_getParent(BiTreeNode *node)
{
    return node->pParent;
}
BiTreeNode *BiTreeNode_getLChild(BiTreeNode *node)
{
    return node->pLeftChild;
}
BiTreeNode *BiTreeNode_getRChild(BiTreeNode *node)
{
    return node->pRightChild;
}
bool BiTreeNode_setIndex(BiTreeNode *node,int index)
{
    if(node == NULL)
    {
        return false;
    }

    node->iIndex = index;
    return true;
}
bool BiTreeNode_setData(BiTreeNode *node,TreeElem data)
{
    if(node==NULL)
    {
        return false;
    }

    node->tData = data;
    return true;
}
bool BiTreeNode_setParenet(BiTreeNode *node,BiTreeNode *parent)
{
    node->pParent = parent;
    return true;
}
bool BiTreeNode_setLChild(BiTreeNode *node,BiTreeNode *child)
{
    node->pLeftChild = child;
    return true;
}
bool BiTreeNode_setRChild(BiTreeNode *node,BiTreeNode *child)
{
    node->pRightChild = child;
    return true;
}

BiTreeNode *BiTreeNode_NodeSearch(BiTreeNode *node,int index)
{
    BiTreeNode  *tempNode = NULL;
    if(node->iIndex == index)
    {
        return node;
    }
    if(node->pLeftChild != NULL)
    {
        tempNode = BiTreeNode_NodeSearch(node->pLeftChild,index);
        if(tempNode != NULL)
        {
            return tempNode;
        }
    }
    if(node->pRightChild != NULL)
    {
        tempNode = BiTreeNode_NodeSearch(node->pRightChild,index);
        if(tempNode != NULL)
        {
            return tempNode;
        }
    }
    return NULL;
}

int NodeLeavesStatistics(BiTreeNode *Node,int leaves)//统计叶子数
{
    if(Node->pLeftChild != NULL)
    {
        leaves = NodeLeavesStatistics(Node->pLeftChild,leaves);
    }
    if(Node->pRightChild != NULL)
    {
        leaves = NodeLeavesStatistics(Node->pRightChild,leaves);
    }
    if(Node->pLeftChild == NULL && Node->pRightChild == NULL)
    {
        leaves ++;
    }
    return leaves;
}

int NodeChildrenNodeHeigh(BiTreeNode *Node) //统计子节点的最大高度（包含本节点）/（以本节点作为根求树的高度）
{
    int heightLeft = ;
    int heightRight =;
    if(Node->pLeftChild != NULL)
    {
        heightLeft += NodeChildrenNodeHeigh(Node->pLeftChild);
    }
    if(Node->pRightChild != NULL)
    {
        heightRight += NodeChildrenNodeHeigh(Node->pRightChild);
    }
    if(heightRight > heightLeft)
    {
        return ++heightRight;
    }
    else
    {
        return ++heightLeft;
    }
}

int NodeChildrenStatistics(BiTreeNode *node)//统计子节点数（包括本节点）
{
    int iCnt=;
    if(node->pLeftChild != NULL)
    {
        iCnt+=NodeChildrenStatistics(node->pLeftChild);
    }
    if(node->pRightChild!= NULL)
    {
        iCnt+=NodeChildrenStatistics(node->pRightChild);;
    }
    iCnt++;
    return iCnt;
}

//traversal
void BiTreeNode_PreorderTraversal(BiTreeNode *node)
{
    printf("Index:%d,Data:%d\r\n",node->iIndex ,node->tData);

    if(node->pLeftChild != NULL)
    {
        BiTreeNode_PreorderTraversal(node->pLeftChild);
    }

    if(node->pRightChild != NULL)
    {
        BiTreeNode_PreorderTraversal(node->pRightChild);
    }
}
void BiTreeNode_InorderTraversal(BiTreeNode *node)
{
    if(node->pLeftChild != NULL)
    {
        BiTreeNode_InorderTraversal(node->pLeftChild);
    }

    printf("Index:%d,Data:%d\r\n",node->iIndex ,node->tData);

    if(node->pRightChild != NULL)
    {
        BiTreeNode_InorderTraversal(node->pRightChild);
    }
}
void BiTreeNode_SubsequentTraversal(BiTreeNode *node)
{
    if(node->pLeftChild != NULL)
    {
        BiTreeNode_SubsequentTraversal(node->pLeftChild);
    }

    if(node->pRightChild != NULL)
    {
        BiTreeNode_SubsequentTraversal(node->pRightChild);
    }

    printf("Index:%d,Data:%d\r\n",node->iIndex ,node->tData);
}

BiTreeNode.h:

#ifndef _BITREENODE_H
#define _BITREENODE_H
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include "Mystdbool.h"

typedef int TreeElem;

/*节点定义*/
typedef struct bitreenode
{
    TreeElem tData;
    int iIndex;
    struct bitreenode *pParent;
    struct bitreenode *pLeftChild;
    struct bitreenode *pRightChild;
}BiTreeNode;

//create and delete
bool BiTreeNode_Reset(BiTreeNode *node,int index ,TreeElem data);
bool BiTreeNode_Delete(BiTreeNode *node);
//get
int BiTreeNode_getIndex(BiTreeNode *node);
TreeElem BiTreeNode_getData(BiTreeNode *node);
BiTreeNode *BiTreeNode_getParent(BiTreeNode *node);
BiTreeNode *BiTreeNode_getLChild(BiTreeNode *node);
BiTreeNode *BiTreeNode_getRChild(BiTreeNode *node);
//set
bool BiTreeNode_setIndex(BiTreeNode *node,int index);
bool BiTreeNode_setData(BiTreeNode *node,TreeElem data);
bool BiTreeNode_setParenet(BiTreeNode *node,BiTreeNode *parent);
bool BiTreeNode_setLChild(BiTreeNode *node,BiTreeNode *child);
bool BiTreeNode_setRChild(BiTreeNode *node,BiTreeNode *child);
//search and statistics
BiTreeNode *BiTreeNode_NodeSearch(BiTreeNode *node,int index);
int NodeLeavesStatistics(BiTreeNode *Node,int leaves);//统计叶子数
int NodeChildrenNodeHeigh(BiTreeNode *Node); //统计子节点的最大高度（包含本节点）/（以本节点作为根求树的高度）
int NodeChildrenStatistics(BiTreeNode *node);//统计子节点数（包括本节点）
//Traversal
void BiTreeNode_PreorderTraversal(BiTreeNode *node);
void BiTreeNode_InorderTraversal(BiTreeNode *node);
void BiTreeNode_SubsequentTraversal(BiTreeNode *node);
#endif

BinaryTree.c

#include "BinaryTree.h"

bool BinaryTreeCreate(BinaryTree *tree,int size,int rootdata);
bool BinaryTreeDelete(BinaryTree *tree);
bool IsTreeFull(BinaryTree *tree);
//search and statistics
BiTreeNode* getNodeByIndex(BinaryTree *tree,int index);
int getLeaves(BinaryTree *tree);
int getHeight(BinaryTree *tree);
int getWidth(BinaryTree *tree);
int getTreeNodeNumber(BinaryTree *tree);
int getTreeMaxCapacity(BinaryTree *tree);
//add and delete
bool addLeftNodeByNode(BinaryTree *tree,int index,TreeElem data,BiTreeNode *pNode);    //添加左子树（使用父节点地址）
bool addRightNodeByNode(BinaryTree *tree,int index,TreeElem data,BiTreeNode *pNode);     //添加右子树（使用父节点地址）
bool addLeftNodeByIndex(BinaryTree *tree,int newIndex,TreeElem data,int searchIndex);    //添加左子树（使用索引）
bool addRightNodeByIndex(BinaryTree *tree,int newIndex,TreeElem data,int searchIndex);   //添加右子树（使用索引）
bool deleteNodeByNode(BinaryTree *tree,BiTreeNode *pNode);
bool deleteNodeByIndex(BinaryTree *tree,int index);
//traversal
void PreorderTraversal(BinaryTree *tree);                                            //先序遍历
void InorderTraversal(BinaryTree *tree)    ;                                            //中序遍历
void SubsequentTraversal(BinaryTree *tree);                                            //后序遍历

//create
bool BinaryTreeCreate(BinaryTree *tree,int size,int rootdata)
{
    tree->iMaxSize = size;
    tree->iSize=;
    tree->pRoot = (BiTreeNode *)malloc(sizeof(BiTreeNode));
    BiTreeNode_Reset(tree->pRoot,,rootdata);
    //tree->pRoot->pLeftChild = 0;
    //tree->pRoot->pRightChild = 0;
    //tree->pRoot->pParent = 0;
    return true;
}
bool BinaryTreeDelete(BinaryTree *tree)
{
    if(tree->pRoot == NULL)
    {
        return false;
    }
    deleteNodeByNode(tree,tree->pRoot);
    return true;
}

bool IsTreeFull(BinaryTree *tree)
{
    if(tree->iSize >= tree->iMaxSize)
        return true;
    return false;
}

//search and statics
/*******************************************************/
/*******************************************************/
/**********************节点搜索*************************/
/*******************************************************/
/*******************************************************/
BiTreeNode* getNodeByIndex(BinaryTree *tree,int index)
{
    return BiTreeNode_NodeSearch(tree->pRoot,index);
}
/*******************************************************/
/*******************************************************/
/**********************叶子统计*************************/
/*******************************************************/
/*******************************************************/
int getLeaves(BinaryTree *tree)
{
    return NodeLeavesStatistics(tree->pRoot,);
}

/*******************************************************/
/*******************************************************/
/**********************高度统计*************************/
/*******************************************************/
/*******************************************************/
int getHeight(BinaryTree *tree)
{
    return NodeChildrenNodeHeigh(tree->pRoot);
}
/*******************************************************/
/*******************************************************/
/**********************宽度统计*************************/
/*******************************************************/
/*******************************************************/
int getWidth(BinaryTree *tree)
{
    int maxWidth=;                //save max width
    int parentWidth=;            //save this width
    int childrenWidth=;        //save next width
    BiTreeNode *tempNode = tree->pRoot;
    Queue *myQueue = (Queue*)malloc(sizeof(Queue));

    //create queue
    Queue_Create(myQueue,);

    if(tempNode -> pLeftChild != NULL)
    {
        Queue_push(myQueue,tempNode -> pLeftChild);
        parentWidth ++;
    }
    if(tempNode -> pRightChild != NULL)
    {
        Queue_push(myQueue,tempNode ->pRightChild);
        parentWidth ++;
    }

    while(!isQueueEmpty(myQueue))
    {
        while(parentWidth>)
        {
            tempNode = Queue_front(myQueue);
            Queue_pop(myQueue);
            if(tempNode -> pLeftChild != NULL)
            {
                Queue_push(myQueue , tempNode -> pLeftChild);
                childrenWidth ++;
            }
            if(tempNode -> pRightChild != NULL)
            {
                Queue_push(myQueue , tempNode -> pRightChild);
                childrenWidth ++;
            }
            parentWidth --;
        }
        parentWidth = childrenWidth;
        if(parentWidth > maxWidth)
        {
            maxWidth = parentWidth;
        }
        childrenWidth =;
    }

    Queue_Delete(myQueue);
    myQueue = NULL;

    return maxWidth;
}
/****************************************************************************************/
//name:      getTreeNowSize(BinaryTree *tree)
//describ:   You will get how much node that the tree has.
//called:
//input:     tree:tree address; index:new node
//output:    Number of nodes
/****************************************************************************************/
int getTreeNowSize(BinaryTree *tree)
{
    //quickly search
    //return tree->iSize;

    return NodeChildrenStatistics(tree->pRoot);
}
/****************************************************************************************/
//name:      getTreeNodeNumber(BinaryTree *tree)
//describ:   You will get the maximum capacity of the tree.
//called:
//input:     tree:tree address; index:new node
//output:    Tree capacity
/****************************************************************************************/
int getTreeMaxCapacity(BinaryTree *tree)
{
    return tree->iMaxSize;
}

//add/delete
/****************************************************************************************/
//name:      addLeftNodeByNode(BinaryTree *tree,int index,TreeElem data,BiTreeNode *pNode)
//describ:   adding a left child to pNode in tree.
//called:
//input:     tree:tree address; index:new node index; data:new node data; pNode:father node
//output:    true/false
/****************************************************************************************/
bool addLeftNodeByNode(BinaryTree *tree,int index,TreeElem data,BiTreeNode *pNode)    //添加左子树（使用父节点地址）
{
    BiTreeNode *pNodeCopy = pNode;//To make a copy of pNode  protect that is accidentally changed.
    BiTreeNode *newNode = NULL;
    if(IsTreeFull(tree))
    {
        return false ;
    }
    if(BiTreeNode_getLChild(pNodeCopy) == NULL)
    {
        newNode = (BiTreeNode *)malloc(sizeof(BiTreeNode));
        BiTreeNode_Reset(newNode,index,data);
        BiTreeNode_setLChild(pNodeCopy,newNode);
        BiTreeNode_setParenet(newNode,pNodeCopy);
    }
    else
    {
        return false ;
    }

    tree->iSize++;
    return true;
}
bool addRightNodeByNode(BinaryTree *tree,int index,TreeElem data,BiTreeNode *pNode)     //添加右子树（使用父节点地址）
{
    BiTreeNode *pNodeCopy = pNode;//To make a copy of pNode  protect that is accidentally changed.
    BiTreeNode *newNode = NULL;
    if(IsTreeFull(tree))
    {
        return false ;
    }
    if(BiTreeNode_getRChild(pNodeCopy) == NULL)
    {
        newNode = (BiTreeNode *)malloc(sizeof(BiTreeNode));
        BiTreeNode_Reset(newNode,index,data);
        BiTreeNode_setRChild(pNodeCopy,newNode);
        BiTreeNode_setParenet(newNode,pNodeCopy);
    }
    else
    {
        return false ;
    }

    tree->iSize++;
    return true;
}
bool addLeftNodeByIndex(BinaryTree *tree,int newIndex,TreeElem data,int searchIndex)//添加左子树（使用索引）
{
    BiTreeNode *tempNode;
    tempNode = getNodeByIndex(tree,searchIndex);//find the Node witch is index = searchIndex
    if(tempNode!=NULL)
    {
        return addLeftNodeByNode(tree,newIndex,data,tempNode);
    }
    return false;
}
bool addRightNodeByIndex(BinaryTree *tree,int newIndex,TreeElem data,int searchIndex)   //添加右子树（使用索引）
{
    BiTreeNode *tempNode;
    tempNode = getNodeByIndex(tree,searchIndex);//find the Node witch is index = searchIndex
    if(tempNode!=NULL)
    {
        return addRightNodeByNode(tree,newIndex,data,tempNode);
    }
    return false;
}
/****************************************************************************************/
//name:      deleteNodeByIndex(BinaryTree *tree,int index)
//describ:   to delete child tree by index
//called:
//input:     tree:tree address; index:new node index;
//output:    true/false
/****************************************************************************************/
bool deleteNodeByNode(BinaryTree *tree,BiTreeNode *pNode)                          //删除节点及其子节点（使用地址）
{
    BiTreeNode *parentNode = NULL;
    int nodeCNT;
    if(pNode != NULL && pNode != tree->pRoot)
    {
        /*Statistics*/
        nodeCNT=NodeChildrenStatistics(pNode);
        /*clear parent Node L/RChild*/
        parentNode= BiTreeNode_getParent(pNode);
        if(parentNode != NULL)
        {
            if(BiTreeNode_getLChild(parentNode) == pNode)
            {
                BiTreeNode_setLChild(parentNode,NULL);
            }
            else
            {
                BiTreeNode_setRChild(parentNode,NULL);
            }
        }

        /*Its all children and it will be deleted*/
        BiTreeNode_Delete(pNode);
        tree->iSize -=nodeCNT;
        return true;
    }
    return false;
}

bool deleteNodeByIndex(BinaryTree *tree,int index)                              //删除节点及其子节点（使用索引）
{
    BiTreeNode *deleteNode = getNodeByIndex(tree,index);
    if(deleteNode != NULL)
    {
        if(deleteNode == tree->pRoot)//rute can't not be delete
        {
            return false;
        }

        deleteNodeByNode(tree,deleteNode);
        return true;
    }
    return false;
}

//traversal
void PreorderTraversal(BinaryTree *tree)                                            //先序遍历
{
    printf("PreorderTraversal:\r\n");
    BiTreeNode_PreorderTraversal(tree->pRoot);
}

void InorderTraversal(BinaryTree *tree)                                                //中序遍历
{
    printf("InorderTraversal:\r\n");
    BiTreeNode_InorderTraversal(tree->pRoot);
}

void SubsequentTraversal(BinaryTree *tree)                                            //后序遍历
{
    printf("SubsequentTraversal:\r\n");
    BiTreeNode_SubsequentTraversal(tree->pRoot);
}

BinaryTree.h

#ifndef _BINARYTREE_H
#define _BINARYTREE_H
#include <stdlib.h>
#include "Mystdbool.h"
#include "Queue.h"
#include "BiTreeNode.h"
/*树定义*/
typedef struct binarytree
{
    BiTreeNode *pRoot;
    int iSize;
    int iMaxSize;
}BinaryTree;
//public
//create
bool BinaryTreeCreate(BinaryTree *tree,int size,int rootdata);
bool BinaryTreeDelete(BinaryTree *tree);
bool IsTreeFull(BinaryTree *tree);
//search and statistics
BiTreeNode* getNodeByIndex(BinaryTree *tree,int index);
int getLeaves(BinaryTree *tree);
int getHeight(BinaryTree *tree);
int getWidth(BinaryTree *tree);
int getTreeNowSize(BinaryTree *tree);
int getTreeMaxCapacity(BinaryTree *tree);
//add and delete
bool addLeftNodeByNode(BinaryTree *tree,int index,TreeElem data,BiTreeNode *pNode);    //添加左子树（使用父节点地址）
bool addRightNodeByNode(BinaryTree *tree,int index,TreeElem data,BiTreeNode *pNode);     //添加右子树（使用父节点地址）
bool addLeftNodeByIndex(BinaryTree *tree,int newIndex,TreeElem data,int searchIndex);    //添加左子树（使用索引）
bool addRightNodeByIndex(BinaryTree *tree,int newIndex,TreeElem data,int searchIndex);   //添加右子树（使用索引）
bool deleteNodeByNode(BinaryTree *tree,BiTreeNode *pNode);
bool deleteNodeByIndex(BinaryTree *tree,int index);
//traversal
void PreorderTraversal(BinaryTree *tree);                                            //先序遍历
void InorderTraversal(BinaryTree *tree)    ;                                            //中序遍历
void SubsequentTraversal(BinaryTree *tree);                                            //后序遍历

//private
bool IsTreeFull(BinaryTree *tree);
#endif

其他需要使用的关联文件

Queue.c:

#include <stdlib.h>
#include <stdio.h>
#include "Queue.h"

/*******************************************************/
/*******************************************************/
/**********************创建队列*************************/
/*******************************************************/
/*******************************************************/
bool Queue_Create(Queue *queue,int size)
{
    if(queue == NULL)
    {
        queue = malloc(sizeof(Queue));
    }

    queue->iSize = size;
    queue->iLength = ;
    queue->iTail=;
    queue->iHead=;
    queue->Datas = (ElemQueue *)malloc(size*sizeof(ElemQueue));
    return true;
}
/*******************************************************/
/*******************************************************/
/**********************删除队列*************************/
/*******************************************************/
/*******************************************************/
bool Queue_Delete(Queue *queue)
{
    free(queue->Datas);
    return true;
}
/*******************************************************/
/*******************************************************/
/*********************队头队尾操作**********************/
/*******************************************************/
/*******************************************************/
static void QueueTailAdd(Queue *queue)
{
    queue->iTail++;
    queue->iTail = queue->iTail % queue->iSize;
}
static void QueueHeadAdd(Queue *queue)
{
    queue->iHead ++;
    queue->iHead = queue->iHead % queue->iSize;
}
/*******************************************************/
/*******************************************************/
/***********************队列判空************************/
/*******************************************************/
/*******************************************************/
bool isQueueEmpty(Queue *queue)
{
    if(queue->iLength == )
    {
        return true;
    }
    return false;
}
/*******************************************************/
/*******************************************************/
/***********************队列判满************************/
/*******************************************************/
/*******************************************************/
bool isQueueFull(Queue *queue)
{
    if(queue->iLength>=queue->iSize)
    {
        return true;
    }
    return false;
}
/*******************************************************/
/*******************************************************/
/*******************返回队列现有长度********************/
/*******************************************************/
/*******************************************************/
int Queue_size(Queue *queue)
{
    return queue->iLength;
}
/*******************************************************/
/*******************************************************/
/********************往队尾放入元素*********************/
/*******************************************************/
/*******************************************************/
bool Queue_push(Queue *queue,ElemQueue data)
{
    if(isQueueFull(queue))
    {
        return ;
    }

    queue->Datas[queue->iTail] = data;
    QueueTailAdd(queue);
    queue->iLength++;
    return true;
}
/*******************************************************/
/*******************************************************/
/************获取队头第一个元素（不删除）***************/
/*******************************************************/
/*******************************************************/
ElemQueue Queue_front(Queue *queue)
{
    if(isQueueEmpty(queue))
    {
        return ;
    }

    return queue->Datas[queue->iHead];
}
ElemQueue Queue_back(Queue *queue)
{
    if(isQueueEmpty (queue))
    {
        return ;
    }
    return queue->Datas[queue->iTail];
}
/*******************************************************/
/*******************************************************/
/******************删除队列第一个元素*******************/
/*******************************************************/
/*******************************************************/
bool Queue_pop(Queue *queue)
{
    if(isQueueEmpty(queue))
    {
        return false;//queue empty
    }

    QueueHeadAdd(queue);
    queue->iLength--;
    return true;
}
/*******************************************************/
/*******************************************************/
/*****************打印队列中的全部元素******************/
/*******************************************************/
/*******************************************************/
void Queue_printf(Queue *queue)
{
    int i;
    int temp = queue->iHead;
    printf("queue datas:\r\n");
    for(i=;i<queue->iLength;i++)
    {
        printf("%d ",queue->Datas[temp++%queue->iSize]);
    }

}

Queue.h:

#ifndef _QUEUE_H
#define _QUEUE_H
#include "BinaryTree.h"
#include "Mystdbool.h"

typedef  struct bitreenode *ElemQueue;
//#define ElemQueue struct bitreenode*

typedef struct circlequeue
{
    int iLength;
    int iSize;
    int iHead;
    int iTail;
    ElemQueue (*Datas);
}Queue;

bool Queue_Create(Queue *queue,int size);
bool Queue_Delete(Queue *queue);
bool isQueueEmpty(Queue *queue);
bool isQueueFull(Queue *queue);
int Queue_size(Queue *queue);
bool Queue_push(Queue *queue,ElemQueue data);
ElemQueue Queue_front(Queue *queue);
ElemQueue Queue_back(Queue *queue);
bool Queue_pop(Queue *queue);
void Queue_printf(Queue *queue);

#endif

Mystdbool.h(用于声明bool)

#ifndef __MYSTDBOOL_H
#define __MYSTDBOOL_H

typedef enum Bool
{
    false=,
    true,
}bool;

#endif

main.c(用于测试)

#include <stdlib.h>
#include <stdio.h>
#include "BinaryTree.h"

int main(void)
{
    BinaryTree tree={};
    BinaryTreeCreate(&tree,,);
    //first level
    addLeftNodeByIndex(&tree,,,);
    addRightNodeByIndex(&tree,,,);
    //second level
    addLeftNodeByIndex(&tree,,,);
    addRightNodeByIndex(&tree,,,);
    addLeftNodeByIndex(&tree,,,);
    addRightNodeByIndex(&tree,,,);

    PreorderTraversal(&tree);
    InorderTraversal(&tree);
    SubsequentTraversal(&tree);

    printf("leaves:%d\r\n",getLeaves(&tree));
    printf("height:%d\r\n",getHeight(&tree));
    printf("width:%d\r\n",getWidth(&tree));
    printf("Nodes:%d\r\n",getTreeNowSize(&tree));

    system("pause");
    return ;
}

运行结果：

---

---

---

---

C++版本

程序源码

本程序包含三部分

BinaryTree.h中为树的操作

BinaryTreeNode.h中为节点的操作

main.c中程序用于测试

BiTreeNode.h:

#ifndef _BITREENODE_H
#define _BITREENODE_H
#include<iostream>
using namespace std;

template <typename T>
class BiTreeNode
{
public:
    BiTreeNode();
    BiTreeNode(int index,T data);
    virtual ~BiTreeNode();
    //get data
    int getIndex();
    T getData();
    BiTreeNode *getParent();
    BiTreeNode *getLChild();
    BiTreeNode *getRChild();
    BiTreeNode *getInorderPrecursor();                    //获取中序前驱
    BiTreeNode *getInorderSubsequence();                //获取中序后继
    //set data
    void setIndex(int index);
    void setData(T data);
    void setParenet(BiTreeNode *Node);
    void setLChild(BiTreeNode *Node);
    void setRChild(BiTreeNode *Node);
    //else
    BiTreeNode *NodeSearch(int index);                    //通过索引搜索节点（以本节点作为根寻找树的某个节点）
    int NodeLeavesStatistics(int leaves = );            //统计叶子数
    int NodeChildrenNodeHeigh();                        //统计子节点的最大高度（包含本节点）/（以本节点作为根求树的高度）
    int NodeChildrenStatistics();                        //统计子节点数(包含本节点)
    int NodeDelete();                                    //删除节点
    //traversal
    void NodePreorderTraversal();
    void NodeInorderTraversal();
    void NodeSubsequentTraversal();

private:
    int m_iIndex;
    T m_tData;
    BiTreeNode *m_pParent;
    BiTreeNode *m_pLeftChild;
    BiTreeNode *m_pRightChild;

    //struct NodeWidth<T> stNodeWidth;
};

template <typename T>
BiTreeNode<T>::BiTreeNode()
{
    m_iIndex = ;
    m_tData = ;
    m_pParent = NULL;
    m_pLeftChild = NULL;
    m_pRightChild = NULL;
}

template <typename T>
BiTreeNode<T>::BiTreeNode(int index,T data)
{
    m_iIndex = index;
    m_tData = data;
    m_pParent = NULL;
    m_pLeftChild = NULL;
    m_pRightChild = NULL;
}

template <typename T>
BiTreeNode<T>::~BiTreeNode()
{
    if(m_pLeftChild != NULL)
    {
        m_pLeftChild->NodeDelete();
        m_pLeftChild = NULL;
    }
    if(m_pRightChild != NULL)
    {
        m_pRightChild->NodeDelete();
        m_pRightChild = NULL;
    }
    m_pParent = NULL;
}
/*-----------------------getdata------------------------*/
template <typename T>
int BiTreeNode<T>::getIndex()
{
    return m_iIndex;
}

template <typename T>
T BiTreeNode<T>::getData()
{
    return m_tData;
}

template <typename T>
BiTreeNode<T> *BiTreeNode<T>::getParent()
{
    return m_pParent;
}

template <typename T>
BiTreeNode<T> *BiTreeNode<T>::getLChild()
{
    return m_pLeftChild;
}

template <typename T>
BiTreeNode<T> *BiTreeNode<T>::getRChild()
{
    return m_pRightChild;
}

template <typename T>
BiTreeNode<T> *BiTreeNode<T>::getInorderPrecursor()
{
    /*
        condition 1: Node has left child.
        condition 2: Node hasn't left child,and it is its father right child.
        condition 3: Node hasn't left child,and it is its father left child.
    */
    /*condition 1:node has left child*/
    if(NULL != this->getLChild())
    {
        BiTreeNode *tempNode=this->getLChild();
        while(NULL != tempNode->getRChild() )
        {
            tempNode=tempNode->getRChild();
        }
        return  tempNode;
    }
    else
    {
        BiTreeNode *fatherNode=this->getParent();
        if(NULL == fatherNode)
        {
            return NULL;//it is root.
        }
        /*condition 2*/
        else if(fatherNode->getRChild() == this)
        {
            return fatherNode;
        }
        /*condition*/
        else
        {
            while( fatherNode->getParent()->getRChild() != fatherNode)
            {
                fatherNode =fatherNode ->getParent();
                if(NULL == fatherNode )
                {
                    return NULL;//it is root;
                }
            }
            return fatherNode->getParent();
        }
    }
    return NULL;
}

template <typename T>
BiTreeNode<T> *BiTreeNode<T>::getInorderSubsequence()                //获取中序后继
{
    /*
        condition 1: Node has right child.
        condition 2: Node hasn't right child,and it is its father left child.
        condition 3: Node hasn't right child,and it is its father right child.
    */
    /*condition 1*/
    if(NULL != this->getRChild())
    {
        BiTreeNode *tempNode = this->getRChild();
        while(NULL != tempNode->getLChild() )
        {
            tempNode=tempNode->getLChild();
        }
        return  tempNode;
    }
    /*condition 2*/
    else
    {
        BiTreeNode *fatherNode=this->getParent();
        if(NULL == fatherNode)//it is root.
        {
            return NULL;
        }
        else if(fatherNode->getLChild() == this)
        {
            return fatherNode;
        }
        else
        {
            while(fatherNode->getParent()->getLChild() !=fatherNode)
            {
                fatherNode=fatherNode->getParent();
                if(NULL == fatherNode)
                {
                    return NULL;//it is root;
                }
            }
            return fatherNode->getParent();
        }
    }
}
/*-----------------------setdata------------------------*/
template <typename T>
void BiTreeNode<T>::setIndex(int index)
{
    m_iIndex = index;
}
template <typename T>
void BiTreeNode<T>::setData(T data)
{
    m_tData = data;
}
template <typename T>
void BiTreeNode<T>::setParenet(BiTreeNode *Node)
{
    m_pParent = Node;
}

template <typename T>
void BiTreeNode<T>::setLChild(BiTreeNode *Node)
{
    m_pLeftChild = Node;
}

template <typename T>
void BiTreeNode<T>::setRChild(BiTreeNode *Node)
{
    m_pRightChild = Node;
}

/*-----------------------else------------------------*/
template <typename T>
BiTreeNode<T> *BiTreeNode<T>::NodeSearch(int index)
{
    BiTreeNode<T> *tempNode = NULL;
    if(m_iIndex == index)
    {
        return this;
    }
    if(m_pLeftChild != NULL)
    {
        tempNode = m_pLeftChild->NodeSearch(index);
        if(tempNode != NULL)//match
        {
            return tempNode;
        }
    }

    if(m_pRightChild !=NULL)
    {
        tempNode = m_pRightChild->NodeSearch(index);
        if(tempNode != NULL)// match
        {
            return tempNode;
        }
    }

    return NULL;
}

/*statistcal children node heigh(includding me)*/
template <typename T>
int BiTreeNode<T>::NodeChildrenNodeHeigh()
{
    int heightLeft = ;
    int heightRight =;
    if(m_pLeftChild != NULL)
    {
        heightLeft += m_pLeftChild->NodeChildrenNodeHeigh();
    }
    if(m_pRightChild != NULL)
    {
        heightRight += m_pRightChild->NodeChildrenNodeHeigh();
    }
    if(heightRight > heightLeft)
    {
        return ++heightRight;
    }
    else
    {
        return ++heightLeft;
    }
}

/*statistcal leaves node(includding me)*/
template <typename T>
int BiTreeNode<T>::NodeLeavesStatistics(int leaves)
{
    if(this->m_pLeftChild != NULL)
    {
        leaves = this->m_pLeftChild->NodeLeavesStatistics(leaves);
    }
    if(this->m_pRightChild != NULL)
    {
        leaves = this->m_pRightChild->NodeLeavesStatistics(leaves);
    }
    if(this->getLChild() == NULL && this->getRChild() == NULL)
    {
        leaves ++;
    }
    return leaves;
}
/*statistcal children node(includding me)*/
template <typename T>
int BiTreeNode<T>::NodeChildrenStatistics()
{
    int iCnt=;
    if(this->m_pLeftChild != NULL)
    {
        iCnt+=this->m_pLeftChild->NodeChildrenStatistics();
    }
    if(this->m_pRightChild!= NULL)
    {
        iCnt+=this->m_pRightChild->NodeChildrenStatistics();
    }
    iCnt++;
    return iCnt;
}

template <typename T>
int  BiTreeNode<T>::NodeDelete()
{
    int Times=;
    if(this->m_pLeftChild != NULL)
    {
         //delete this->getLChild();
        Times+=this->m_pLeftChild->NodeDelete();
        this->m_pLeftChild =NULL;
    }
    if(this->m_pRightChild!= NULL)
    {
        //delete this->getRChild();
        Times+=this->m_pRightChild->NodeDelete();
        this->m_pRightChild =NULL;
    }
    Times++;
    delete this;
    return Times;
}
/*-----------------------traversal------------------------*/
template <typename T>
void BiTreeNode<T>::NodePreorderTraversal()
{
    cout<<"Index:"<<this->getIndex()<<";Data:"<<this->getData()<<endl;

    if(this->getLChild() != NULL)
    {
        this->getLChild()->NodePreorderTraversal();
    }

    if(this->getRChild() != NULL)
    {
        this->getRChild()->NodePreorderTraversal();
    }
}

template <typename T>
void BiTreeNode<T>::NodeInorderTraversal()
{
    if(this->getLChild() != NULL)
    {
        this->getLChild()->NodeInorderTraversal();
    }

    cout<<"Index:"<<this->getIndex()<<";Data:"<<this->getData()<<endl;

    if(this->getRChild() != NULL)
    {
        this->getRChild()->NodeInorderTraversal();
    }
}

template <typename T>
void BiTreeNode<T>::NodeSubsequentTraversal()
{
    if(this->getLChild() != NULL)
    {
        this->getLChild()->NodeSubsequentTraversal();
    }

    if(this->getRChild() != NULL)
    {
        this->getRChild()->NodeSubsequentTraversal();
    }

    cout<<"Index:"<<this->getIndex()<<";Data:"<<this->getData()<<endl;
}

#endif

BinaryTree.h

#ifndef _BINARYTREE_H
#define _BINARYTREE_H

#include <iostream>
#include <queue>
#include "BiTreeNode.h"
using namespace std;

template <typename T>
class BinaryTree
{
public:
    BinaryTree(int size,int index,T data);
    BinaryTree(int size);
    virtual ~BinaryTree();
    bool IsTreeEmpty();                                                //树是否为空
    bool IsTreeFull();                                                //树的容量是否已满
    //search
    BiTreeNode<T> *getNodeByIndex(int index);                        //通过索引搜索节点
    int getLeaves();                                                //获取树的叶子数
    int getHeight();                                                //获取树的高度(包含根节点)
    int getWidth();                                                    //获取树的宽度(包含根节点)
    int getNowSize();                                                //获取树现在的节点数（包含根节点）
    int getMaxSize();                                                //获取树的最大节点数
    //add/delete
    bool addLeftNodeByIndex(int newIndex,T data,int searchIndex);    //添加左子树（使用索引）
    bool addRightNodeByIndex(int newIndex,T data,int searchIndex);  //添加右子树（使用索引）
    bool addLeftNodeByNode(int index,T data,BiTreeNode<T> *pNode);  //添加左子树（使用节点地址）
    bool addRightNodeByNode(int index,T data,BiTreeNode<T> *pNode); //添加右子树（使用节点地址）

    virtual bool deleteNodeByIndex(int index);                        //删除节点（使用索引）
    virtual bool deleteNodeByNode(BiTreeNode<T> *pNode);            //删除节点（使用地址）

    //traversal
    void PreorderTraversal();                                        //先序遍历
    void InorderTraversal();                                        //中序遍历
    void SubsequentTraversal();                                        //后序遍历

protected:
    BiTreeNode<T> *m_pRoot;                                            //tree root
    int m_iSize;                                                    //Tree now nodes size (without root)
    int m_iMaxSize;                                                    //Tree max nodes size (without root)
};

template <typename T>
BinaryTree<T>::BinaryTree(int size,int index,T data)
{
    m_pRoot = new BiTreeNode<T>(index,data);
    m_pRoot->setLChild(NULL);
    m_pRoot->setRChild(NULL);
    m_pRoot->setParenet(NULL);
    m_iSize = ;
    m_iMaxSize = size;
}

template <typename T>
BinaryTree<T>::BinaryTree(int size)
{
    m_pRoot = new BiTreeNode<T>(,);
    m_pRoot->setLChild(NULL);
    m_pRoot->setRChild(NULL);
    m_pRoot->setParenet(NULL);
    m_iSize = ;
    m_iMaxSize = size;
}

template <typename T>
BinaryTree<T>::~BinaryTree()
{
    if(NULL != m_pRoot)
        delete m_pRoot;
    m_pRoot=NULL;
}

template <typename T>
bool BinaryTree<T>::IsTreeEmpty()
{
    if(m_iSize == )
        return true;
    return false;
}

template <typename T>
bool BinaryTree<T>::IsTreeFull()
{
    if(m_iSize >= m_iMaxSize)
        return true;
    return false;
}

//search
template <typename T>
BiTreeNode<T> *BinaryTree<T>::getNodeByIndex(int index)
{
    if(NULL == m_pRoot)
    {
        return NULL;
    }
    return m_pRoot->NodeSearch(index);
}

template <typename T>
int BinaryTree<T>::getLeaves()
{
    if(NULL == m_pRoot)
    {
        return ;
    }
    return m_pRoot->NodeLeavesStatistics();
}

template <typename T>
int BinaryTree<T>::getWidth()
{
    if(NULL == m_pRoot)
    {
        return ;
    }
    int maxWidth=;                //save max width
    int parentWidth=;            //save this width
    int childrenWidth=;        //save next width
    queue<BiTreeNode<T>*> stdQueue;
    BiTreeNode<T> *tempNode = m_pRoot;
    if(tempNode -> getLChild() != NULL)
    {
        stdQueue.push(tempNode -> getLChild());
        parentWidth ++;
    }
    if(tempNode -> getRChild() != NULL)
    {
        stdQueue.push(tempNode ->getRChild());
        parentWidth ++;
    }

    while(!stdQueue.empty())
    {
        while(parentWidth>)
        {
            tempNode = stdQueue.front();
            stdQueue.pop();
            if(tempNode -> getLChild() != NULL)
            {
                stdQueue.push(tempNode -> getLChild());
                childrenWidth ++;
            }
            if(tempNode -> getRChild() != NULL)
            {
                stdQueue.push(tempNode ->getRChild());
                childrenWidth ++;
            }
            parentWidth --;
        }
        parentWidth = childrenWidth;
        if(parentWidth > maxWidth)
        {
            maxWidth = parentWidth;
        }
        childrenWidth =;
    }

//    result =  m_pRoot->NodeChildrenNodeWidth(&child);
    return maxWidth;
}

template <typename T>
int BinaryTree<T>::getHeight()
{
    if(NULL == m_pRoot)
        return ;
    return m_pRoot->NodeChildrenNodeHeigh();//including root
}

template <typename T>
int BinaryTree<T>::getNowSize()
{
    if(NULL == m_pRoot)
    {
        return ;
    }
    //return m_iSize;//quickly get Size
    return m_pRoot ->NodeChildrenStatistics();//including root
}

template <typename T>
int BinaryTree<T>::getMaxSize()
{
    return m_iMaxSize ;
}

//add/delete
template <typename T>
bool BinaryTree<T>::addLeftNodeByIndex(int newIndex,T data,int searchIndex)
{
    if(NULL == m_pRoot)
    {
        return false;
    }
    BiTreeNode<T> *tempNode;
    tempNode = m_pRoot->NodeSearch(searchIndex);//find the node that index  is = searchIndex
    if(tempNode!=NULL)
    {
        return addLeftNodeByNode(newIndex,data,tempNode);
    }
    return false;
}
template <typename T>
bool BinaryTree<T>::addRightNodeByIndex(int newIndex,T data,int searchIndex)
{
    if(NULL == m_pRoot)
    {
        return false;
    }
    BiTreeNode<T> *tempNode ;
    tempNode = m_pRoot->NodeSearch(searchIndex);
    if(tempNode!=NULL)
    {
        return addRightNodeByNode(newIndex,data,tempNode);
    }
    return false;
}
template <typename T>
bool BinaryTree<T>::addLeftNodeByNode(int index,T data,BiTreeNode<T> *pNode)
{
    BiTreeNode<T> *pNodeCopy = pNode;//make a copy of pNode to protect the pNode being changed by accidentally
    if(IsTreeFull())
    {
        return false ;
    }
    if(pNodeCopy -> getLChild() == NULL)
    {
        BiTreeNode<T> *newNode = new BiTreeNode<T>(index,data);
        pNodeCopy->setLChild(newNode);
        newNode->setParenet(pNodeCopy);
    }
    else
    {
        return false ;
    }

    m_iSize++;
    return true;
}

template <typename T>
bool BinaryTree<T>::addRightNodeByNode(int index,T data,BiTreeNode<T> *pNode)
{
    BiTreeNode<T> *pNodeCopy = pNode;//make a copy of pNode to protect the pNode being changed by accidentally
    if(IsTreeFull())
    {
        return false ;
    }
    if(pNodeCopy -> getRChild() == NULL)
    {
        BiTreeNode<T> *newNode = new BiTreeNode<T>(index,data);
        pNodeCopy->setRChild(newNode);
        newNode->setParenet(pNodeCopy);
    }
    else
    {
        return false ;
    }

    m_iSize++;
    return true;
}

template <typename T>
bool BinaryTree<T>::deleteNodeByIndex(int index)
{
    if(IsTreeEmpty())
    {
        return false;
    }

    BiTreeNode<T> *deleteNode = m_pRoot->NodeSearch(index);
    if(deleteNode != NULL)
    {
        if(deleteNode == m_pRoot)
        {
            cout<<"BinaryTree<T>::deleteNodeByIndex():"<<index<<"是根节点不能删除"<<endl;
            return false;
        }
        return deleteNodeByNode(deleteNode);
    }
    return false;
}
template <typename T>
bool BinaryTree<T>::deleteNodeByNode(BiTreeNode<T> *pNode)
{
    if(IsTreeEmpty())
        return false;

    if(pNode!=NULL)
    {
        /*clear parent Node L/RChild*/
        BiTreeNode<T> *parentNode = pNode->getParent();
        if(parentNode != NULL)
        {
            if(parentNode->getLChild() == pNode)
            {
                parentNode->setLChild(NULL);
            }
            else
            {
                parentNode->setRChild(NULL);
            }
        }
        /*delete node*/
        int SizeDec;//use to caculate how much Node was delete
        SizeDec = pNode->NodeDelete();
        m_iSize-=SizeDec;
        return true;
    }
    return false;
}

//traversal
template <typename T>
void BinaryTree<T>::PreorderTraversal()
{
    cout<<"PerorderTraversal:"<<endl;
    if(NULL == m_pRoot)
    {
        return ;
    }
    m_pRoot ->NodePreorderTraversal();
}
template <typename T>
void BinaryTree<T>::InorderTraversal()
{
    cout<<"InorderTraversal:"<<endl;
    if(NULL == m_pRoot)
    {
        return ;
    }
    m_pRoot ->NodeInorderTraversal();
}
template <typename T>
void BinaryTree<T>::SubsequentTraversal()
{
    cout<<"SubsequentTraversal:"<<endl;
    if(NULL == m_pRoot)
    {
        return ;
    }
    m_pRoot ->NodeSubsequentTraversal();
}

#endif 

main.c(本部分用于测试)

#include <iostream>
#include <vector>
#include "BinaryTree.h"
#include "BinarySearchTree.h"

using namespace std;

int main()
{
    BinaryTree<int> *tree = new BinaryTree<int>(,,);
    tree->addLeftNodeByIndex(,,);
    tree->addRightNodeByIndex(,,);
    tree->addLeftNodeByIndex(,,);
    tree->addRightNodeByIndex(,,);
    tree->addLeftNodeByIndex(,,);
    tree->addRightNodeByIndex(,,);
    //preorderTraversal()/InorderTraversal()/SubsequentTraversal() check
    tree->PreorderTraversal();
    //tree->InorderTraversal();
    //tree->SubsequentTraversal();

    //getNowSize() check
    cout<<"tree size(except root):"<<tree->getNowSize()<<endl;

    //getLeaves() check;
    cout<<"tree leaves:"<<tree->getLeaves()<<endl;

    //getHeight() check;
    cout<<"getHeight():"<<tree->getHeight()<<endl;

    //getWidth() check;
    cout<<"getWidth():"<<tree->getWidth()<<endl;

    //deleteNodeByIndex() check
    tree->deleteNodeByIndex();
    tree->PreorderTraversal();

    system("pause");
    return ;
}

测试结果：

程序详解

以下介绍几点

1. 树的基本结构
2. 构建树
3. 添加左/右节点
4. 统计叶子
5. 统计高度
6. 统计宽度

---

一、数的基本结构

　　树由两部分构成，结点类（BiTreeNode.h）和树的本体（BinaryTree.h）

　　节点类中的内容用于储存数据，树的本体中将这些节点连接起来。

　　节点的主要成员：

1. 　　节点索引号m_iIndex：用于标记节点号码，如图红色的数字
2. 　　节点数据m_tData： 用于标记节点数字，如图黑色数字
3. 　　节点的父节点指针*m_pParent：通过该指针可以找到在树中该节点的父亲
4. 　　节点的左子节点指针*m_pLeftChild：通过该指针可以找到在树中该节点的左孩子
5. 　　节点的右子节点指针*m_pRightChild：通过该指针可以找到树中该节点的右孩子

private:
    int m_iIndex;
    T m_tData;
    BiTreeNode *m_pParent;
    BiTreeNode *m_pLeftChild;
    BiTreeNode *m_pRightChild;

　　二叉树的主要成员：

1. 　　树根指针*m_pRoot：该指针指向树的根节点
2. 　　树的现有节点数m_iSize：指示现在树的节点
3. 　　树的最大节点树m_iMaxSize：指示这棵树最大可以存放多少节点

protected:
    BiTreeNode<T> *m_pRoot;                                            //tree root
    int m_iSize;                                                    //Tree now nodes size (without root)
    int m_iMaxSize;    

二、构建树:BinaryTree构造函数

1. 创建根节点
2. 设置根节点的父母和左右孩子为空
3. 设置树的大小为1，最大节点数为size。

template <typename T>
BinaryTree<T>::BinaryTree(int size,int index,T data)
{
    m_pRoot = new BiTreeNode<T>(index,data);
    m_pRoot->setLChild(NULL);
    m_pRoot->setRChild(NULL);
    m_pRoot->setParenet(NULL);
    m_iSize = ;
    m_iMaxSize = size;
}

三、添加左(右)节点addLeftNodeByNode()/addLeftNodeByIndex()

方法一、在目标节点后面添加新节点addLeftNodeByNode()

1. 树没有空间则不能添加，返回失败。
2. 如果目标节点的左子为空，使用（index，data）创建一个新的节点，并把该节点挂在目标节点后

template <typename T>
bool BinaryTree<T>::addLeftNodeByNode(int index,T data,BiTreeNode<T> *pNode)
{
    BiTreeNode<T> *pNodeCopy = pNode;//make a copy of pNode to protect the pNode being changed by accidentally
    if(IsTreeFull())
    {
        return false ;
    }
    if(pNodeCopy -> getLChild() == NULL)
    {
        BiTreeNode<T> *newNode = new BiTreeNode<T>(index,data);
        pNodeCopy->setLChild(newNode);
        newNode->setParenet(pNodeCopy);
    }
    else
    {
        return false ;
    }

    m_iSize++;
    return true;
}

方法二、通过索引添加新节点addLeftNodeByIndex()

1. 使用节点中Node_Search()方法从根节点开始查找索引为searchIndex的节点，找到并取出目标节点的指针
2. 使用方法一为目标节点添加左节点

template <typename T>
bool BinaryTree<T>::addLeftNodeByIndex(int newIndex,T data,int searchIndex)
{
    if(NULL == m_pRoot)
    {
        return false;
    }
    BiTreeNode<T> *tempNode;
    tempNode = m_pRoot->NodeSearch(searchIndex);//find the node that index  is = searchIndex
    if(tempNode!=NULL)
    {
        return addLeftNodeByNode(newIndex,data,tempNode);
    }
    return false;
}

四、统计叶子

从树根开始往下搜索，如果一个节点的没有左右子节点，那么它为叶子。在节点类中递归实现

template <typename T>
int BinaryTree<T>::getLeaves()
{
    if(NULL == m_pRoot)
    {
        return ;
    }
    return m_pRoot->NodeLeavesStatistics();
}

template <typename T>
int BiTreeNode<T>::NodeLeavesStatistics(int leaves)
{
    if(this->m_pLeftChild != NULL)
    {
        leaves = this->m_pLeftChild->NodeLeavesStatistics(leaves);
    }
    if(this->m_pRightChild != NULL)
    {
        leaves = this->m_pRightChild->NodeLeavesStatistics(leaves);
    }
    if(this->getLChild() == NULL && this->getRChild() == NULL)
    {
        leaves ++;
    }
    return leaves;
}

五、统计高度

从树根开始一直往下搜索。直到找到了叶子（无左右孩子）。在节点类中递归实现

template <typename T>
int BinaryTree<T>::getHeight()
{
    if(NULL == m_pRoot)
        return ;
    return m_pRoot->NodeChildrenNodeHeigh();//including root
}

template <typename T>
int BiTreeNode<T>::NodeChildrenNodeHeigh()
{
    int heightLeft = ;
    int heightRight =;
    if(m_pLeftChild != NULL)
    {
        heightLeft += m_pLeftChild->NodeChildrenNodeHeigh();
    }
    if(m_pRightChild != NULL)
    {
        heightRight += m_pRightChild->NodeChildrenNodeHeigh();
    }
    if(heightRight > heightLeft)
    {
        return ++heightRight;
    }
    else
    {
        return ++heightLeft;
    }
}

六、统计宽度

如图所示，这棵树第一层宽度为1，第二层宽度为2，第三层宽度为4，所以这棵树的最大宽度为4

综上所述我们需要统计最节点数最多的一层有几个节点，所以我们按层统计

1. 创建一个队列stdQueue存放节点，一个parentWidth用于储存上一层的宽度,一个childrenWidth用于储存下一层的宽度，以及一个maxWidth用于储存出现过的最大宽度。
2. 把根节点的两个孩子（黑色9和黑色6）加入队列中,每加一个parentWidth+1，这时队列中有两个元素，parentWidth等于2。此时队列中有两个元素（6,8）,parentWidth=2;childrenWidth=0;maxWidth=2
3. 从队列中取出第一个元素（9），parentWidth-1，此时parentWidth=1，他有两个孩子（黑色8黑色7）加入队列中,childrenWidth+=2。此时队列中有三个元素（6,8,7）,parentWidth=1;childrenWidth=2
4. 同上，从队列中取出第一个元素（6），parentWidth-1，此时parentWidth=0，他的两个孩子（黑5和黑4）加入队列中，childrenWidth+=2。此时队列中有四个元素（8,7,5,4）,parentWidth=0;childrenWidth=4
5. 由于parentWidth=0了，所以本层统计完成，让parentWidth=childrenWidth开始统计下一层。此时队列中有四个元素（8,7,5,4）,parentWidth=4;childrenWidth=0；maxWidth=4;
6. 同第3、4步，取出队列中第一个元素(8),它没有孩子，取出队列中第二个元素(7),它没有孩子...直到队列元素取出完毕，因为他们都没有子节点，所以队列为空，就是统计完成的条件。maxWidth=4;

template <typename T>
int BinaryTree<T>::getWidth()
{
    if(NULL == m_pRoot)
    {
        return ;
    }
    int maxWidth=;                //save max width
    int parentWidth=;            //save this width
    int childrenWidth=;        //save next width
    queue<BiTreeNode<T>*> stdQueue;
    BiTreeNode<T> *tempNode = m_pRoot;
    if(tempNode -> getLChild() != NULL)
    {
        stdQueue.push(tempNode -> getLChild());
        parentWidth ++;
    }
    if(tempNode -> getRChild() != NULL)
    {
        stdQueue.push(tempNode ->getRChild());
        parentWidth ++;
    }

    while(!stdQueue.empty())
    {
        while(parentWidth>)
        {
            tempNode = stdQueue.front();
            stdQueue.pop();
            if(tempNode -> getLChild() != NULL)
            {
                stdQueue.push(tempNode -> getLChild());
                childrenWidth ++;
            }
            if(tempNode -> getRChild() != NULL)
            {
                stdQueue.push(tempNode ->getRChild());
                childrenWidth ++;
            }
            parentWidth --;
        }
        parentWidth = childrenWidth;
        if(parentWidth > maxWidth)
        {
            maxWidth = parentWidth;
        }
        childrenWidth =;
    }

//    result =  m_pRoot->NodeChildrenNodeWidth(&child);
    return maxWidth;
}