数学图形(1.40)T_parameter
不记得在哪搞了个数学公式生成的图形.
vertices = t = from to (*PI)
r = 2.0
x = r*(*cos(t) - cos(*t))
y = r*(*sin(t) - sin(*t))
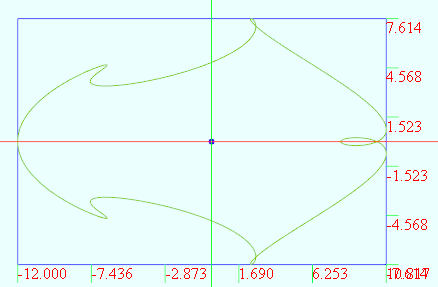
给线加上一维变量的变化,使之变成面:
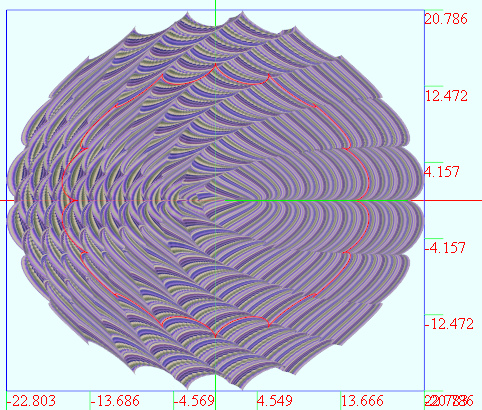
vertices = D1: D2: u = from to (*PI) D1
v = from to D2 x = (v+)*cos(u) - cos((v+)*u)
y = v*sin(u) - sin((v+)*u)
数学图形(1.40)T_parameter的更多相关文章
- WHY数学图形可视化工具(开源)
WHY数学图形可视化工具 软件下载地址:http://files.cnblogs.com/WhyEngine/WhyMathGraph.zip 源码下载地址: http://pan.baidu.com ...
- 数学图形(1.49)Nephroid曲线
昨天IPhone6在国内发售了,我就顺手发布个关于肾的图形.Nephroid中文意思是肾形的.但是这种曲线它看上去却不像个肾,当你看到它时,你觉得它像什么就是什么吧. The name nephroi ...
- 数学图形(1.48)Cranioid curve头颅线
这是一种形似乎头颅的曲线.这种曲线让我想起读研的时候,搞的医学图像三维可视化.那时的原始数据为脑部CT图像.而三维重建中有一种方式是面绘制,是将每一幅CT的颅骨轮廓提取出来,然后一层层地罗列在一起,生 ...
- 数学图形之贝塞尔(Bézier)曲面
前面章节中讲了贝塞尔(Bézier)曲线,而贝塞尔曲面是对其多一个维度的扩展.其公式依然是曲线的公式: . 而之所以由曲线变成曲面,是将顶点横向连了再纵向连. 很多计算机图形学的教程都会有贝塞尔曲面的 ...
- 数学图形(1.47)贝塞尔(Bézier)曲线
贝塞尔曲线又称贝兹曲线或贝济埃曲线,是由法国数学家Pierre Bézier所发现,由此为计算机矢量图形学奠定了基础.它的主要意义在于无论是直线或曲线都能在数学上予以描述. 上一节讲的是高次方程曲线, ...
- 数学图形之Breather surface
这是一种挺漂亮的曲面图形,可惜没有找到太多的相关解释. In differential equations, a breather surface is a mathematical surface ...
- 数学图形之Kuen Surface
Kuen Surface应该又是一个以数学家名字命名的曲面.本文将展示几种Kuen Surface的生成算法和切图,其中有的是标准的,有的只是相似.使用自己定义语法的脚本代码生成数学图形.相关软件参见 ...
- 数学图形之Boy surface
这是一个姓Boy的人发现的,所以取名为Boy surface.该图形与罗马图形有点相似,都是三分的图形.它甚至可以说是由罗马曲面变化而成的. 本文将展示几种Boy曲面的生成算法和切图,使用自己定义语法 ...
- 数学图形之SineSurface与粽子曲面
SineSurface直译为正弦曲面.这有可能和你想象的正弦曲线不一样.如果把正弦曲线绕Y轴旋转,得到的该是正弦波曲面.这个曲面与上一节中的罗马曲面有些相似,那个是被捏过的正四面体,这个则是个被捏过正 ...
随机推荐
- ASP.NET Zero--4.不使用谷歌字体,提升加载速度
jtable控件样式中会使用到谷歌字体,每次访问都特别慢 1.打开jtable.css文件 [..\MyCompanyName.AbpZeroTemplate.Web\libs\jquery-jtab ...
- js的浮点(小数)数+-*/
//除法 function accDiv(arg1,arg2){ var t1=0,t2=0,r1,r2; try{t1=arg1.toString().split(".")[1] ...
- Python爬虫-request的用法
import requests if __name__ == '__main__': #基本用法 #response = requests.get("http://httpbin.org/g ...
- 烈焰遮天 cocos 手游mmo 源码 解析
引擎: cocos2.x 代码: c++ 混合 lua 游戏类型: mmo 工程结构: game : 游戏启动地方 gamelogic:接sdk相关,登陆支付统计等 libFramework:主要本游 ...
- BNUOJ 52517 Another Server
网络流. 似乎有别的做法,没想. #include<bits/stdc++.h> using namespace std; + ; const int INF = 0x7FFFFFFF; ...
- Linux 下安装gmpy2
GMP(GNU Multiple Precision Arithmetic Library,即GNU高精度算术运算库),它是一个开源的高精度运算库,其中不但有普通的整数.实数.浮点数的高精度运算,还有 ...
- javascript入门教程笔记
BOM BOM 是“ Browser Object Model ”的缩写,简称“ 浏览器对象模型 ”. BOM 定义了 JavaScript 操作浏览器的接口,提供了访问某些功能(如浏览器窗口大小.版 ...
- margin padding 图
- 【二分答案】BZOJ2016-Chocolate Eating
[题目大意] n块巧克力,每次吃可以增加ai点快乐,每天早晨睡觉起来快乐值会减半,求如何使d天睡觉前的最小快乐值最大. [思路] 二分每天的最小快乐值,只要没有达到快乐值就继续吃. 不知道为什么了WA ...
- bzoj 1579: [Usaco2009 Feb]Revamping Trails 道路升级 -- 分层图最短路
1579: [Usaco2009 Feb]Revamping Trails 道路升级 Time Limit: 10 Sec Memory Limit: 64 MB Description 每天,农夫 ...
