JZOJ 5773. 【NOIP2008模拟】简单数学题

5773. 【NOIP2008模拟】简单数学题 
(File IO): input:math.in output:math.out

Time Limits: 1000 ms  Memory Limits: 262144 KB  Detailed Limits  

Goto ProblemSet

Description

      话说， 小X是个数学大佬，他喜欢做数学题。有一天，小X想考一考小Y。他问了小Y一道数学题。题目如下：
      对于一个正整数N，存在一个正整数T（0<T<N），使得
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAD4AAABECAYAAADZeIbjAAADRUlEQVR4nO2aMXKjMBSGf3ZyFG8KT04AJ7DduHKbTpROs11Kd2lwmXRpt6IJnMA+gceF4S5ayQYvBqEgGYF24ZuRCzPw+JH03pP0HMrAAPnR9wv0xSh8aNgnPPbhOA782KwZi4Sn2HoOnPlHJ9YsEj7BekdBkwBuB9YsEt4to/ChMQofGqPwoVEVnm7hscyJZ0+Ot2VpRfmyd7mWNdMZVj0x/MJ7iJuHbVlADq0jIny5SklUc80NaFJ7sx4RwdnmtclslN4hCVx2D6F/XzeiRHJ/rfCIuNR1xca5EeEH6ZCIFEUmNKi8a0SDoL5raoSzBwVR1usuvb2fGykatQHWu2yEuBKhZcTOLf3CET+B2RIEe7y8FSdywq5N+VV7iEPwpc3T46TxLWLhCTBd8IfM8IuNIXyEuEpnRg6rBZqbME96OrBfguWs+T1C4XF4RP7xJutX9sgPbDL3mJ6A1cIq2fj6vWczUm0UCoSnON0M5RmWbALtX95Yr3MjQN2Iiv3vwosDrza+6MKmHtetOgorsz4JKCk7Cfafew5tzIm07M4BNG5CZGFXQrXHk2O1SycLrPhUn89xmLbr1uglsjRqInTmd264gCRUCUNb31zCGDRG4VX4JfPJh5VIIPsopP1sTY8sYSlNBRX9Dv+5Y6T+s4yrMzvItpiv4c+HqcWfRcK56GfgM/fi0TlxmpsSb8j7qBMFVYea5Q8qi4+m2NPjszXW5dRr8ognQ+bsEV6La2RtYHc44weI4RL0XTUt+56H1p/YGszZbYBo175ojrXCY597+B3MyLZUON/JDZc7vBtc9lvn3LjoZ3yiOK3TrV+/TaxL6wHyDm4XSg23mTWxRnhlT73QTCQwdoczg1g3x7vi7NX5Suh/pzywH0R/DoHBDvVR+NAYhTei82qJO6seZGilPV1VS9xZ9SBDa6jH4QEuP1LaCHr9dAB5XbdyjByHfD2eP0t8KjrVPbJW/1Z9VUuoVz3IUO/xvqolNKoeZKgL76laQvtUtAZl4f1US+hVPchQFN5XtYRm1YMMJY/QcbXEFc2qBxlqPd5xtURO2/P7TPNv1Fe1hH7Vg4xGwvuplri/6kHGuOc2NEbhQ2MUPjRG4UPjD4ped/B8yB0SAAAAAElFTkSuQmCC" alt=" " />
的值是正整数。
      小X给出N，让小Y给出所有可能的T。如果小Y不回答这个神奇的大佬的简单数学题,他学神的形象就会支离破碎。所以小Y求你帮他回答小X的问题。

 

Input

      一个整数N。

Output

      第一个数M，表示对于正整数N，存在M个不同的正整数T，使得
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAD4AAABECAYAAADZeIbjAAADRUlEQVR4nO2aMXKjMBSGf3ZyFG8KT04AJ7DduHKbTpROs11Kd2lwmXRpt6IJnMA+gceF4S5ayQYvBqEgGYF24ZuRCzPw+JH03pP0HMrAAPnR9wv0xSh8aNgnPPbhOA782KwZi4Sn2HoOnPlHJ9YsEj7BekdBkwBuB9YsEt4to/ChMQofGqPwoVEVnm7hscyJZ0+Ot2VpRfmyd7mWNdMZVj0x/MJ7iJuHbVlADq0jIny5SklUc80NaFJ7sx4RwdnmtclslN4hCVx2D6F/XzeiRHJ/rfCIuNR1xca5EeEH6ZCIFEUmNKi8a0SDoL5raoSzBwVR1usuvb2fGykatQHWu2yEuBKhZcTOLf3CET+B2RIEe7y8FSdywq5N+VV7iEPwpc3T46TxLWLhCTBd8IfM8IuNIXyEuEpnRg6rBZqbME96OrBfguWs+T1C4XF4RP7xJutX9sgPbDL3mJ6A1cIq2fj6vWczUm0UCoSnON0M5RmWbALtX95Yr3MjQN2Iiv3vwosDrza+6MKmHtetOgorsz4JKCk7Cfafew5tzIm07M4BNG5CZGFXQrXHk2O1SycLrPhUn89xmLbr1uglsjRqInTmd264gCRUCUNb31zCGDRG4VX4JfPJh5VIIPsopP1sTY8sYSlNBRX9Dv+5Y6T+s4yrMzvItpiv4c+HqcWfRcK56GfgM/fi0TlxmpsSb8j7qBMFVYea5Q8qi4+m2NPjszXW5dRr8ognQ+bsEV6La2RtYHc44weI4RL0XTUt+56H1p/YGszZbYBo175ojrXCY597+B3MyLZUON/JDZc7vBtc9lvn3LjoZ3yiOK3TrV+/TaxL6wHyDm4XSg23mTWxRnhlT73QTCQwdoczg1g3x7vi7NX5Suh/pzywH0R/DoHBDvVR+NAYhTei82qJO6seZGilPV1VS9xZ9SBDa6jH4QEuP1LaCHr9dAB5XbdyjByHfD2eP0t8KjrVPbJW/1Z9VUuoVz3IUO/xvqolNKoeZKgL76laQvtUtAZl4f1US+hVPchQFN5XtYRm1YMMJY/QcbXEFc2qBxlqPd5xtURO2/P7TPNv1Fe1hH7Vg4xGwvuplri/6kHGuOc2NEbhQ2MUPjRG4UPjD4ped/B8yB0SAAAAAElFTkSuQmCC" alt=" " />
是整数。
后面是M个数，每一个数代表可能的正整数T（按从小到大的顺序排列）。

 

Sample Input

Sample Input1:
1

Sample Input2:
3

Sample Input3
180

Sample Output

Sample Output
0

Sample Output
1 2

Sample Output
5 120 144 160 168 176

 

 

Data Constraint

      对于5%的数据，N=1.
      对于20%的数据，N<=5.
      对于40%的数据，N<=1000000
      对于另外20%的数据，答案只有1个，且N为质数，保证对于前60%的数据，当N为质数的时候，答案都一定只有一个,对于这20%的数据，满足2<N。
      对于80%的数据，N<=10^9.
      对于100%的数据，N<=10^14.

 

做法：经过一系列推导，

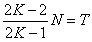也就是说,我们要使 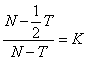是一个正整数,那么我们只需要让是的(奇数)因数(当然1是不能算的)。

那么，答案为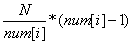，(其中（num[i]）为N的因子)

代码如下：

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #include <cmath>
 #define LL long long
 #define N 1000007
 using namespace std;
 LL n;
 LL num[N], ans;

 int main()
 {
     freopen("math.in", "r", stdin);
     freopen("math.out", "w", stdout);
     scanf("%lld", &n);
     if (n > )
     {
         LL p = sqrt(n);
         for (int i = ; i <= p + ; i++)
             if (n % i == )
             {
                 if (i %  !=  && i != )    num[++ans] = i;
                 if ((n / i) %  != )
                     num[++ans] = n / i;
             }
         if (n % p == )    num[ans--] = ;
         sort(num + , num + ans + );
         printf("%lld ", ans);
         for (int i = ; i <= ans; i++)
         {
             LL g = n / num[i];
             printf("%lld ", g * (num[i] - ));
         }
     }
     else
     {
         if (n == )
             printf("1 2");
         else if (n == )
             printf("1 4");
         else printf("");
     }
 }