简单易学的机器学习算法——基于密度的聚类算法DBSCAN

一、基于密度的聚类算法的概述

    最近在Science上的一篇基于密度的聚类算法《Clustering by fast search and find of density peaks》引起了大家的关注(在我的博文“论文中的机器学习算法——基于密度峰值的聚类算法”中也进行了中文的描述)。于是我就想了解下基于密度的聚类算法，熟悉下基于密度的聚类算法与基于距离的聚类算法，如K-Means算法之间的区别。

    基于密度的聚类算法主要的目标是寻找被低密度区域分离的高密度区域。与基于距离的聚类算法不同的是，基于距离的聚类算法的聚类结果是球状的簇，而基于密度的聚类算法可以发现任意形状的聚类，这对于带有噪音点的数据起着重要的作用。

二、DBSCAN算法的原理

1、基本概念

    DBSCAN(Density-Based Spatial Clustering of Application with Noise)是一种典型的基于密度的聚类算法，在DBSCAN算法中将数据点分为一下三类：

• 核心点。在半径Eps内含有超过MinPts数目的点
• 边界点。在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内
• 噪音点。既不是核心点也不是边界点的点

在这里有两个量，一个是半径Eps，另一个是指定的数目MinPts。

    一些其他的概念

1. Eps邻域。简单来讲就是与点的距离小于等于Eps的所有的点的集合，可以表示为。
2. 直接密度可达。如果在核心对象的Eps邻域内，则称对象从对象出发是直接密度可达的。
3. 密度可达。对于对象链：，是从关于Eps和MinPts直接密度可达的，则对象是从对象关于Eps和MinPts密度可达的。

2、算法流程

(流程)

三、实验仿真

    在实验中使用了两个测试数据集，数据集的原始图像如下：

(数据集1)

(数据集2)

数据集1相对比较简单。显然我们可以发现数据集1共有两个类，数据集2有四个类，下面我们通过DBSCAN算法实现数据点的聚类：

 

MATLAB代码

主程序

 

 

1. %% DBSCAN
2. clear all;
3. clc;
4. %% 导入数据集
5. % data = load('testData.txt');
6. data = load('testData_2.txt');
7. % 定义参数Eps和MinPts
8. MinPts = 5;
9. Eps = epsilon(data, MinPts);
10. [m,n] = size(data);%得到数据的大小
11. x = [(1:m)' data];
12. [m,n] = size(x);%重新计算数据集的大小
13. types = zeros(1,m);%用于区分核心点1，边界点0和噪音点-1
14. dealed = zeros(m,1);%用于判断该点是否处理过,0表示未处理过
15. dis = calDistance(x(:,2:n));
16. number = 1;%用于标记类
17. %% 对每一个点进行处理
18. for i = 1:m
19. %找到未处理的点
20. if dealed(i) == 0
21. xTemp = x(i,:);
22. D = dis(i,:);%取得第i个点到其他所有点的距离
23. ind = find(D<=Eps);%找到半径Eps内的所有点
24. %% 区分点的类型
25. %边界点
26. if length(ind) > 1 && length(ind) < MinPts+1
27. types(i) = 0;
28. class(i) = 0;
29. end
30. %噪音点
31. if length(ind) == 1
32. types(i) = -1;
33. class(i) = -1;
34. dealed(i) = 1;
35. end
36. %核心点(此处是关键步骤)
37. if length(ind) >= MinPts+1
38. types(xTemp(1,1)) = 1;
39. class(ind) = number;
40. % 判断核心点是否密度可达
41. while ~isempty(ind)
42. yTemp = x(ind(1),:);
43. dealed(ind(1)) = 1;
44. ind(1) = [];
45. D = dis(yTemp(1,1),:);%找到与ind(1)之间的距离
46. ind_1 = find(D<=Eps);
47. if length(ind_1)>1%处理非噪音点
48. class(ind_1) = number;
49. if length(ind_1) >= MinPts+1
50. types(yTemp(1,1)) = 1;
51. else
52. types(yTemp(1,1)) = 0;
53. end
54. for j=1:length(ind_1)
55. if dealed(ind_1(j)) == 0
56. dealed(ind_1(j)) = 1;
57. ind=[ind ind_1(j)];
58. class(ind_1(j))=number;
59. end
60. end
61. end
62. end
63. number = number + 1;
64. end
65. end
66. end
67. % 最后处理所有未分类的点为噪音点
68. ind_2 = find(class==0);
69. class(ind_2) = -1;
70. types(ind_2) = -1;
71. %% 画出最终的聚类图
72. hold on
73. for i = 1:m
74. if class(i) == -1
75. plot(data(i,1),data(i,2),'.r');
76. elseif class(i) == 1
77. if types(i) == 1
78. plot(data(i,1),data(i,2),'+b');
79. else
80. plot(data(i,1),data(i,2),'.b');
81. end
82. elseif class(i) == 2
83. if types(i) == 1
84. plot(data(i,1),data(i,2),'+g');
85. else
86. plot(data(i,1),data(i,2),'.g');
87. end
88. elseif class(i) == 3
89. if types(i) == 1
90. plot(data(i,1),data(i,2),'+c');
91. else
92. plot(data(i,1),data(i,2),'.c');
93. end
94. else
95. if types(i) == 1
96. plot(data(i,1),data(i,2),'+k');
97. else
98. plot(data(i,1),data(i,2),'.k');
99. end
100. end
101. end
102. hold off

 

距离计算函数

1. %% 计算矩阵中点与点之间的距离
2. function [ dis ] = calDistance( x )
3. [m,n] = size(x);
4. dis = zeros(m,m);
5. for i = 1:m
6. for j = i:m
7. %计算点i和点j之间的欧式距离
8. tmp =0;
9. for k = 1:n
10. tmp = tmp+(x(i,k)-x(j,k)).^2;
11. end
12. dis(i,j) = sqrt(tmp);
13. dis(j,i) = dis(i,j);
14. end
15. end
16. end

epsilon函数

1. function [Eps]=epsilon(x,k)
2. % Function: [Eps]=epsilon(x,k)
3. %
4. % Aim:
5. % Analytical way of estimating neighborhood radius for DBSCAN
6. %
7. % Input:
8. % x - data matrix (m,n); m-objects, n-variables
9. % k - number of objects in a neighborhood of an object
10. % (minimal number of objects considered as a cluster)
11. [m,n]=size(x);
12. Eps=((prod(max(x)-min(x))*k*gamma(.5*n+1))/(m*sqrt(pi.^n))).^(1/n);

 

最终的结果

 

(数据集1的聚类结果)

(数据集2的聚类结果)

在上面的结果中，红色的点代表的是噪音点，点代表的是边界点，十字代表的是核心点。不同的颜色代表着不同的类。

 

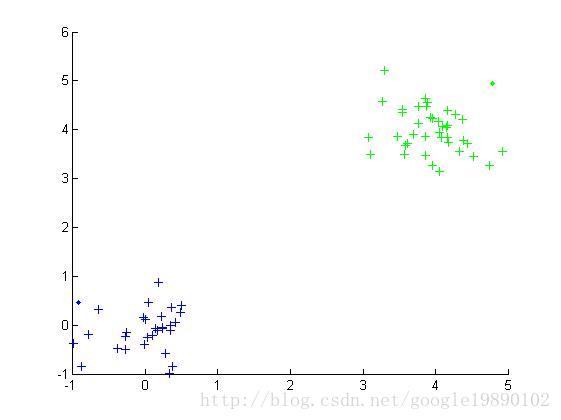
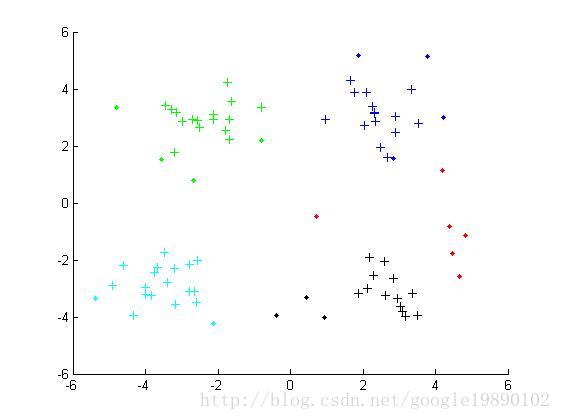
参考文献

[1] M. Ester, H. Kriegel, J. Sander, X. Xu, A density-based algorithm for discovering clusters in large spatial databases with noise,  www.dbs.informatik.uni-muenchen.de/cgi-bin/papers?query=--CO
[2] M. Daszykowski, B. Walczak, D. L. Massart, Looking for Natural Patterns in Data. Part 1: Density Based Approach