FZU - 2295 Human life:网络流-最大权闭合子图-二进制优化-第九届福建省大学生程序设计竞赛

（有任何问题欢迎留言或私聊 && 欢迎交流讨论哦



http://acm.fzu.edu.cn/problem.php?pid=2295

http://acm.fzu.edu.cn/problem.php?pid=2295

Catalog

目录

• Catalog
  • Problem：Portal传送门
• Solution：
  • AC_Code：

Problem：Portal传送门

 原题目描述在最下面。

 题意就是很裸的最大权闭合子图。

 推荐阅读：胡伯涛《最小割模型在信息学竞赛中的应用》

 完完全全的模板题：新疆大学五月月赛-D-勤奋的杨老师

 本题题意：m(50)个任务，n个技能。完成每个任务由相应的收益，完成每个任务前必须学一些技能。有些技能由先修技能。

 有些任务不能同时完成。

Solution：

 训练赛的时候听队友讲完题意，一眼就直接建对图了，但是没敢敲，因为比赛刚开始，想先写签到题。

 详细de题解啊啊啊

 直接讲建图：源点S想每个任务连边，流量为其收益，每个任务向其需要的技能连边，每个任务向先修技能连边，每个技能向汇点T连边，流量为其花费。答案是\(sum_{任务}-maxflow\).

 难点在于有些任务不能同时完成。因为只有k(5)对，直接二进制枚举所有对互斥情况。为1则不能选第一个任务，为0则不能选第二个任务。不选就是取反再异或一下。

 细节看代码吧。

AC_Code：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#define mme(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;

const int MXN = 2e2+7;
const int MXE = MXN*MXN;
struct DINIC{
  int tot,vt,vs;
  int d[MXN],head[MXN];
  struct lp{
    int v,w,nex;
  }cw[MXE];
  void add_edge(int a,int b,int c){
    cw[++tot].v=b;cw[tot].nex=head[a],cw[tot].w=c;
    head[a]=tot;
    cw[++tot].v=a;cw[tot].nex=head[b],cw[tot].w=0;
    head[b]=tot;
  }
  bool bfs(){
    memset(d,-1,sizeof(d));
    queue<int>Q;
    Q.push(vt);d[vt]=0;
    while(!Q.empty()){
      int u=Q.front();
      Q.pop();
      for(int i=head[u];i!=-1;i=cw[i].nex){
        int v=cw[i].v;
        if(cw[i^1].w&&d[v]==-1){
          d[v]=d[u]+1;
          Q.push(v);
        }
      }
    }
    return d[vs]!=-1;
  }
  int dfs(int x,int f){
    if(x==vt||f==0) return f;
    int use=0,w;
    for(int i=head[x];i!=-1;i=cw[i].nex){
      int to=cw[i].v;
      if(d[to]==d[x]-1 && cw[i].w){
        w=dfs(to,min(cw[i].w,f-use));
        cw[i].w-=w,cw[i^1].w+=w;
        use+=w;
        if(use==f) return f;
      }
    }
    return use;
  }
  void init(int st,int ed){
    tot = -1;
    memset(head,-1,sizeof(head));
    vs = st; vt = ed;
  }
  int max_flow(){
    int ans=0;
    while(bfs())ans+=dfs(vs,INF);
    return ans;
  }
}dinic;
const int N = 105;
int n, m, k;
int vs, vt;
struct lp{
  int v,x;
  int a[N];
}ar[N],br[N];
int c[N],d[N];
int main(){
  int tim;
  scanf("%d", &tim);
  while(tim--){
    scanf("%d%d%d", &n, &m, &k);
    vs = 0;vt = m+n+1;
    for(int i = 1; i <= n; ++i){
      int v,x;
      scanf("%d%d", &v, &x);
      ar[i].v=v;ar[i].x=x;
      for(int j = 0; j < x; ++j){
        scanf("%d", &ar[i].a[j]);
      }
    }
    for(int i = 1; i <= m; ++i){
      int v,x;
      scanf("%d%d", &v, &x);
      br[i].v=v;br[i].x=x;
      for(int j = 0; j < x; ++j){
        scanf("%d", &br[i].a[j]);
      }
    }
    for(int i = 0; i < k; ++i){
      scanf("%d%d", &c[i], &d[i]);
      --c[i];--d[i];
    }
    int sta = 1 << k, ans = 0;
    //printf("%lld\n", 1<<50);
    for(int t = 0; t < sta; ++t){
      LL hhh = (1LL<<m)-1;
      for(int i = 0; i < k; ++i){
        LL x = 1LL<<c[i], y = 1LL<<d[i];
        if(t&(1<<i)){
          hhh &= (~x);
        }else{
          hhh &= (~y);
        }
      }
      //printf("hhh = %d\n", hhh);
      dinic.init(vs, vt);
      for(int i = 1, v; i <= n; ++i){
        dinic.add_edge(i+m,vt,ar[i].v);
        for(int j = 0; j < ar[i].x; ++j){
          v = ar[i].a[j];
          dinic.add_edge(i+m,v+m,INF);
        }
      }
      int sum = 0, tmp;
      for(int i = 1, v; i <= m; ++i){
        if((hhh&(1LL<<(i-1)))==0)continue;
        dinic.add_edge(vs,i,br[i].v);
        sum += br[i].v;
        for(int j = 0; j < br[i].x; ++j){
          v = br[i].a[j];
          dinic.add_edge(i,v+m,INF);
        }
      }
      tmp = dinic.max_flow();
      ans = max(ans, sum - tmp);
    }
    printf("%d\n", ans);
  }
  return 0;
}

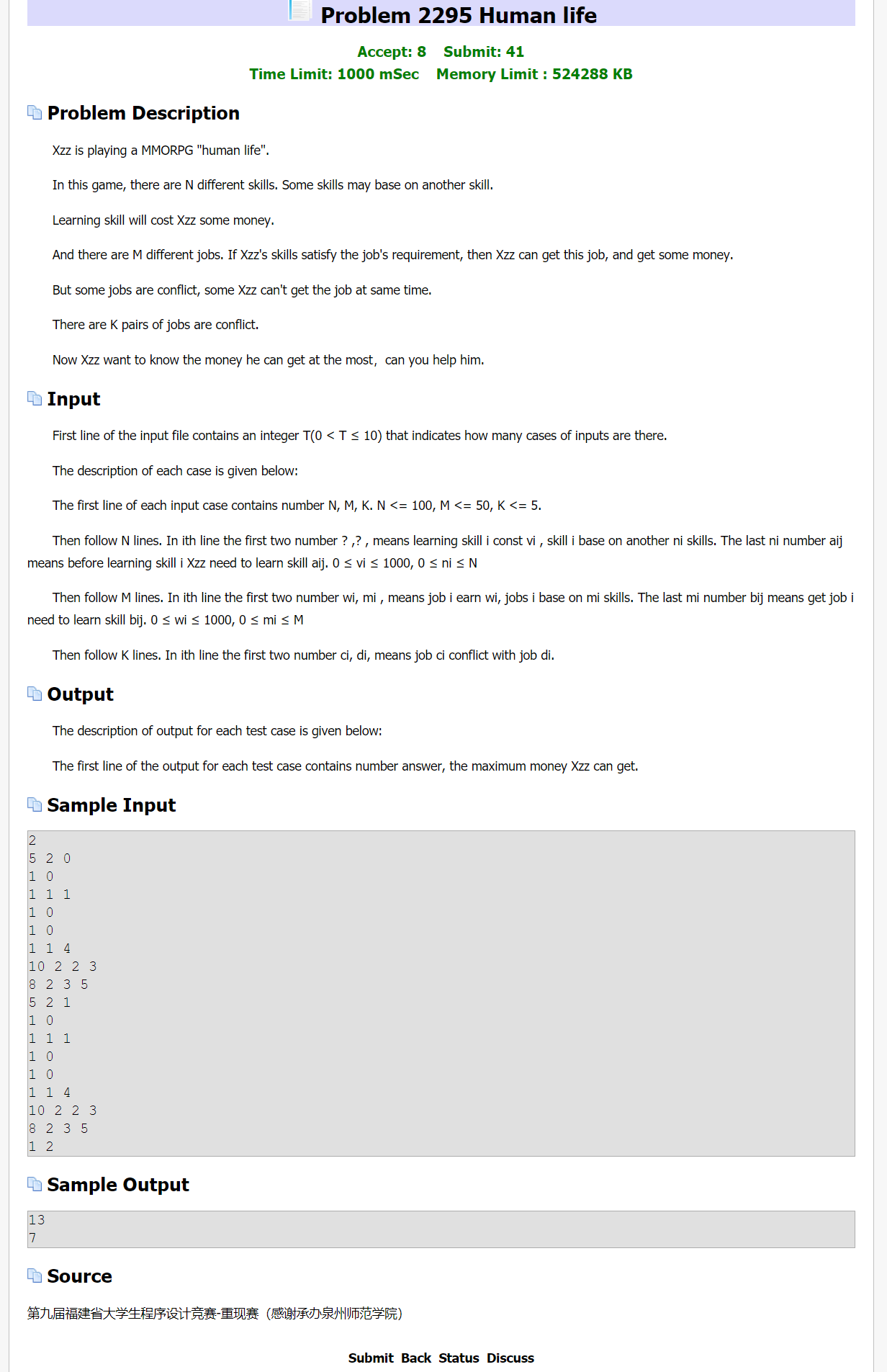
####Problem Description：