E - D Tree HDU - 4812 点分治+逆元

这道题非常巧妙！！！

我们进行点分治的时候，算出当前子节点的所有子树中的节点，到当前节点节点的儿子节点的距离，如下图意思就是

当前节点的红色节点，我们要求出红色节点的儿子节点绿色节点，所有绿色的子树节点的到当绿色的点权乘积

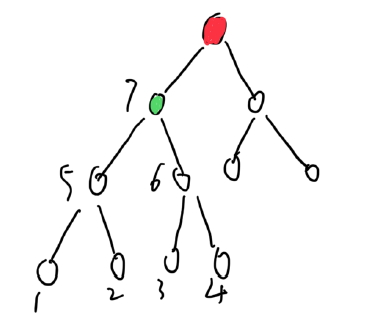
有如下的情况：

1*5*7  3*6*7

2*5*7 4*6*7

然后我们要想办法查询其他链上到红色节点的乘积，比如蓝色的所有子树到红色节点的乘积，以及这些乘积对应的链的尾部节点。

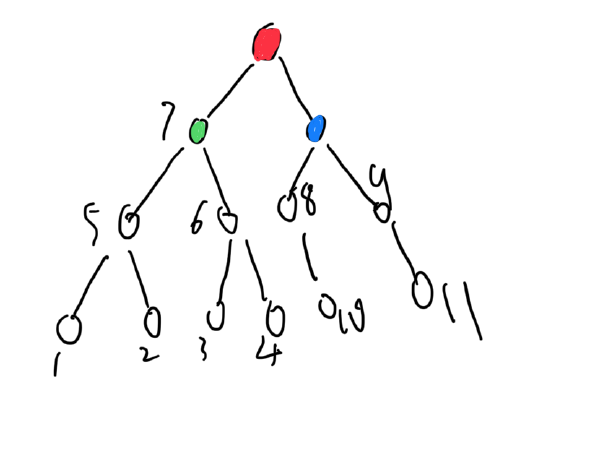
因此我们需要用逆元求，因为我们并不容易直接求出一条链上所有节点的点权乘积为K的链，但是我们可以通过搜索出所有当前节点的乘积，然后查询逆元长度的链条是否存在，更加方便的求出答案。

比较抽象。。。多打几遍就懂了。。。

#pragma comment(linker,"/STACK:102400000,102400000")
#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<string.h>
#define LL long long
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxx = 2e5+6;
const int MOD = 1000003;
int ver[maxx],head[maxx],Next[maxx],q[maxx];
int sz[maxx],mp[MOD+10],vis[maxx],a[maxx],id[maxx];
int inv[MOD+10];
int tot,mx,size,root,l,r,ansx,ansy,k;
inline int read()
{
    int x=0;char ch=getchar();
    while(ch<'0'||ch>'9')ch=getchar();
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x;
}
void add(int u,int v){
   ver[++tot]=v;Next[tot]=head[u];head[u]=tot;
   ver[++tot]=u;Next[tot]=head[v];head[v]=tot;
}
///求重心
void getroot(int u,int fa){
     sz[u]=1;
     int num=0;
     for (int i=head[u];i;i=Next[i]){
        int v=ver[i];
        if (v==fa||vis[v])continue;
        getroot(v,u);
        sz[u]+=sz[v];
        num=max(num,sz[v]);
     }
     num=max(num,size-sz[u]);
     if (num<mx)mx=num,root=u;
}
///求子树的链的点权积
void getdis(int u,int fa,int val){
    q[++r]=val;
    id[r]=u;
    for (int i=head[u];i;i=Next[i]){
        int v=ver[i];
        if (v==fa || vis[v])continue;
        getdis(v,u,(LL)val*a[v]%MOD);
    }
}
///检查逆元所对应的长度是否存在
void check(int x,int val){
   int w=(LL)inv[val]*k%MOD;
   int y=mp[w];
   if (y==0||x==y)return;
   if (x>y)swap(x,y);
   if (x<ansx || (x==ansx && y<ansy)){
      ansx=x;
      ansy=y;
   }
   return;
}
void solve(int u){
    vis[u]=1;
    mp[a[u]]=u;
    ///求出当前节点的子树对应的点权积
    for (int i=head[u];i;i=Next[i]){
        int v=ver[i];
        if (vis[v])continue;
        r=0;
        getdis(v,u,a[v]);
        for (int j=1;j<=r;j++){
            check(id[j],q[j]);
        }
        ///把所有子树链的乘积再乘上当前节点的权值，
        ///这样保存使得另外一颗子树的一条链能够轻松找到另外一条不和自己在同一个子树内且点权乘积为K的长度
        for (int j=1;j<=r;j++){
            q[j]=(LL)q[j]*a[u]%MOD;
            int now=mp[q[j]];
            if (now==0 || now>id[j]){
                mp[q[j]]=id[j];
            }
        }
    }
    mp[a[u]]=0;
    ///要继续点分治，父亲节点的信息以及没有用了
    for (int i=head[u];i;i=Next[i]){
        int v=ver[i];
        if(vis[v])continue;
        r=0;
        l=1;
        getdis(v,u,(LL)a[u]*a[v]%MOD);
        for(int j=1;j<=r;j++){
            mp[q[j]]=0;
        }
    }
    for (int i=head[u];i;i=Next[i]){
        int v=ver[i];
        if (vis[v])continue;
        size=sz[v];
        mx=INF;
        getroot(v,0);
        solve(root);
    }
}
int main(){
  inv[1]=1;
  for (int i=2;i<MOD;i++){
     inv[i]=(LL)(MOD-(MOD/i))*inv[MOD%i]%MOD;
  }
  int n;
  while(~scanf("%d%d",&n,&k)){
     for(int i=1;i<=n;i++){
        a[i]=read();
     }
     tot=0;
     memset(mp,0,sizeof(mp));
     int u,v;
     for (int i=1;i<=n;i++){
        vis[i]=0;
        head[i]=0;
     }
     tot=0;
     for (int i=1;i<n;i++){
        u=read();
        v=read();
        add(u,v);
     }
     ansx=INF;
     ansy=INF;
     mx=INF;
     size=n;
     getroot(1,0);
     solve(root);
     if (ansx==INF){
        printf("No solution\n");
     }else {
        printf("%d %d\n",ansx,ansy);
     }
  }
  return 0;
}